引入
提升树 (Tree boosting)是一种高效的集成学习方法。在这篇文章中,作者陈天奇等人提出了一个可伸缩的、端到端的提升树系统,也就是XGBoost。XGBoost在很多机器学习领域的挑战性任务中取得了最好的效果 (state of art)。此外,他们分别提出了基于稀疏数据的稀疏优化算法,以及用于近似树学习的weighted quantile sketch方法。更重要的是,他们在缓存机制、数据压缩和分块上进行研究,使得XGBoost成为可伸缩的算法软件包。
本文的目的是对论文的前半部分,也就是XGBoost中的基础算法进行解读。
关于GBDT
梯度提升树 (Gradient Boosting Decision Tree, GBDT)是借助序列化的基模型(决策树回归器)对损失函数进行梯度下降,从而对模型进行优化。XGBoost其实就是对GBDT模型的高效实现,因此了解GBDT是必要的,建议读者阅读:
我们从实验中发现GBDT模型会有比较严重的过拟合问题。
XGBoost中的提升树
给定训练数据集$D=\{\pmb x_i,y_i\}_{i=1}^n$,$\pmb x_i\in\mathcal{R}^m$,$y_i\in\mathcal{R}$,一个提升树模型预测可以这样表示(加法模型)
\[\hat y_i=\phi(\pmb x_i)=\sum_{k=1}^Kf_k(\pmb x_i),\quad f_k\in\mathcal{F}\]其中$\mathcal F=\{f(\pmb x)=w_{q(\pmb x)}\}(q:\mathcal{R}^m\to T,w\in\mathcal{R}^T)$是一个回归树(CART)模型空间,$q$是一个函数,输入是训练数据,输出是该数据会落到的节点。$T$是叶节点数。每个$f_k$对应这一个树结构,而$w$是叶节点权重,也就是叶节点对应的值。我们举一个例子:
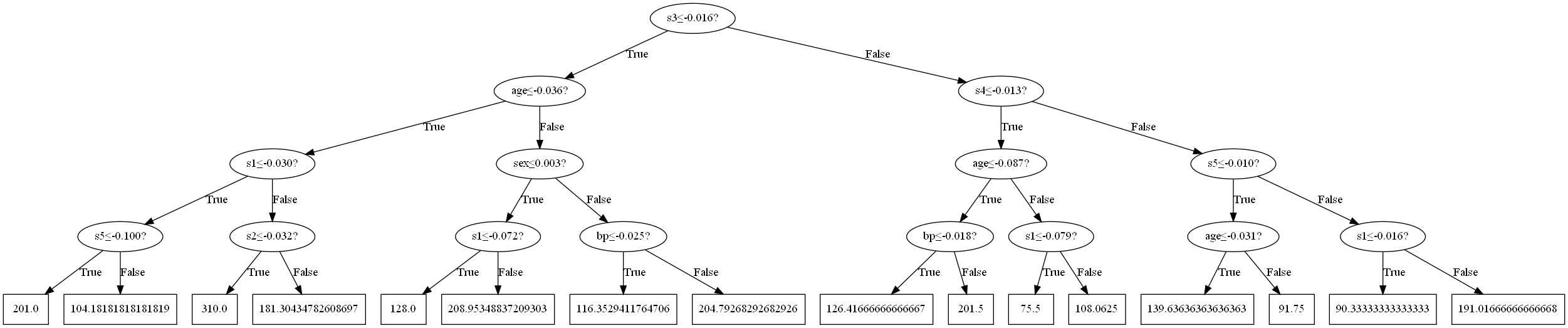
在该决策回归树中,一共16个节点,即$T=16$,假设在训练过程中,$\pmb x_1$落到了第一个叶节点,$\pmb x_2$落到了第三个叶节点。那么
\[\begin{aligned} f(\pmb x_1)&=w_{q(\pmb x_1)}=w_1=201.0\\ f(\pmb x_2)&=w_{q(\pmb x_2)}=w_3=310.0\\ \end{aligned}\]XGBoost考虑下面的优化目标(结构风险最小化)
\[\mathcal L(\phi)=\sum_{i}l(\hat{y}_i,y_i)+\sum_{k}\Omega(f_k)\\ \text{where}\quad\Omega(f)=\gamma T+\frac12\lambda\Vert w\Vert^2\tag1\]$l$是可微的凸损失函数,对预测值$\hat{y}_i$和标签$y_i$的差距进行度量;后面一项对应$k$个回归树的模型复杂度,通过叶节点个数和权重进行度量。
显然(1)是无法用基本方法优化的,因此考虑加法模型的方式求解。对第$t$轮迭代,我们需要将模型$f_t$加到原模型上,此时优化目标就是
\[\min_{f_t}\quad \mathcal{L}^{(t)}=\sum_{i=1}^nl(y_i,\hat{y}_i^{(t-1)}+f_t(\pmb x_i))+\Omega(f_t)\tag2\]考虑损失函数的二阶展开:
\[\mathcal{L}^{(t)}\simeq\sum_{i=1}^n[l(y_i,\hat{y}^{(t-1)})+g_if_t(\pmb x_i)+\frac12h_if_t^2(\pmb x_i)]+\Omega(f_t)\tag3\]其中
\[\begin{aligned} g_i&=\dfrac{\partial l(y_i,\hat{y}^{(t-1)})}{\partial\hat{y}^{(t-1)}}\\ h_i&=\dfrac{\partial^2l(y_i,\hat{y}^{(t-1)})}{\partial\hat{y}^{(t-1)^2}}\\ \end{aligned}\]也就是一阶和二阶导数。因此优化目标变成(4)式:
\[\min_{f_t}\quad \mathcal{L}^{(t)}=\sum_{i=1}^n[g_if_t(\pmb x_i)+\frac12h_if_t^2(\pmb x_i)]+\Omega(f_t)\tag4\]决策树的模型特性就是,在同一个叶节点的样本,它们的$f_t(\pmb x)$及其一阶和二阶导数都是相等的。定义$I_j={i\vert q(\pmb x_i)=j}$,也就是落在叶节点$j$的所有样本点索引,从而将(4)改写:
\[\min_{f_t}\quad\mathcal{L}^{(t)}=\sum_{j=1}^T[(\sum_{i\in I_j}g_i)w_j+\frac12(\sum_{i\in I_j}h_i+\lambda)w_j^2]+\gamma T\tag5\]也就是把对样本求和改为对决策树叶节点进行求和。显然(5)是多个不相关的二次模型的和,每个叶节点的最优权值存在闭式解:
\[w_j^*=-\dfrac{\sum_{i\in I_j}g_i}{\sum_{i\in I_j}h_i+\lambda}\tag6\]从而得到决策树$q$的最优损失:
\[\tilde{\mathcal{L}}(q)=-\frac12\sum_{j=1}^T\dfrac{(\sum_{i\in I_j}g_i)^2}{\sum_{i\in I_j}h_i+\lambda}+\gamma T\tag7\]上式可作为对决策树$q$的评估函数,该数值只和决策树的结构相关。因此就有一种贪心地构建提升树的方法,从一个节点开始,递归得产生左右两个叶节点,设$I_L,I_R$分别是分别落在左右两个叶节点的样本,令$I=I_L\cup I_R$,因此我们想找到一种分割方式,即阈值,使分割的结构风险最小化:
\[\mathcal{L}_{\text{split}}=\dfrac12\bigg[ \dfrac{(\sum_{i\in I_L}g_i)^2}{\sum_{i\in I_L}h_i+\lambda}+ \dfrac{(\sum_{i\in I_R}g_i)^2}{\sum_{i\in I_R}h_i+\lambda}-\dfrac{(\sum_{i\in I}g_i)^2}{\sum_{i\in I}h_i+\lambda} \bigg]-\gamma\tag8\]防止过拟合
除了优化目标中的正则化项,XGBoost还使用了两种技术来防止过拟合:
-
收缩(Shrinkage),由Friedman提出。收缩指对每一步提升加上一个系数$\eta$,也就是
\[F_n=F_{n-1}+\eta f_t\tag9\]$\eta$类似于梯度下降法中的学习率。
-
特征子采样(Column Subsampling),该方法也被应用在随机森林中,就是训练一棵树时随机选择部分特征作为输入。这样也能达到抑制过拟合的目的。
分割算法
树学习最重要的一点就是,给定某一个特征,如何找到一个阈值作为决策树分支的划分。本文提出了三种方法,分别是精确贪心算法、近似算法、加权分位数略图和稀疏感知分割。
精确贪心算法
其实和普通的连续变量决策树的划分算法类似,就是找到能最优化某一判别准则(比如离散分类树尝试最小化基尼指数,连续回归树尝试最小化左右子树MSE的和)。这里就是最小化(8)式,算法如下:

当然,我们需要先对样本点在该特征上的值进行排序,依次计算判断。
近似算法
不可否认精准贪心算法是很强的,但在数据量极大的情况下,数据无法完全纳入内存,此时遍历所有可能点是不现实的。在分布式训练中也会出现这样的问题。因此我们需要近似算法来避免该问题。
总的来说,算法先依据特征分布的分位点生成候选分割点, 然后将连续特征映射到根据候选点划分的桶中(类比桶排序),并对统计数据(梯度和二阶导数)进行求和,在此基础上找到最优方案:

比如样本在特征$k$上的取值排序后为
\[[1,4,6,7,7,9,9,11,11]\]当$l=2$,就是研究下面2种分割
\[[1,4,6], [7,7,9,9,11,11]; [1,4,6,7,7,9], [9,11,11]\\\]与不分割相比,哪种会最小化(8)式。
加权分位数略图
该方法是对上述近似算法的改进。上面提到的近似算法“依据特征分布的分位点生成候选分割点”,这样的分裂候选点的生成是均匀的。定义集合$\mathcal D_k=\{(x_{ik},h_i)\}_{i=1}^n$为数据集中数据第$k$个特征值和对应的二阶导数。然后作者定义了一个排名函数$r_k:\mathcal{R}\to\mathcal{R}^+$
\[r_k(z)=\dfrac{1}{\sum_{(x,h)\in\mathcal D_k}h}\sum_{(x,h)\in\mathcal D_k,x<z}h\tag{10}\]也就是特征值小于$z$的样本对应的二阶梯度和与整体二阶梯度和的比值。这样做的目标是找到候选分割点$\{s_{k1},s_{k2},\cdots,s_{kl}\}$使得
\[\vert{r_k(s_{k,j})-r_k(s_{k,j+1})}\vert<\epsilon,s_{k1}=\min_i\pmb x_{ik},s_{kl}=\max_i\pmb x_{ik}\tag{11}\]这里$\epsilon$就是近似系数,说明大概有$1/\epsilon$个候选点。显然数据的权值是用$h_i$,也就是二阶梯度来衡量,这是因为(4)式可改写为
\[\min_{f_t}\quad \mathcal{L}^{(t)}=\sum_{i=1}^n\frac12h_i(f_t(\pmb x_i)-\dfrac{g_i}{h_i})^2+\Omega(f_t)\tag4\]可以发现优化目标的前面等价于最小化带权平方损失,标签为$g_i/h_i$,样本权重为$h_i$。
稀疏感知分割
在现实问题中,输入$\pmb x$稀疏是挺正常的事情,导致数据稀疏的原因:
- 缺失值;
- 统计数据中频繁的零项;
- 特征工程,比如one-hot编码。
XGBoost针对第一种情况,在树中加入“默认方向”,一旦特征值缺失,那么节点就会按照默认方向落入左子树或右子树。这种默认方向是从训练数据里学出来的,具体算法如下:

可以看出,面对缺失值,算法会将它分别放入左子树和右子树算出最优分割,然后进行比较后确定最终的默认方向。
总结
这里我们总结了XGBoost论文中最主要的算法部分,包括带正则化的梯度提升树的优化目标形式化,以及如何训练其中的决策树。论文的后半部分则是对XGBoost实现亮点的介绍,我们会在后面的文章里补充。