在从残差逼近到GBDT中,我们说到用GBDT方法将弱回归器集成为强回归器。但我们是否能将该方法应用到分类中呢,答案是肯定的。本文的目的便是将残差逼近与GBDT的方法拓展到分类问题上来。
二分类情形
我们这里进行一段不是很严谨的推理。考虑线性回归模型:
\[y=\pmb w^T\pmb x+b\tag{1}\]与之对应的线性二分类模型是对率回归模型:
\[p(y=1\vert\pmb x)=\dfrac1{1+\exp(-(\pmb w^T\pmb x+b))}\tag{2}\]回归模型下,我们希望(1)更贴近训练数据;分类模型下,我们希望(2)更贴近训练数据。实际上都是对参数$\pmb w$和$b$的训练,更进一步,都是对$\pmb w^T\pmb x+b$的训练。因此迁移到梯度提升模型,回归模型想要训练更贴近训练集的加法模型
\[F_{n}=\sum_{i=1}^nf_i\tag3\]因此在二分类场景中,我们想训练更贴近训练集的模型
\[p(y=1\vert\pmb x)=\dfrac1{1+\exp(-F_n(\pmb x))}\tag4\]实际上$F_n(\pmb x)$对应的就是对率 (logit):$\ln\frac{p}{1-p}$。考虑此时二分类的交叉熵损失
\[\begin{aligned} l(y,\hat{y})&=-y\log(\hat{y})-(1-y)\log(1-\hat{y})\\ &=y\log(1+e^{-F_n(\pmb x)})+(1-y)(F_n(\pmb x)+\log(1+e^{-F_n(\pmb x)}))\\ \dfrac{\partial l}{\partial F_n(\pmb x)}&=y-\dfrac1{1+e^{-F_n(\pmb x)}}\\ &=y-\hat{y} \end{aligned}\tag5\]因此和前面的回归问题一样,我们在分类问题中对残差的逼近 (这里的残差是概率上的),等价于对交叉熵进行梯度下降。
下面是笔者编写的二分类梯度提升Python程序(仿sklearn接口),我们用深度为5的回归树作为基模型。
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
class BoostBinaryClassifier:
def __init__(
self,
base_model=DecisionTreeRegressor,
params={"max_depth": 5},
T=10,
) -> None:
self.T = T
self.base_model = base_model
self.boost_model = [self.base_model(**params) for _ in range(self.T)]
def fit(self, X, y):
p1 = np.sum(y == 1) / len(y)
self.logit = np.log(p1 / (1 - p1))
# 这里以先验对率作为第一个模型,而不是全0
pred = self.logit * np.ones(y.shape)
for i in range(self.T):
y_hat = 1 / (1 + np.exp(-pred))
self.boost_model[i].fit(X, y - y_hat)
pred += self.boost_model[i].predict(X)
return self
def predict(self, X):
pred = self.logit * np.ones(X.shape[0])
for model in self.boost_model:
pred += model.predict(X)
return (pred >= 0).astype(int)
def score(self, X, y):
pred = self.predict(X)
return accuracy_score(y, pred)
if __name__ == "__main__":
X, y = load_breast_cancer(return_X_y=True)
train_X, test_X, train_y, test_y = train_test_split(
X,
y,
train_size=0.7,
random_state=42,
)
clf = BoostBinaryClassifier()
clf.fit(train_X, train_y)
print("train accuracy : {:.2f}, test accuracy : {:.2f}".format(
clf.score(train_X, train_y),
clf.score(test_X, test_y),
))
得到训练准确率为100%,同时测试准确率为96%,相比于使用相同深度的决策树分类只能实现95%的准确率。我们绘制100轮迭代中,模型的训练和测试的交叉熵损失和准确率图像:
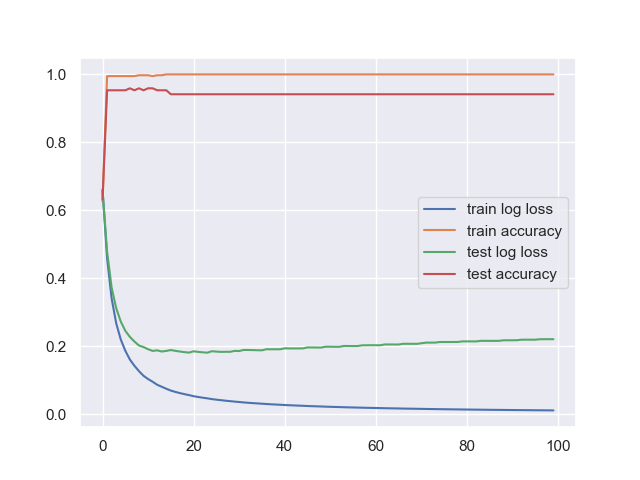
能够看到在第10轮迭代附近,模型就会发生过拟合,同时体现在准确率和损失上。
多分类情形
考虑我们是如何将对率回归的二分类拓展成$k$分类的($k\geq3$)。考虑下面的Softmax模型
\[\begin{aligned} p(y=1\vert\pmb x)&=\dfrac{e^{\pmb w_1^T\pmb x}}{\sum_{i=1}^ke^{\pmb w_i^T\pmb x}}\\ p(y=2\vert\pmb x)&=\dfrac{e^{\pmb w_2^T\pmb x}}{\sum_{i=1}^ke^{\pmb w_i^T\pmb x}}\\ \cdots\\ p(y=k\vert\pmb x)&=\dfrac{e^{\pmb w_k^T\pmb x}}{\sum_{i=1}^ke^{\pmb w_i^T\pmb x}}\\ \end{aligned}\tag6\]因此,我们需要用到$k$组梯度提升模型,分别拟合$k$个softmax对应的对率,也就是
\[\begin{aligned} p(y=1\vert\pmb x)&=\dfrac{e^{F^1_n(\pmb x)}}{\sum_{i=1}^ke^{F^i_n(\pmb x)}}\\ p(y=2\vert\pmb x)&=\dfrac{e^{F^2_n(\pmb x)}}{\sum_{i=1}^ke^{F^i_n(\pmb x)}}\\ \cdots\\ p(y=k\vert\pmb x)&=\dfrac{e^{F^k_n(\pmb x)}}{\sum_{i=1}^ke^{F^i_n(\pmb x)}}\\ \end{aligned}\tag7\]损失函数是多分类下的交叉熵损失
\[\begin{aligned} l(y,\hat{y}) &=-\sum_{i=1}^ky_i\log(\hat{y}_i)\\ &=-\sum_{i=1}^ky_i\log\bigg(\dfrac{e^{F_n^i(\pmb x)}}{\sum_{j=1}^k e^{F_n^j(\pmb x)}}\bigg)\\ &=-\sum_{i=1}^ky_i\bigg(F_n^i(\pmb x)-\log(\sum_{j=1}^ke^{F_n^j(\pmb x)})\bigg)\\ \end{aligned}\]此处$y$和$\hat{y}$都是$k$维向量,其中$y$是one-hot的,对应类别的位置为1。我们还是考虑损失函数对第$i$类的对率的梯度,不难求得
\[\begin{aligned} \dfrac{\partial l}{\partial F_n^i} &=y_i-\hat{y}_i \end{aligned}\]因此对多分类问题中的对率进行残差逼近,等价于交叉熵的梯度下降。
这个结论是很有用的,考虑损失函数为交叉熵函数,输出层为Softmax的神经网络,这一结论能够为神经网络的反向传播带来便利。
我们考虑Python实现该算法
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics import accuracy_score
from scipy.special import softmax
class BoostClassifier:
def __init__(
self,
base_model=DecisionTreeRegressor,
params={"max_depth": 5},
T=50,
) -> None:
self.T = T
self.base_model = base_model
self.params = params
def fit(self, X, y):
one_hot_y = OneHotEncoder(sparse=False).fit_transform(y.reshape(-1, 1))
dist = one_hot_y.sum(0) / len(y)
self.n_class = len(dist)
prior = dist / dist.sum()
self.boost_model = [[
self.base_model(**self.params) for _ in range(self.n_class)
] for __ in range(self.T)]
self.logit = np.log(prior / (1 - prior))
pred = self.logit * np.ones(one_hot_y.shape)
for t in range(self.T):
y_hat = softmax(pred, 1)
neg_grad = one_hot_y - y_hat
for i in range(self.n_class):
self.boost_model[t][i].fit(X, neg_grad[:, i])
pred[:, i] += self.boost_model[t][i].predict(X)
return self
def predict(self, X):
pred = self.logit * np.ones((X.shape[0], self.n_class))
for i in range(self.T):
pred += np.array([
self.boost_model[i][c].predict(X) for c in range(self.n_class)
]).T
return np.argmax(pred, 1)
def score(self, X, y):
pred = self.predict(X)
return accuracy_score(y, pred)
我们对sklearn自带额digits数据集采用最大深度为3的决策树作为基模型,提升50轮,最后得到训练准确率为100%,测试准确率为96%。相比于深度不受限的决策树分类器对相同数据进行训练和测试,准确率分别为100%和85%。准确率和损失随着迭代次数的变换关系如下图所示:
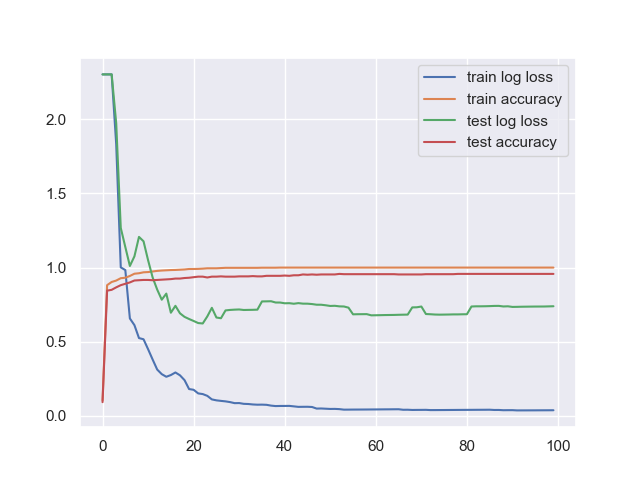
总结
本文介绍了如何将只可用于回归的GBDT扩展到二分类和多分类情形,并自实现算法和验证该算法的合理性。