本文主要介绍残差逼近——一种集成学习手段,以及如何从残差毕竟推导到梯度提升。
残差逼近
考虑一元回归问题,训练集大小为2,也就是$(\pmb x_1,y_1)$和$(\pmb x_2,y_2)$,设$y_1=1$,$y_2=10$。我们用一个弱学习器,学习并预测,得到$\hat{y}_1=\hat{y}_2=5$,显然弱学习器的学习结果与目标值间存在差距。这时考虑再用弱学习器学习数据的残差,也就是目标值与预测值的差:
\[\hat{\pmb \varepsilon}=\begin{bmatrix} y_1-\hat{y}_1&y_2-\hat{y}_2 \end{bmatrix}=\begin{bmatrix} -4&5 \end{bmatrix}\]假设弱学习器对残差的学习结果为$[-3\quad6]$,那么此时我们可以目标值的学习结果,和残差的学习结果相加,作为总的预测结果,也就是$[2\quad11]$,更接近目标值。这就是所谓的残差逼近,显然这样的步骤可以迭代多次,直到这些弱学习器的结果加起来足够逼近目标值。
程序实现
我们尝试用Python实现sklearn接口的上述算法
import numpy as np
from sklearn.svm import SVR
from sklearn.metrics import r2_score
class Boost:
def __init__(self, base_model=SVR, T=10) -> None:
'''
使用SVR模型作为弱回归器,迭代次数默认为10
'''
self.T = T
self.base_model = base_model
self.boost_model = [self.base_model() for i in range(self.T)]
def fit(self, X, y):
target = np.copy(y)
for i in range(self.T):
self.boost_model[i].fit(X, target)
target -= self.boost_model[i].predict(X)
return self
def predict(self, X):
return sum([model.predict(X) for model in self.boost_model])
def score(self, X, y):
return r2_score(y, self.predict(X))
以Boston和Diabetes数据集为例,我们来看残差逼近训练效果(数据已经过标准化):
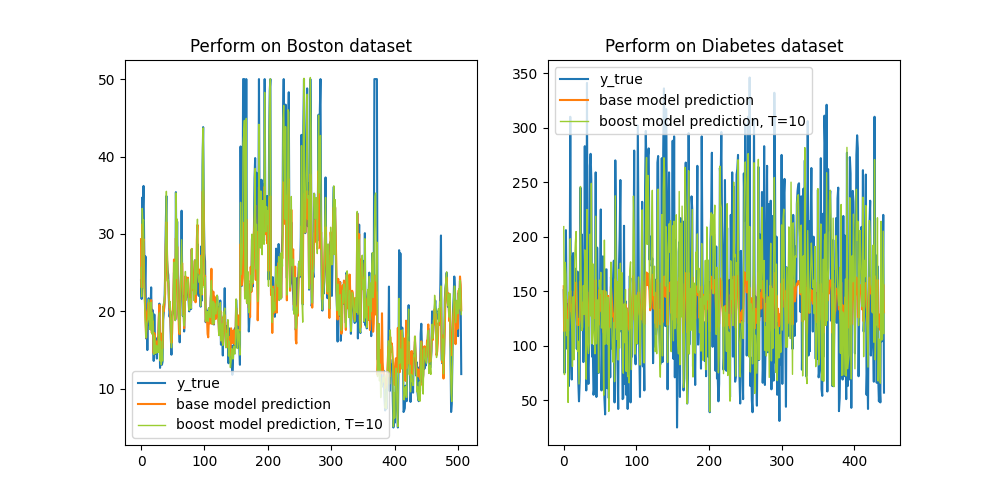
显然,经过10轮残差逼近后,模型的回归结果愈发毕竟目标值。现在考虑模型在数据集上的表现,分为训练误差与测试误差:
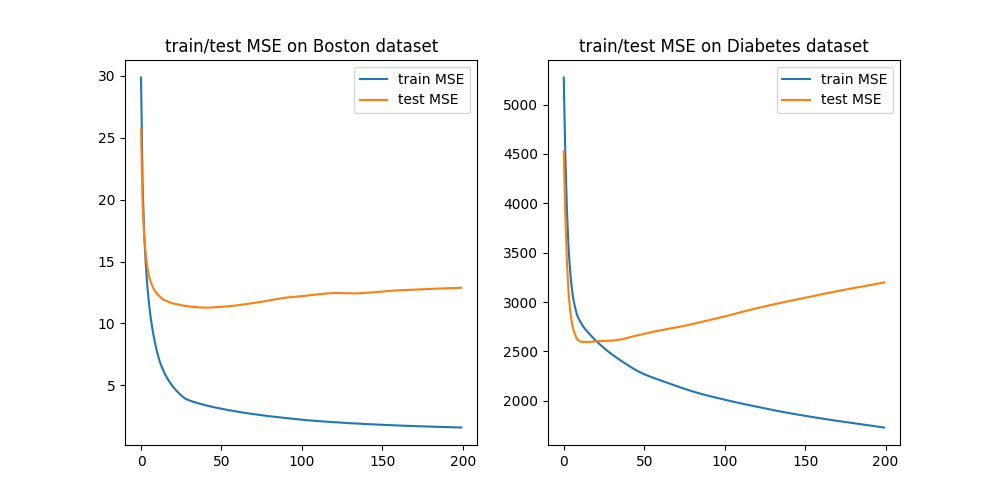
显然,由于我们一直追求对训练集残差的逼近,在训练集上出现了过拟合。但只要逼近轮数不要太多,效果总是比基础模型好得多。
梯度提升
显然残差逼近是一个加法模型,设第$n$轮训练出的基模型是$f_n$,那么总的预测模型就是
\[F_n=\sum_{i=1}^nf_n\tag1\]我们在第$n$轮的训练目标是学习残差:
\[\min_{f_n}\quad\frac12\sum_{i=1}^l\bigg((y_i-F_{n-1}(x_i)) -f_n(x_i)\bigg)^2\tag{2}\]实际上就是最小化均方误差,因为
\[F_{n-1}+f_n=F_n\]这样就从理论上解释了残差逼近的合理性。我们对(2)中的学习目标进行修改,等价于优化
\[\min_{\hat{\pmb y}}\quad l(\hat{\pmb y})=\frac12\sum_{i=1}^l\bigg((y_i-F_{n-1}(x_i))-\hat{y}_i\bigg)^2\tag{3}\]目标函数的梯度为
\[\nabla_{\hat{\pmb y}}l(\hat{\pmb y})=\hat{\pmb y}-(\pmb y-F_{n-1}(\pmb X))\]可以发现,均方误差对预测结果的负梯度,也就是当前需要学习的残差。因此,残差逼近等价于梯度下降,或者说,问题$(3)$其实近似于上一轮损失函数的一阶泰勒展开,我们这一轮想优化的就是这个展开式。因此,残差逼近方法也可以叫梯度提升。
我们发现,上面论述的成立依赖于平方损失函数的性质:平方损失函数求导后就是残差。因此,如果换作其他损失函数,比如绝对损失函数、$\varepsilon$-不敏感函数,拟合残差虽然有效,但缺少根据,比如下图是残差逼近算法在两数据集上的绝对损失。
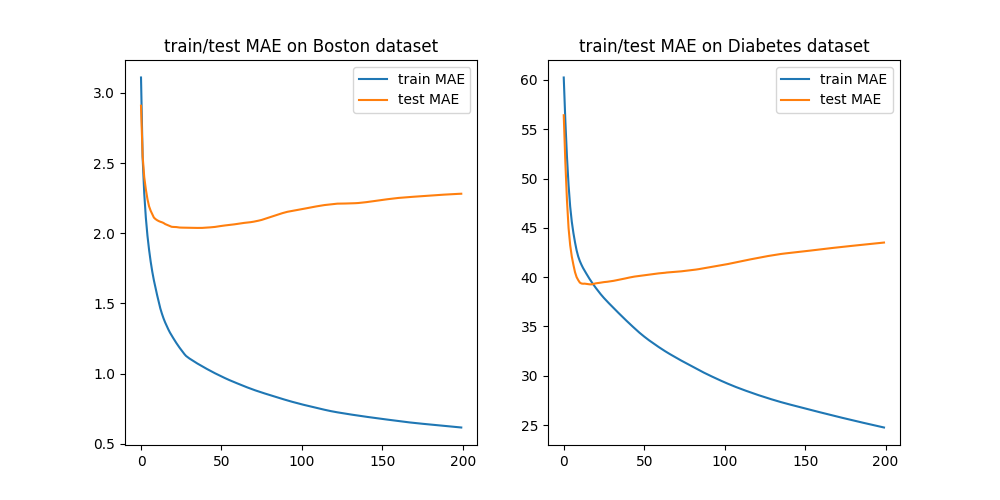
因此,广义的梯度梯度提升算法是不断拟合当前损失函数的负梯度。我们以绝对损失函数为例,则优化目标是
\[\min_{\hat{\pmb y}}\quad l(\hat{\pmb y})=\sum_{i=1}^l\bigg|(y_i-F_{n-1}(x_i))-\hat{y}_i\bigg|\tag{4}\]目标函数的梯度为(不严谨,零点处的梯度是一个区间,这里简化成0)
\[\nabla_{\hat{\pmb y}}l(\hat{\pmb y})=\text{sign}\bigg(\hat{\pmb y}-(\pmb y-F_{n-1}(\pmb X))\bigg)\]所以每轮拟合的是$-\nabla_{\hat{\pmb y}}l(\hat{\pmb y})$,显然这样拟合的速度会很慢,且效果不好。下图是300次迭代后模型在训练集和测试集上的表现:
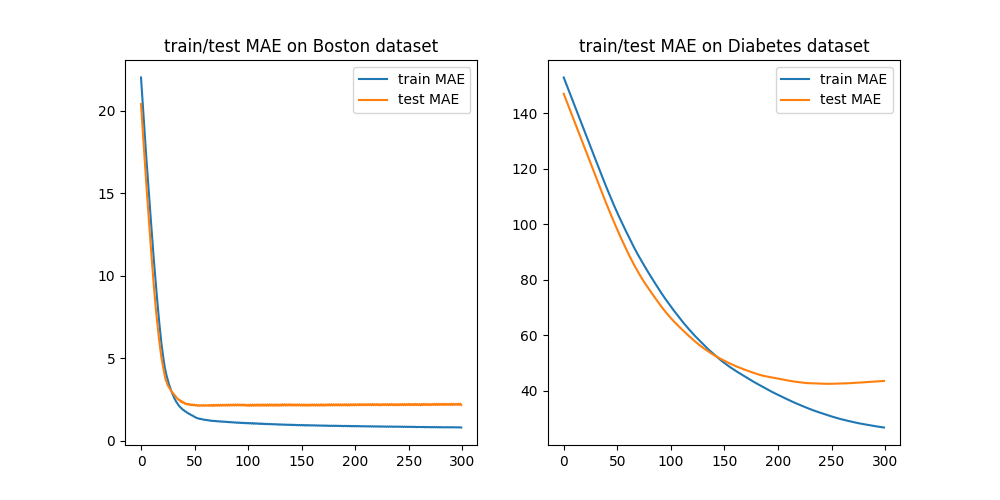
和前面相比,虽然训练误差效果不如一般的残差逼近,但在测试误差上取得了相似的效果,抑制了过拟合。
梯度提升树(GBDT)
我们上面的实验,都是用未经调参的SVR作为基模型。在现实应用中,通常是用决策树(回归树)作为梯度提升方法的基模型,此时的梯度提升方法就叫做梯度提升树(Gradient Boosting Decision Tree, GBDT)。我们尝试用回归树来进行绝对损失下的梯度提升:
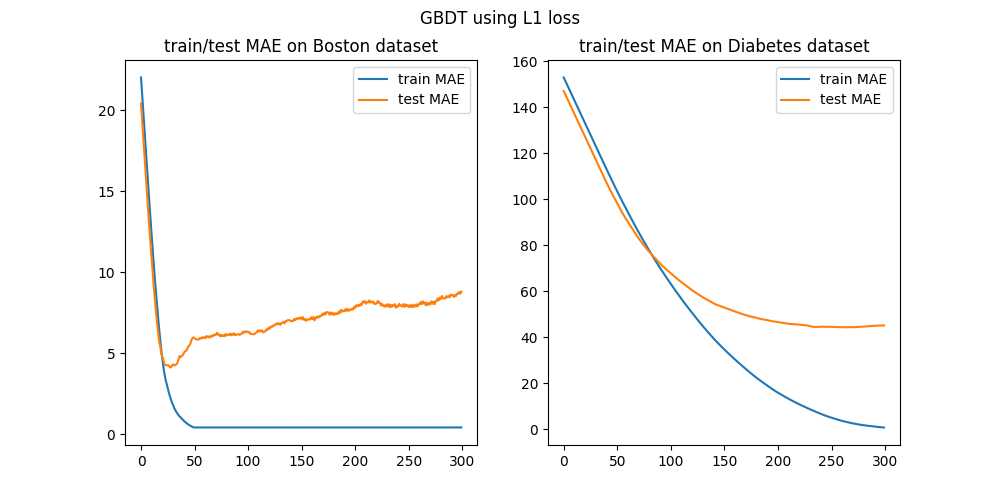
我们发现决策树作为基模型后,一是加速了训练误差的下降,二是加剧了过拟合。因此在Xgboost等算法软件包中,会对决策树进行复杂度的限制,也就是正则化技术。