近年来,深度学习领域关于图神经网络(Graph Neural Networks,GNN)的研究热情日益高涨,图神经网络已经成为各大深度学习顶会的研究热点。GNN处理非结构化数据时的出色能力使其在网络数据分析、推荐系统、物理建模、自然语言处理和图上的组合优化问题方面都取得了新的突破。
由于实习任务的缘故,笔者近期也在进行GNN的学习。作为一个方兴未艾的领域,目前有很多的博客文章对GNN领域进行介绍。在阅读一众文章后,我决定也下笔写一些关于GNN的文章,介绍GNN的原理和实现。笔者在今年实现了PyDyNet,仿PyTorch的深度学习框架并获得好评。因此我更“宏大”的目标是通过对GNN和当前的图神经网络框架的学习,基于PyDyNet去构建自己的图神经网络框架。
Data
在传统的深度学习领域,从最简单的表格数据,到更加复杂的视频数据和文本数据,它们都可以用一个张量去表示,数据越复杂,张量的维数越高。但图神经网络所处理的数据,即图数据,其具有拓扑结构的性质导致我们需要用多个张量来对其进行描述:
- 图的表示,通常是邻接矩阵;
- 节点的表示,即节点数$\times$节点特征维数;
- 边的表示,即边数$\times$边特征维数;
而实际上,除了图表示矩阵是必须的之外,后两者并不是必须的。
Mission
图的特殊结构带来的不仅是表示上的复杂度提升,也带来了任务的多样性。比如分类任务在图神经网络框架下就衍生出至少3个类型:
- 节点分类,比如判断分子式各节点是哪些元素;
- 图分类,比如判断哪种分子有毒;
- 边分类,比如判断信息传播链中,哪一条传播链异常。
要解决这些问题,主要的任务是考虑图的拓扑属性,从而更好表示节点、图和边。深度学习也是这个思路,即多层神经网络只是将数据的特征进行自动提取,然后基于这些新特征进行训练分类器。这是空间域图卷积中一个重要思路。以节点表示为例,节点的特征与相邻节点的特征相关,我们考虑用节点自身以及周围节点的特征的融合来表示该节点。这种熟悉的表示方式让人想到了卷积,这就是空域的图卷积,与之相对的还有谱域卷积。
GCN
如上所述,空域图卷积的思想很好理解,就是用节点的邻居节点特征来表示节点。而相对的,基于谱域的卷积涉及到谱图理论,一种离散数字信号处理的拓展理论,这里我们不做介绍,我们只需要知道:
- 当前的GCN主要是基于空间域的,因为它确实更容易直观理解,也比较契合机器学习和深度学习的特点;
- 基于谱域的GCN经过了几代的演化:
- 第一代GCN需要对每张图的图拉普拉斯矩阵进行特征分解,存在计算量大等缺陷;
- 第二代GCN也叫ChebNet,采用了切比雪夫多项式对卷积核近似,不再需要特征分解,提高了计算效率;
- 第三代GCN用一阶的切比雪夫多项式对ChebNet进行简化,从而引出了更简单的图卷积形式,该形式能够用空域卷积去解释。
- 基于谱域的图卷积有很可靠的理论基础,而空域卷积虽然直观,但缺乏厚实的理论支撑。目前有一个很经典的工作为GCN构建了一个理论框架:How Powerful are Graph Neural Networks?
本文将采用空域的视角来解释第三代GCN,也是最令人熟知的GCN。考虑下面的无向图,其中每个节点都有一个特征向量,我们分别用$\pmb x_i,(i=1,\cdots,5)$表示,记作
\[X^0=\begin{bmatrix} \pmb x_1&\pmb x_2&\pmb x_3&\pmb x_4&\pmb x_5 \end{bmatrix}^T\]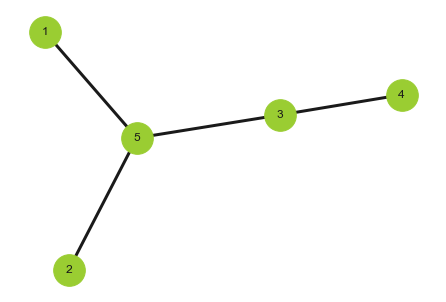
该图的拓扑结构可以用邻接矩阵表示:
\[A=\begin{bmatrix} 0&0&0&0&1\\ 0&0&0&0&1\\ 0&0&0&1&1\\ 0&0&1&0&0\\ 1&1&1&0&0\\ \end{bmatrix}\]现在考虑空域图卷积,我们用每个节点利用相邻节点的特征来构建新的特征(消息传递和聚合)。我们考虑最简单的加和,即该节点的新特征为邻居节点特征向量和。那么新一轮特征:
\[X^1=\begin{bmatrix} \pmb x_5\\ \pmb x_5\\ \pmb x_4+\pmb x_5\\ \pmb x_3\\ \pmb x_1+\pmb x_2+\pmb x_3 \end{bmatrix}=\begin{bmatrix} 0&0&0&0&1\\ 0&0&0&0&1\\ 0&0&0&1&1\\ 0&0&1&0&0\\ 1&1&1&0&0\\ \end{bmatrix}\begin{bmatrix} \pmb x_1\\\pmb x_2\\\pmb x_3\\\pmb x_4\\\pmb x_5 \end{bmatrix}=AX^0\]可以发现这样的以加和为聚合函数的消息传递过程,新特征等价于邻接矩阵乘以原特征。但上式中,我们少考虑了一项,即节点自身的特征也需要参与到新特征的构建上。此时我们只需要对上式稍作修改,将$A$改成$A+I$即可:
\[X^1=\tilde{A}X^0=(A+I)X^0\]而为了防止数值爆炸,保证稳定性,我们会将$\tilde{A}$进行归一化处理:
\[\hat{A}=D^{-\frac12}\tilde{A}D^{-\frac12}\]其中$D$是度矩阵,可以通过临邻接矩阵推出来:
\[d_{ij}=\begin{cases} \sum_{k=1}^n\tilde{A}_{ik}&i=j\\ 0&i\neq j \end{cases}\]因此,最终的消息传递以及聚合过程为
\[X^1=\hat{A}X^0\]接着按照一般神经网络的思路,我们加上可学习参数$W$,所以一个简单的GCN架构可以写成:
\[f_2(\hat{A}f_1(\hat{A}XW^0)W^1)\]其中$f_1$和$f_2$为任意激活函数。上式对应单隐层的GCN,此处省略了偏置项。
Think further
在上面的推导过程中,我们有2个人为设置:
- 图是无权图,每条边同等重要;
- 选用求和为聚合函数。
对于第一点,我们可能需要将邻接矩阵的元素扩展为正整数域,元素表示边权;对于第二点,实际上求和,求平均和求最大值是三种最常用的聚合函数,当然也存在其它的聚合函数,包括人为设计函数。聚合函数都需要满足可微以及排列不变性。可微很好理解,排列不变性即计算的过程中,元素的排列顺序不会对最终结果产生影响,比如求最大、求和、求平均都是排列不变性的。
事实上,消息传递聚合是一个抽象的过程,满足一种消息传递范式,在DGL和PyG等图神经网络框架中,消息传递范式成为了一个基类,框架衍生以及用户自定义的各种网络层,都需要继承这个基类。
消息传递范式:
\[\pmb x_i^{(k)}=\gamma^{(k)}\bigg(\pmb x_i^{(k+1)},\square_{j\in\mathcal{N}(i)}\phi^{(k)}\big(\pmb x_i^{(k-1)},\pmb x_j^{(k-1)},\pmb e_{j,i} \big) \bigg)\]其中$k$表示层数;$\pmb x_i^{(k)}$表示输入图的结点$i$在网络第$k$层时的特征向量;$\square$表示聚合函数,满足可微和排列不变性;$\mathcal{N}(i)$表示结点$i$的邻居结点;$\gamma$和$\phi$表示可微函数,可以是简单的激活函数,也可以是复杂的多层感知机;$\pmb e_{j,i}$表示节点$i$到$j$的有向边对应的特征向量,我们前面提到的边权就是最简单的边特征向量,维度为1。
以我们上一节引出的GCN为例,一个GCN层可以写作
\[\pmb x_i^{(k)}=\sum_{j\in\mathcal{N}(i)\cup\{i\}}\dfrac{1}{\sqrt{\deg(i)}\sqrt{\deg(j)}}(\pmb x_j^{(k-1)}W)\]如果加上偏置项则是
\[\pmb x_i^{(k)}=\sum_{j\in\mathcal{N}(i)\cup\{i\}}\dfrac{1}{\sqrt{\deg(i)}\sqrt{\deg(j)}}(\pmb x_j^{(k-1)}W)+\pmb b\]对应到上面的消息传递范式:
\[\begin{aligned} \gamma^{(k)}\bigg(\pmb x_i^{(k-1)}, \text{message}\bigg)&=(\dfrac{1}{\deg(i)}\pmb x_i^{(k-1)}+\text{message})W+\pmb b\\ \square&=\sum\\ \phi^{(k)}(\pmb x_i^{(k-1)},\pmb x_j^{(k-1)},\pmb e_{j,i})&=\dfrac{1}{\sqrt{\deg(i)}\sqrt{\deg(j)}}\pmb x_j^{(k-1)} \end{aligned}\]Summary
这里我们通过对基于谱域的GCN的介绍和推导,引出了基于空域的消息范式,它被当前很多的框架所广泛采用。