在机器学习中,存在这样一种情景,即数据集不是提前给定的,而是随着时间不断增加 (stream data)。以分类问题为例,该情景不断重复下面的循环:
- 学习器得到数据$\pmb x$;
- 学习器预测标签$\hat{y}$;
- 学习器得到$\pmb x$对应的真实标签$y$。
一个经典的例子是天气预报,$\pmb x$对应此时的观测,$\hat{y}$表示对天气的预报,而$y$是真实天气,只能第二天看到。这种学习过程称作在线学习 (on-line learning)。在当前大数据背景下,使用固定数据集训练的模型无法适应产品更新迭代的需要,每过一段时间就重新训练模型是很不理智的,这也是在线学习受到重视的原因。
设在线学习持续$T$轮,在第$t$轮,算法接收了一个样本$x_t\in\mathcal X$同时做出预测$\hat{y}_t\in\mathcal Y$;接着得到真实标签$y_t\in\mathcal Y$,显然就能得到损失$L(\hat{y}_t,y_t)$。在线学习的目标就是极小化$T$轮的累积损失:$\sum_{t=1}^TL(\hat{y}_t,y_t)$。
专家建议下的预测
在这一框架下,学习器在得到$x_t$的同时,还会得到$N$位专家的建议$\hat{y}_{t,i}\in\mathcal{Y}$,我们应当从这些建议中,选择一个作为预测标签$\hat{y}_t$。事实上可以将“专家”理解为假设空间的假设$h$,针对输入的instance输出label。我们每轮可以选择不同专家的建议,得到累积损失。显然,存在一位专家,他提出的建议在$T$轮中的累积损失是最小的,相当于在离线情况下,模型能够得到的最好表现。显然在线学习下,我们的累积损失不会小于该专家预测下的累积损失。我们将两种在线学习的累积损失和离线情况下最小的累积损失间的差距称作“遗憾” (regret):
\[R_T=\sum_{i=1}^TL(\hat{y}_t,y_t)-\min_{i=1}^N\sum_{t=1}^NL(\hat{y}_{t,i},y_t).\tag{1}\]考虑0-1损失的分类情形,在可实现情况 (realizable case)下,也就是存在一个专家,他可以正确分类每一轮的输入特征,我们讨论错误界模型(Mistake bound model),它研究的是“在学到一个特定概念前,我们需要多少次判断错误”。由于是可实现情况,存在一个$T$,在$T$轮后,我们学到了一个不犯错的概念,因此在后续的在线学习中,我们不再犯错,因此存在一个犯错误的最大次数。
对于任意概念$c$,我们定义学习算法$\mathcal{A}$找到这个概念所需要犯的最大错误次数
\[M_{\mathcal A}(c)=\max_{x_1,\cdots,x_T}|\text{mistakes}(\mathcal{A}, c)|.\tag2\]类似的,在概念类$\mathcal C$中,我们定义最大犯错次数
\[M_{\mathcal A}(\mathcal C)=\max_{c\in\mathcal C}M_{\mathcal A}(c).\tag3\]给定概念类和学习算法,我们希望求出$M_{\mathcal A}(\mathcal{C})$的上界$M$。
Halving算法
下面介绍Halving算法,一个朴素的在线学习算法,有比较好的犯错次数上界。

Halving算法在一开始会接受所有专家的投票,在循环过程中,如果存在专家预测错误,则不再接受该专家的建议,因为它必然不是我们想要的0错误概念。显然这样的操作会帮我们找到这样的概念。在假设空间$\mathcal H$有限的情况下,我们有
\[M_{\text{Halving}}(\mathcal H)\leq\log_2|\mathcal{H}|.\tag{4}\]令$opt(\mathcal H)$为假设空间$\mathcal H$下的最优错误界,我们有
\[\text{VCdim}(\mathcal H)\leq opt(\mathcal H)\leq M_{\text{Halving}}(\mathcal H)\leq\log_2|\mathcal{H}|.\tag{5}\]Weighted majority算法(WM)
可以发现Halving算法是很冒进的算法,这是由于我们知道这是一个realizable case。而当我们的目标概念不在假设空间中,即non-realizable case,我们的策略要更严谨一些,也就是Weight majority算法:我们会接受出错专家的建议,但它的重要性 (权重)会下降:
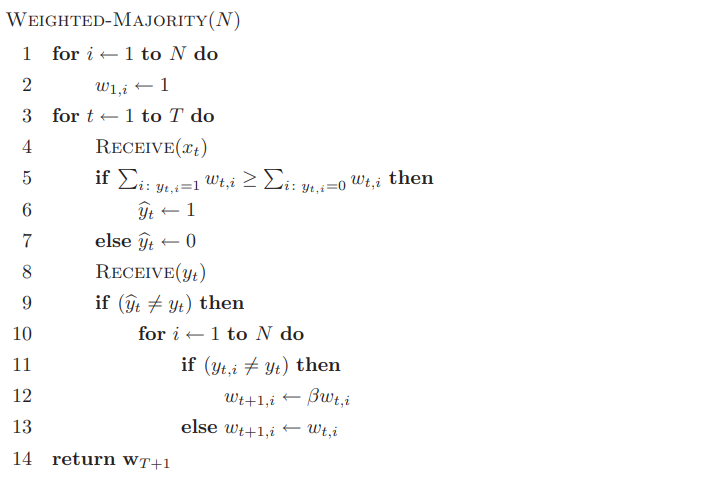
可以发现WM算法只适用于二分类。我们设$\beta\in[0,1)$,当$\beta=0$,WM算法退化成Halving算法。在不可实现情形下,(4)和(5)的界不再适用,即犯错次数不再有界。下面的定理揭示了WM算法的犯错次数关于$T$的变化趋势。
令$m_T$为$T$轮之后WM算法犯错次数,$m^*_T$是最好的专家在这$T$轮中犯错次数,$\beta\in(0,1)$,我们有
\[m_T\leq\dfrac{\log N+m^*_T\log\frac1\beta}{\log\frac2{1+\beta}}\tag6\]Randomized WM算法(RWM)
在0-1损失的确定性算法下,我们无法实现$o(T)$的遗憾界,也就是遗憾界的最坏情况是与$T$成正比的。我们可以构造这个最坏情况,我们根据算法的输出$\hat{y}_t$给出$y_t$:$\hat{y}_t=1$,我们就令$y_t=0$,反之亦然。那么此时$m_T=T$。考虑$N=2$,即两个专家的决策,一个专家一直建议$\hat{y}_t=1$,另一个建议恰好相反。那么$m^*_T\leq\frac T2$,因此遗憾界
\[R_T=m_T-m^*_T\geq\frac T2\]也就是无法实现$o(T)$。消除这一坏结果有两种方法:
- 改用凸损失函数;
- 改用随机算法.
Randomized WM算法将随机性加入了WM算法,用一个概率分布$\pmb p_t$来预测$\hat{y}_t$:
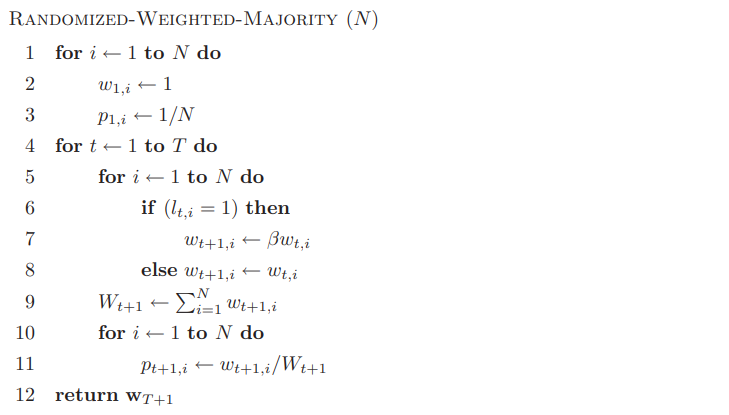
在第$t$轮中,我们会得到一个损失向量$\pmb l_t$,其第$i$分量是做出采取第$i$个专家建议的损失,所以此轮的期望损失为$L_t=\sum_{i=1}^Np_{t,i}l_{t,i}$,累积期望损失就是$\mathcal L_t=\sum_{t=1}^TL_{t}$。定义专家建议的最小损失为
\[\mathcal{L}_T^\min=\min_{i\in\{1,\cdots,N\}}\mathcal{L}_{T,i}=\min_{i\in\{1,\cdots,N\}}\sum_{t=1}^Tl_{t,i}\tag7\]此时的遗憾界就是
\[R_T=\mathcal{L}_T-\mathcal L_T^\min\]可以证明,RWM算法实现了$O(\sqrt{T\log N})$,实际上是$2\sqrt{T\log N}$的遗憾界。
Exponential weighted average算法
前面提到,降低遗憾界的方法除了采用随机算法,还可以采用凸的,值域为$[0,1]$的损失函数。Exponential weighted average算法正是采取了这样想法,而且它是确定性的:
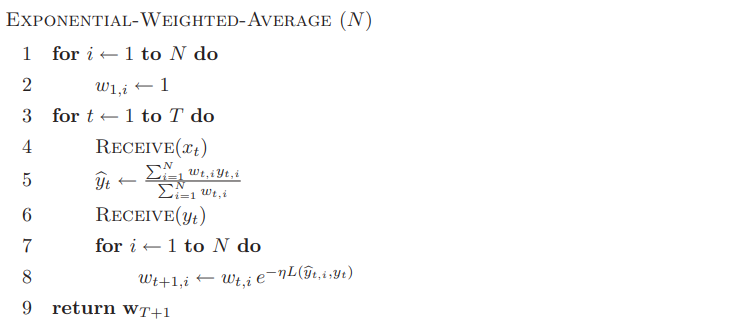
该算法可得到更近的遗憾界
\[R_T\leq\sqrt{\frac T2\log N}\]复杂度上同样是$O(\sqrt{T\log N})$的。
总结
我们介绍了在线学习和遗憾界的基本概念,同时考察了遗憾界的复杂度,以及如何通过修改算法得到它的最优复杂度。