LIBLINEAR是一个用于大规模线性分类的开源库,它支持逻辑回归和线性支持向量机。与LIBSVM相比,LIBLINEAR支持更多的模型,更大的数据和更快的训练速度,但它取消了LIBSVM中对核函数的支持,从而达到提升运行速度的目的。
LIBLINEAR支持的模型
LIBLINEAR目前有12种模型,分别是Crammer-Singer多分类模型、单类SVM对偶模型,以及下表的10种模型:
| L1正则原问题 | L2正则原问题 | L2正则对偶问题 | |
|---|---|---|---|
| L1-loss SVC | √ | ||
| l2-loss-SVC | √ | √ | √ |
| Linear Regression | √ | √ | √ |
| L1-loss SVR | √ | ||
| l2-loss SVR | √ | √ |
其中L1-loss就是Hinge loss:
\[l_1(\pmb w;\pmb x,y)=\max(0, 1-y\pmb w^T\pmb x)\]对应的,L2-loss是Hinge loss的平方:
\[l_2(\pmb w;\pmb x,y)=\max(0, 1-y\pmb w^T\pmb x)^2\]我们阅读了相关文献,对这些模型方法进行解读。
Crammer-Singer多分类
在https://welts.xyz/2022/02/03/crammer_singer/中,我们对LIBLINEAR中的Crammer-Singer算法进行解读,它使用坐标下降进行求解下面的子问题
\[\begin{aligned} \min_{\pmb\alpha}\quad&f(\pmb\alpha)=\frac12\sum_{m=1}^k\Vert\pmb w_{m}\Vert^2+\sum_{i=1}^l\sum_{m=1}^ke_i^m\alpha_i^m\\ \text{s.t.}\quad&\sum_{m=1}^k\alpha_i^m=0,i=1,\cdots,l\\ &\alpha_i^m\leq C_{y_i}^m,i=1,\cdots,l,m=1,\cdots,k \end{aligned}\]其中
\[\begin{aligned} \pmb w_m&=\sum_{i=1}^l\alpha_i^m\pmb x_i,\forall m,\\ \pmb\alpha&=[\alpha_1^1,\cdots,\alpha_1^k,\cdots,\alpha_l^1,\cdots,\alpha_l^k]^T\\ C_{y_i}^m&=\begin{cases} 0&\text{if }y_i\neq m,\\ C&\text{if }y_i=m. \end{cases} \end{aligned}\]单分类SVM
单类SVM所求解的是下面的对偶问题
\[\begin{aligned} \min_{\pmb\alpha}\quad&\frac12\pmb\alpha^TQ\pmb\alpha\\ \text{s.t.}\quad&0\leq\alpha_i\leq\frac1{\nu l},i=1,\dots,l\\ &\pmb e^T\pmb\alpha=1 \end{aligned}\]其中$Q_{ij}=\pmb x_i^T\pmb x_j$。LIBLINEAR采用两层的坐标下降框架求解该对偶问题,我们在https://welts.xyz/2022/01/31/one_class/中进行了详解,这里也用到了LIBSVM中的一些方法。
L1正则化模型
LIBLINEAR支持L1正则化的L2-loss SVM分类和对率回归(逻辑回归),且都是用坐标下降法求解原问题:
\[\min_{\pmb w}\quad f(\pmb w)=\Vert\pmb w\Vert_1+C\sum_{i=1}^l\xi(\pmb w;\pmb x_i,y_i)\]其中$\xi$是损失函数,随着模型的不同而发生变化。由于两者的损失函数的性质不同(即可导性不同),即使采用同样的优化方法,细节上也有不少不同。我们在https://welts.xyz/2022/01/30/l1/中对两种方法进行解读。由于我们这里是对提出该方法的论文《A Comparison of Optimization Methods and Software for Large-scale L1-regularized Linear Classification》进行分析,所以其中也有其他的求解方法,如果你有兴趣可以深入了解。
对率回归的对偶问题
《Dual coordinate descent methods for logistic regression》提出了用坐标下降法求解对率回归问题的方法,即求解
\[\begin{aligned} \min_{\pmb\alpha}&\quad \frac12\pmb\alpha^TQ\pmb\alpha+\sum_{i:\alpha_i>0}\alpha_i\log\alpha_i+\sum_{i:\alpha_i<C}(C-\alpha_i)\log(C-\alpha_i)\\ \text{s.t.}&\quad0\leq\alpha_i\leq C,i=1,\cdots,l \end{aligned}\]这里设计的坐标下降法不仅能够解决对率回归数值计算上的问题(因为有对数运算),同时在性能上超过了当时大部分训练对率回归分类器的算法。我们在https://welts.xyz/2022/01/26/dcd_lr/中对该算法进行了详细的解读。
对率回归的原问题
在《Trust Region Newton Method for Large-Scale Logistic Regression》中,作者提出了训练大型逻辑回归问题的新算法,置信域牛顿法。并通过实验证明了该算法效率比常用的拟牛顿法更高,同时也将该算法应用到L2-SVM的求解上。
算法求解的是
\[\min_{\pmb w}\quad f(\pmb w)=\frac12\pmb w^T\pmb w+C\sum_{i=1}^l\log(1+\exp(-y_i\pmb w^T\pmb x_i))\]在https://welts.xyz/2021/12/19/tron/中,我们对该算法进行解读。
支持向量回归的对偶问题求解
经典的SVM是用于二分类问题,在LIBLINEAR中,我们用坐标下降法求解其对偶问题,也就是
\[\begin{aligned} \min_{\pmb\alpha}&\quad f(\pmb\alpha)=\frac12\pmb\alpha^T\bar{Q}\pmb\alpha-\pmb{e}^T\pmb{\alpha}\\ \text{s.t.}&\quad0\leq\alpha_i\leq U,i=1,\cdots,l \end{aligned}\]其中$\bar{Q}=Q+D$,$D$是对角矩阵。对于不同的SVM,$D$和$U$的定义不同:
| 问题类型 | $D_{ii}$ | $U$ |
|---|---|---|
| L1-SVM | 0 | $C$ |
| L2-SVM | $1/2C$ | $\infty$ |
坐标下降法在这里能够得到解析解,因此比较简单,详情可参考https://welts.xyz/2021/12/02/dcdm/.
支持向量回归的原问题求解
LIBLINEAR中采用坐标下降方法求解SVM分类原问题。为了确保收敛性,LIBLINEAR采用线搜索的方法确定牛顿步径,这是一个创新点,详情参考https://welts.xyz/2022/01/18/cdm/.
支持向量回归的求解
支持向量回归原问题:
\[\min\quad f(\pmb w)=\frac12\pmb w^T\pmb w+C\sum_{j=1}^l\xi_{\varepsilon}(\pmb w;\pmb x_j,y_j)\]其中$C$是正实数,而$ξ_\varepsilon$是损失函数,可以$\varepsilon$-不敏感损失函数,或者是它的平方:
\[\xi_{\varepsilon}(\pmb w;\pmb x_j,y_j)=\begin{cases} \max(\vert\pmb w^T\pmb x_j-y_j\vert-\varepsilon,0)&\text{or}\\ \max(\vert\pmb w^T\pmb x_j-y_j\vert-\varepsilon,0)^2 \end{cases}\]如图所示
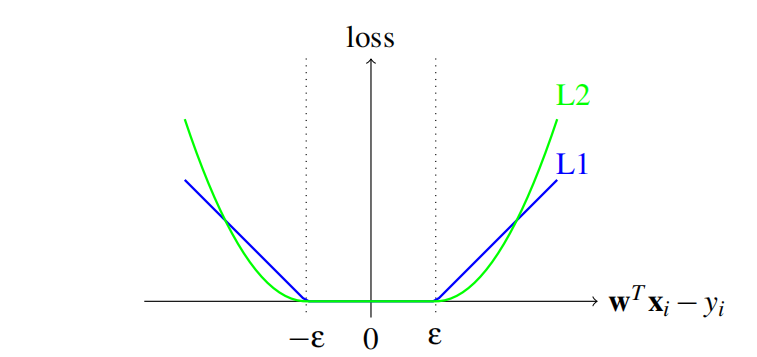
LIBLINEAR采用带置信域的牛顿法来求解L2-loss SVR原问题。上述问题的对偶问题为
\[\begin{aligned} \min_{\pmb\alpha^+,\pmb\alpha^-}\quad&f_A(\pmb\alpha^+,\pmb\alpha^-)=\frac12(\pmb\alpha^+-\pmb\alpha^-)^TQ(\pmb\alpha^+-\pmb\alpha^-)+\\&\quad\sum_{i=1}^l\bigg(\varepsilon(\alpha_i^++\alpha^-)-y_i(\alpha_i^+-\alpha_i^-)+\frac\lambda2((\alpha^{+}_i)^2+(\alpha^-_i)^2)\bigg)\\ \text{s.t.}\quad&0\leq\alpha_i^+,\alpha_i^-\leq U,i=1,\cdots,l \end{aligned}\]其中$Q_{ij}=\pmb x_i^T\pmb x_j$。这里$λ$和$U$也会随着问题类型而不同
| 问题类型 | $\lambda$ | $U$ |
|---|---|---|
| L1-loss SVR | 0 | $C$ |
| L2-loss SVR | $1/2C$ | $\infty$ |
LIBLINEAR采用改进的坐标下降法求解两种对偶问题。我们这里一共提到了三种支持向量回归模型问题,都在https://welts.xyz/2022/01/21/svr/中进行了解析。
我们将上面的解析综合起来,编写成PDF,你可以通过
git clone https://github.com/Kaslanarian/liblinear-sc-reading
获取。