原文:https://www.csie.ntu.edu.tw/~cjlin/papers/cddual.pdf.
参考:林智仁教授的talk,https://www.csie.ntu.edu.tw/~cjlin/talks/msri.pdf.
引入
对于$C$-SVC模型,其原问题:
\[\begin{aligned} \min_{\pmb w,b\pmb\xi}&\quad\frac12\pmb w^T\pmb w+C\sum_{i=1}^l\xi_i\\ \text{s.t.}&\quad y_i(\pmb w^T\pmb x_i+b)\geq1-\xi_i\\ &\quad\xi_i>0,i=1,\cdots,l \end{aligned}\]其对偶问题为
\[\begin{aligned} \min_{\pmb\alpha}&\quad\frac12\pmb\alpha^TQ\pmb\alpha-\pmb e^T\pmb\alpha\\ \text{s.t.}&\quad\pmb{y}^T\pmb\alpha=0\\ &\quad0\leq\alpha_i\leq C,i=1,\cdots,l \end{aligned}\]其中$Q_{ij}=y_iy_j\pmb{x}_i^T\pmb x_j$. 我们常常会解对偶问题来获得SVM问题的解。在对偶问题的限制条件中有一个等式约束:
\[\pmb y^T\pmb\alpha=\sum_{i=1}^ly_i\alpha_i=0\]这一约束来源于拉格朗日函数
\[\mathcal{L}(\pmb w,b,\pmb\alpha)=\frac12\pmb w^T\pmb w+\sum_{i=1}^l\alpha_i(1-y_i(\pmb w^T\pmb x_i+b))\]要求其对$b$的偏导数为0。它导致我们无法通过基础的坐标下降去求解,所以至少让两个变量可以活动,其他变量被固定。SMO算法采用的正是这样的方法:
- 选取一对需更新的变量$\alpha_i$和$\alpha_j$;
- 固定除了$\alpha_i$和$\alpha_j$以外的参数,对活动参数进行更新。
SMO的详细步骤可参考:
- 大致流程:https://welts.xyz/2021/07/09/smo/;
- 如何选择变量:https://welts.xyz/2021/07/10/wss/;
- 如何更新活动参数:https://welts.xyz/2021/07/11/libsmo/;
- SMO算法的Python实现:https://welts.xyz/2021/09/25/mysvm/.
而在《A Dual Coordinate Descent Method for Large-scale Linear SVM》中,作者提出了一次只更新一个变量的方式求出该对偶问题的解。
问题拓展与重构
事实上,我们在上面提到的$C$-SVC只是多种SVM中的一种,它采用的是Hinge loss。我们还可以将Hinge loss的平方作为损失函数:
\[f_1(x)=\max(0, 1-x)\\ f_2(x)=\max(0, 1-x)^2\\\]采用前一种损失函数的SVM称作L1-SVM,后一种称作L2-SVM。
在前面,模型的判别函数形式为
\[f(\pmb x)=\pmb w^T\pmb x+b\]而通过对数据进行增广:
\[\pmb x_i^T\gets[\pmb x_i^T,1]\quad\pmb w^T\gets[\pmb w^T,b].\]我们可以简化判别函数:
\[f(\pmb x)=\pmb w^T\pmb x\]这里偏置项$b$被消去,导致在拉格朗日函数中,我们不再需要对$b$求偏导,也就是等式约束
\[\pmb y^T\pmb\alpha=0\]被消去。由此SVM的对偶问题被重构:
\[\begin{aligned} \min_{\pmb\alpha}&\quad f(\pmb\alpha)=\frac12\pmb\alpha^T\bar{Q}\pmb\alpha-\pmb{e}^T\pmb{\alpha}\\ \text{s.t.}&\quad0\leq\alpha_i\leq U,i=1,\cdots,l \end{aligned}\]其中$\bar{Q}=Q+D$,$D$是一个对角矩阵。对于不同的SVM,$D$和$U$的定义不同:
| SVM类型 | $D_{ii}$ | $U$ |
|---|---|---|
| L1-SVM | $0$ | $C$ |
| L2-SVM | $1/2C$ | $\infty$ |
对偶坐标下降法(DCDM)
正如算法(Dual Coordinate Descent Method, DCDM)的名称,其想法十分朴素:每次更新一个变量,也就是
while alpha not optimal:
for i in range(1, l):
min f(..., alpha_i, ...)
给定当前的待优化变量$\pmb\alpha$,令
\[\pmb{e}_i=[0,\cdots,0,1,0,\cdots,0]^T\]也就是第$i$位为1,其它位置为0的向量。我们优化$\alpha_i$,其实是解下面的问题:
\[\min_{d}\quad f(\pmb\alpha+d\pmb e_i)=\frac12Q_{ii}d^2+\nabla_i f(\pmb\alpha)d+\text{constant}\]在没有限制的情况下,很容易求出最优的$d$
\[d^*=-\dfrac{\nabla_if(\pmb\alpha)}{Q_{ii}}\]但考虑更新前后都要有$\alpha_i\in[0,U]$,因此
\[\alpha_i\gets\min(\max(\alpha_i-\dfrac{\nabla_if(\pmb\alpha)}{Q_{ii}},0), U)\]对于L1-SVM,$U$就是参数$C$;对于L2-SVM,由于没有上界,所以可以简化成:
\[\alpha_i\gets\max(\alpha_i-\dfrac{\nabla_if(\pmb\alpha)}{Q_{ii}},0)\]算法在每次求$d^*$时都要求梯度,也就是
\[\begin{aligned} \nabla_if(\pmb\alpha)&=(Q\pmb\alpha)_i-1\\ &=\sum_{j=1}^lQ_{ij}\alpha_j-1\\ &=\sum_{j=1}^ly_iy_j\pmb x_i^T\pmb x_j\alpha_j-1 \end{aligned}\]因为该算法考虑的是大规模数据下的SVM,也就是数据量$l$和特征数$n$很大的情况,因此存储极大的$Q_{l\times l}$是不合理的,这导致$Q_{ij}$无法直接存取,每次只能通过计算得到。观察上式,我们发现求$\nabla_if(\pmb{\alpha})$的开销是$O(ln)$。为了减少开销,算法选择保存模型判别函数的参数$\pmb w$:
\[\pmb w=\sum_{j=1}^ly_j\alpha_j\pmb x_j\]这样每次求梯度就可以减小计算量(削减到$O(n)$):
\[\nabla_if(\pmb\alpha)=y_i\pmb w^T\pmb x_i-1\]因为$\pmb w$是关于$\pmb\alpha$的变量,因此需要我们动态维护。我们设$\bar\alpha_i$为更新前的$\alpha_i$,在对$\alpha_i$进行优化后,对$\pmb w$的更新:
\[\pmb w\gets\pmb w+(\alpha_i-\bar{\alpha}_i)y_i\pmb x_i\]显然这里的开销也是$O(n)$。
我们在这里写出L1-SVM上的对偶坐标下降法算法:
\[\begin{aligned} &\text{while }\pmb{\alpha}\text{ is not optimal}\\ &\quad\text{for }i=1,\cdots,l\\ &\quad\quad\bar{\alpha}_i\gets\alpha_i\\ &\quad\quad G=y_i\pmb{w}^T\pmb{x}_i-1\\ &\quad\quad\text{if }\alpha_i\text{ can be changed}\\ &\quad\quad\quad\alpha_i\gets\min(\max(\alpha_i-\frac{G}{Q_{ii}},0) ,C)\\ &\quad\quad\quad\pmb{w}\gets\pmb{w}+(\alpha_i-\bar{\alpha}_i)y_i\pmb{x}_i \end{aligned}\]这里的“$\alpha_i$ can be changed”就是解出来的$d^*$不为0,否则$\pmb\alpha$在原地踏步。事实上这里存在三种原地踏步的情况:
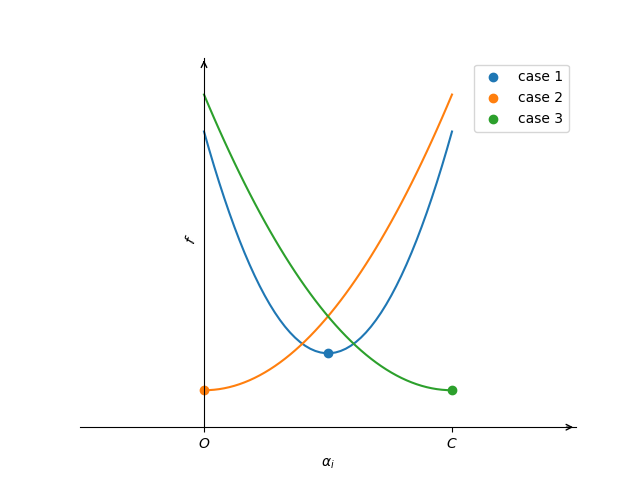
- 此时$\alpha_i$已经是最优的了,即$\nabla_i f(\pmb\alpha)=0$;
- $\alpha_i=0$,函数在$[0,C]$上递增,即$\nabla_if(\pmb\alpha)\geq0$;
- $\alpha_i=C$,函数在$[0,C]$上递减,即$\nabla_if(\pmb\alpha)\leq0$.
这些情况下,解出来的$d^*$都是0,我们可以提前判断而避免无意义的更新。文章引入“投影梯度”概念:
\[\nabla_i^Pf(\pmb\alpha)=\begin{cases} \nabla_if(\pmb\alpha)&\text{if }0<\alpha_i<U,\\ \min(0,\nabla_if(\pmb\alpha))&\text{if }\alpha_i=0,\\ \max(0,\nabla_if(\pmb\alpha))&\text{if }\alpha_i=U,\\ \end{cases}\]当投影梯度$\nabla^P_if(\pmb\alpha)=0$,$\alpha_i$已经是最优点了。事实上,我们上面的图像和分析涵盖了这里投影梯度为0的所有情况。
核方法下的DCDM
我们前面的分析基于的都是线性SVM,若使用了核方法,梯度就无法像线性SVM下通过维护$\pmb w$来实现,因为此时
\[\pmb w=\sum_{j=1}^l\alpha_iy_i\phi(\pmb x_i)\]但$\phi(\pmb x_i)$是维度极高且常常是不可知的。看起来我们只能退而求其次,采用原始的$O(ln)$方法计算梯度;但实际上,我们可以直接维护梯度向量$\nabla f(\pmb\alpha)$,每次更新一个$\alpha_i$后,便对梯度向量进行更新:
\[\nabla f(\pmb\alpha)\gets\nabla f(\pmb\alpha)+\bar{Q}_{:,i}(\alpha_i-\bar{\alpha}_i)\]算法实现的技巧
文章提到了两种提高算法效率的方法:
- 随机排列(Random permutation);
- 收缩(Shrinking).
随机排列的思想类似于SGD,SGD会随机打乱样本,再计算部分数据的梯度作为真实梯度的无偏估计,然后进行梯度下降,以降低数据的顺序对学习效果的影响。DCDM的随机排列在每个大循环中,先打乱数据的顺序(即生成排列$\pi$),再依次更新$\alpha^{\pi(i)}$,可以加快收敛的速度。
收缩是一种启发式算法,在LIBSVM中也有体现,可参考https://welts.xyz/2021/07/12/shrink/。这里的收缩针对的是一些值为$0$或$U$的$\alpha_i$,算法认为它们大概率不会在最近几个优化循环发生改变,因此不去思考它们,从而缩小问题的规模。
总结
在LIBSVM和一些旧的SVM软件包中,常常用SMO算法求解,但在《A Dual Coordinate Descent Method for Large-scale Linear SVM》中,作者提出了使用了更为高效的单变量坐标下降去求解SVM问题,这一算法被部署到了LIBLINEAR中,一定程度上帮助其成为大数据下高效训练线性SVM的软件包。