原文地址: https://www.jmlr.org/papers/volume13/ho12a/ho12a.pdf.
建议先阅读:
- 对偶坐标下降法: https://welts.xyz/2021/12/02/dcdm/;
- 置信域牛顿法: https://welts.xyz/2021/12/19/tron/;
- 支持向量回归的问题转化: https://welts.xyz/2021/09/16/svr/.
LIBLINEAR中的回归问题
给定数据集${\pmb x_j,y_j}_{j=1}^l,\pmb x_j\in\mathbb{R}^n,y_j\in\mathbb{R}$,支持向量回归(Support Vector Regression, SVR)求解的是下面的优化问题:
\[\min\quad f(\pmb w)=\frac12\pmb w^T\pmb w+C\sum_{j=1}^l\xi_{\varepsilon}(\pmb w;\pmb x_j,y_j)\]其中$C$是正实数,而$\xi_\varepsilon$是损失函数,可以$\varepsilon$-不敏感损失函数,或者是它的平方:
\[\xi_{\varepsilon}(\pmb w;\pmb x_j,y_j)=\begin{cases} \max(\vert\pmb w^T\pmb x_j-y_j\vert-\varepsilon,0)&\text{or}\\ \max(\vert\pmb w^T\pmb x_j-y_j\vert-\varepsilon,0)^2 \end{cases}\]两种损失函数示意图:
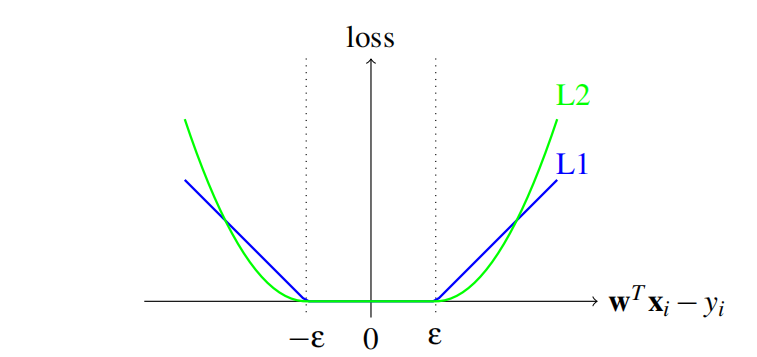
采用$\varepsilon$-不敏感损失函数的SVR称作L1-loss SVR,采用其平方的SVR为L2-loss SVR。
类似我们在前面解读过的对偶坐标下降法求解L1-SVM和L2-SVM对偶问题,SVR的对偶问题:
\[\begin{aligned} \min_{\pmb\alpha^+,\pmb\alpha^-}\quad&f_A(\pmb\alpha^+,\pmb\alpha^-)=\frac12(\pmb\alpha^+-\pmb\alpha^-)^TQ(\pmb\alpha^+-\pmb\alpha^-)+\\&\quad\sum_{i=1}^l\bigg(\varepsilon(\alpha_i^++\alpha^-)-y_i(\alpha_i^+-\alpha_i^-)+\frac\lambda2((\alpha^{+}_i)^2+(\alpha^-_i)^2)\bigg)\\ \text{s.t.}\quad&0\leq\alpha_i^+,\alpha_i^-\leq U,i=1,\cdots,l \end{aligned}\]其中$Q_{ij}=\pmb x_i^T\pmb x_j$,而类似分类问题,这里$\lambda$和$U$也会随着问题类型而不同:
| 问题类型 | $\lambda$ | $U$ |
|---|---|---|
| L1-loss SVR | 0 | $C$ |
| L2-loss SVR | $1/2C$ | $\infty$ |
因此,可以将上面的双变量问题重整为单变量问题:
\[\pmb\alpha=\begin{bmatrix} \pmb\alpha^+\\ \pmb\alpha^- \end{bmatrix},f_A(\pmb\alpha)=\frac12\pmb\alpha^T\begin{bmatrix} \bar{Q}&-Q\\ -Q&\bar{Q}\\ \end{bmatrix}\pmb\alpha+\begin{bmatrix} \varepsilon\pmb e-\pmb y\\ \varepsilon\pmb e+\pmb y\\ \end{bmatrix}^T\pmb\alpha\]其中$\bar{Q}=Q+\lambda I$,$\lambda$的定义如上表所示;$\pmb e$是一个全一向量。对偶问题的解和原问题的解满足下面的关系:
\[\pmb w^*=\sum_{i=1}^l\big(\alpha_i^{+*}-\alpha_i^{-*}\big)\pmb x_i\]值得注意的是对偶问题最优性条件:
\[(\alpha_i^+)^*(\alpha_i^-)^*=0,i=1,\cdots,l\]该对偶问题的规模是$2l$,而分类问题(SVC)的规模是$l$,我们当然可以继续使用求解SVC对偶的方法求解SVR对偶问题,但这样会造成计算代价的高昂。因此《Large-scale Linear Support Vector Regression》这篇文章便讨论如何改进原来的算法,使其适用于SVR问题。
置信域牛顿法求解
考虑带置信域的牛顿法求解L2 -loss SVR:

论文中的(7)式是循环终止条件,也就是梯度足够小;(6)式是置信域牛顿法的模型子问题。
在每一轮迭代中,都需要计算当前的截断牛顿步径,那么就必然需要计算目标函数梯度和黑塞矩阵。L2-loss SVR的梯度:
\[\nabla f(\pmb w)=\pmb w+2C(X_{I_1,:})^T(X_{I_1,:}\pmb w-\pmb y_{I_1}-\varepsilon\pmb e_{I_1})-2C(X_{I_2,:})^T(-X_{I_2}\pmb w+\pmb y_{I_2}-\varepsilon\pmb e_{I_2})\]其中
\[X=[\pmb x_1,\cdots,\pmb x_l]^T,I_1=\{i\vert\pmb w^T\pmb x_i-y_i>\varepsilon\},I_1=\{i\vert\pmb w^T\pmb x_i-y_i<-\varepsilon\}\]也就是只将对求导结果有影响的数据(预测与实际值误差大于$\varepsilon$)取出来进行求导。L2-loss目标函数有梯度,这是因为目标函数一阶可微;而函数不是二阶可微的,这代表黑塞矩阵$\nabla^2f(\pmb w)$不存在。因此有人(Mangasarian)提出该问题下的广义黑塞矩阵。令$I=I_1\cup I_2$,广义黑塞矩阵定义:
\[\nabla^2f(\pmb w)=I+2C(X_{I,:})^TD_{I,I}X_{I,:}\]$I$是单位矩阵,而$D_{l\times l}$是对角矩阵,满足
\[D_{ii}=\begin{cases} 1&\text{if }i\in I\\ 0&\text{else} \end{cases}\]这样的设置不难理解,对l2-loss逐步求导的过程如下:
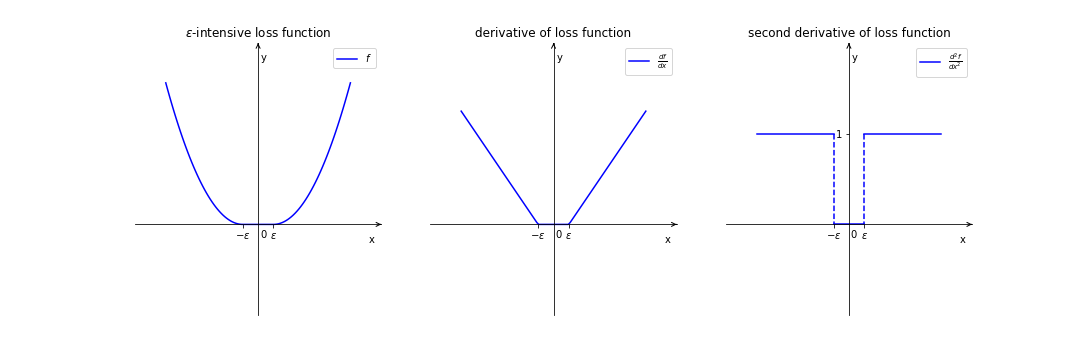
在求二阶导时,只有$\varepsilon$和$-\varepsilon$这两点处不可微,而考虑到数据点落到这两点的概率极小,所以可以刨去这两点去求导。由于黑塞矩阵很大($l\times l$),因此将这样的矩阵存储是不合理的。和之前一样,LIBLINEAR采用Hessian-free的方法,只计算黑塞矩阵和向量的乘积:
\[\nabla^2f(\pmb w)\pmb v=\pmb v+2C(X_{I,:})^T(D_{I,I}(X_{I,:}\pmb v))\]这样就能达到节省存储空间和提高算法运行速度的目的。
对偶坐标下降法
现在考虑用对偶坐标下降法(DCD)求解SVR问题。对每个分量的更新等价于求解子问题
\[\begin{aligned} \min_{z}\quad&f_A(\pmb\alpha+z\pmb e_i)-f_A(\alpha)=\nabla_if_A(\pmb \alpha)z+\frac12\nabla_{ii}^2f_A(\pmb\alpha)z^2\\ \text{s.t.}\quad&0\leq\alpha_i+z\leq U \end{aligned}\]其中$\pmb e_i$是长度为$2l$,第$i$个元素为1,其余元素为0的列向量,$z$的更新仍具有闭式解:
\[\alpha_i\gets\min(\max(\alpha_i-\dfrac{\nabla_if_A(\pmb\alpha)}{\nabla^2_{ii}f_A(\pmb\alpha)},0) ,U)\]其中
\[\nabla_if_A(\pmb\alpha)=\begin{cases} \big(Q(\pmb\alpha^+-\pmb\alpha^-)\big)_i+\varepsilon-y_i+\lambda\alpha_i^+,&\text{if }1\leq i\leq l\\ -\big(Q(\pmb\alpha^+-\pmb\alpha^-)\big)_{i-l}+\varepsilon+y_{i-l}+\lambda\alpha_{i-l}^-.&\text{if }l+1\leq i\leq2l \end{cases}\]黑塞矩阵也很好求:
\[\nabla_{ii}^2f_A(\pmb\alpha)=\begin{cases} \bar{Q}_{ii}&\text{if }1\leq i\leq l\\ \bar{Q}_{i-l,i-l}&\text{if }l+1\leq i\leq 2l \end{cases}\]显然黑塞矩阵可以在迭代开始前就求好,后面直接取用即可;此外,和求解SVC一样,SVR也存在更新前后$\alpha_i$原地踏步的情况,因此提前判别并直接进行下一轮更新可以减少计算量;最后,我们可以设置并维护一个向量$\pmb u$:
\[u=\sum_{i=1}^l(\alpha_i^+-\alpha_i^-)\pmb x_i\]这样可以在求解结束后直接返回最优的$\pmb w$,还可以减少$(Q(\pmb\alpha^+-\pmb\alpha^-))_i$的计算量,因为
\[(Q(\pmb\alpha^+-\pmb\alpha^-))_i=\pmb u^T\pmb x_i\]SVR下的DCD算法如下:

改进的对偶坐标下降法
该算法将$\pmb\alpha$中$2l$个变量看作是独立的,但实际上,考虑拉格朗日对偶性的KKT条件,若$\pmb\alpha$是最优的,则必有
\[\alpha_i^+\alpha_i^{-}=0,\forall i\]也就是$\alpha_i^+$和$\alpha_i^-$至少有一个为0。如果它们俩其中一个为正,那么另一个十分有可能在最后的循环中一直为0,所以会有很多检查时间被浪费(被浪费的没有更新时间,因为这些变量需要先判别后更新,而算法会将它们判别不需要更新,因此只有判别时间被浪费)。因此,DCD算法在SVR问题上可以进一步优化。
考虑上面的最优性条件,可以将对偶问题目标函数中的$(\alpha_i^+)^2+(\alpha_i^-)^2$修改为$(\alpha_i^+-\alpha_i^-)^2$:
\[\min_{\pmb\alpha^+,\pmb\alpha^-}\quad\frac12(\pmb\alpha^+-\pmb\alpha^-)^TQ(\pmb\alpha^+-\pmb\alpha^-)+\sum_{i=1}^l\bigg(\varepsilon(\alpha_i^++\alpha_i^-)-y_i(\alpha_i^+-\alpha_i^-)+\frac\lambda2(\alpha^{+}_i-\alpha^-_i)^2\bigg)\\\]由于我们在DCD算法中时刻保持$\alpha_i^+\geq0,\alpha_i^+\geq0$,因此在最优点处,我们有
\[\alpha_i^++\alpha^-_i=\vert\alpha_i^+-\alpha_i^-\vert\]定义$\pmb\beta=\pmb\alpha^+-\pmb\alpha^-$,对偶问题可以被改写为
\[\min_{\pmb\beta}\quad f_{B}(\pmb\beta)\\ \text{s.t.}\quad-U\leq\beta_i\leq U,\forall i\]其中
\[f_B(\pmb\beta)=\frac12\pmb\beta^T\bar{Q}\pmb\beta-\pmb y^T\pmb\beta+\varepsilon\Vert\pmb\beta\Vert_1\]如果$\pmb\beta^*$是上述优化问题的最优解,那么
\[(\alpha_i^+)^*=\max(\beta_i^*,0),(\alpha_i^-)^*=\max(-\beta_i^*,0)\]现在考虑该优化问题的求解,还是使用坐标下降法,对第$i$个分量进行更新等价于求解子问题:
\[\min_{s}\quad g(s)\\ \text{s.t.}\quad-U\leq s\leq U\]其中
\[\begin{aligned} g(s) &=f_B(\pmb\beta+(s-\beta_i)\pmb e_i)-f_B(\pmb\beta)\\ &=\varepsilon\vert s\vert+(\bar{Q}\pmb\beta-\pmb y)_i(s-\beta_i)+\frac12\bar{Q}_{ii}(s-\beta_i)^2+\text{constant} \end{aligned}\]分类讨论$g(s)$的导数:
\[\begin{cases} g'_p(s)=\varepsilon+(\bar{Q}\pmb\beta-\pmb{y})_i+\bar{Q}_{ii}(s-\beta_i),&\text{if }s\geq0\\ g'_n(s)=-\varepsilon+(\bar{Q}\pmb\beta-\pmb{y})_i+\bar{Q}_{ii}(s-\beta_i),&\text{if }s\leq0\\ \end{cases}\]显然两个导函数都是$s$的线性函数,且
\[g_n'(s)\leq g_p'(s),\forall s\in\mathbb{R}\]当$g’(s)=0$时,$g(s)$取最小值。一共三种情况,如下图所示:
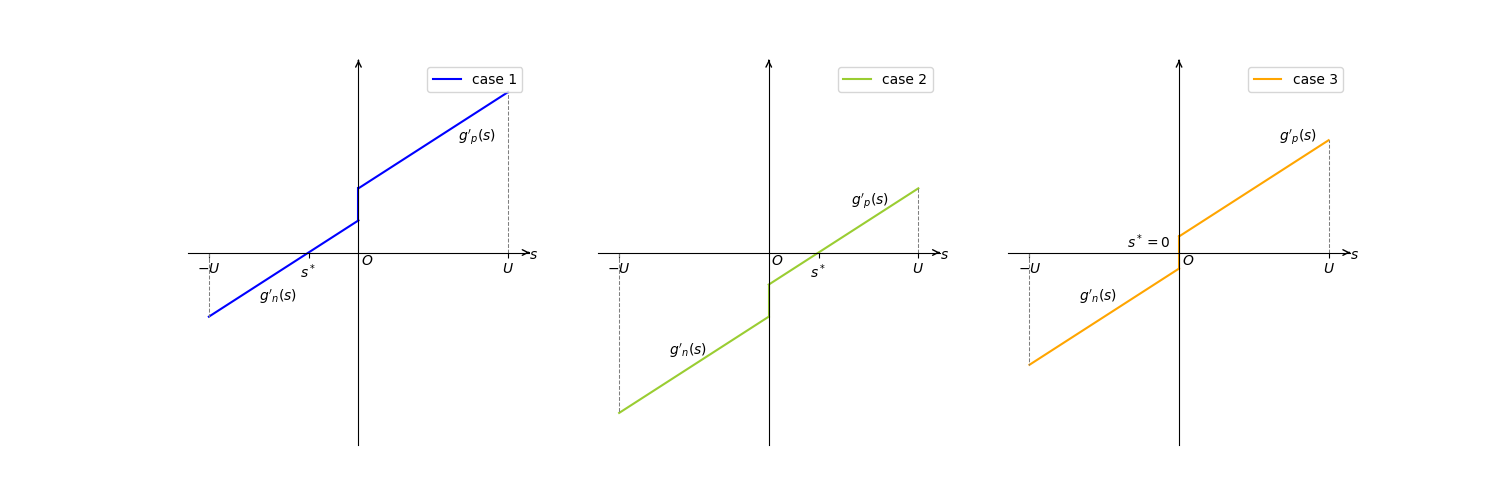
可以得到三种情况下$s^*$的闭式解:
\[s\gets\max(-U,\max(U,\beta_i+d))\]其中
\[d=\begin{cases} -\dfrac{g'_p(\beta_i)}{\bar{Q}_{ii}}&\text{if }g’_p(\beta_i)<\bar{Q}_{ii}\beta_i\\ -\dfrac{g'_n(\beta_i)}{\bar{Q}_{ii}}&\text{if }g’_n(\beta_i)>\bar{Q}_{ii}\beta_i\\ -\beta_i&\text{otherwise} \end{cases}\]到这里,就可以总结出SVR问题下的DCD改进算法:

类似的,我们还是维护$\pmb u$向量作为解。论文的后面是关于算法收敛性的讨论,算法实现上的细节以及实验。我们这里只提一下算法实现中的Shrink过程:它会衡量各分量违反最优性的程度,对于违反程度不大的分量,算法会将其忽视,只对剩下的分量进行更新,由此达到提高算法效率的目的。具体过程可以参考原论文。