SVR在线性函数两侧制造了一个“间隔带”,间距为$\varepsilon$(也叫容忍偏差,是一个由人工设定的经验值),对所有落入到间隔带内的样本不计算损失,也就是只有支持向量才会对其函数模型产生影响,最后通过最小化总损失和最大化间隔来得出优化后的模型:
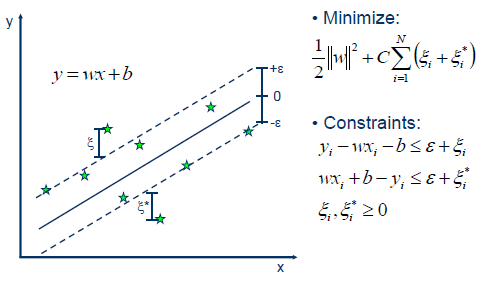
我们这里忽略从原问题到对偶问题的推导,直接给出对偶问题:
\[\begin{aligned} \min_{\pmb{\alpha},\pmb{\alpha}^*}\quad&\dfrac12(\pmb{\alpha}-\pmb{\alpha}^*)^\top Q(\pmb{\alpha}-\pmb{\alpha}^*)+\varepsilon\sum_{i=1}^l(\alpha_i+\alpha_i^*)+\sum_{i=1}^l z_i({\alpha}_i-{\alpha}_i^*)\\ \text{subject to}\quad&\pmb e^\top(\pmb{\alpha}-\pmb{\alpha}^*)=0\\ &0\leqslant\alpha_i,\alpha^*_i\leqslant C,i=1,\cdots ,l \end{aligned}\]可以看出该问题和之前分类问题的对偶问题:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^\top Q\pmb\alpha-\pmb{e}^\top\pmb{\alpha}\\ \text{subject to}\quad& \pmb{y}^\top\alpha=0,\\ &0\leqslant\alpha_i\leqslant C,i=1,\cdots ,l \end{aligned}\]形式上差别较大,我们不禁怀疑适用于分类SVM的SMO算法对回归问题是否同样有效。这里笔者通过一些变换来证明回归问题的对偶问题仍可以用SMO算法来解决,并给出适用于SMO算法的问题的格式。
这是在阅读libsvm源码时得到的启发:我们将$\alpha$和$\alpha^*$这两个列向量拼接起来:
\[\pmb\beta=\begin{bmatrix} \pmb\alpha\\\pmb\alpha^* \end{bmatrix}\]之后我们便可以将优化问题改为只含$\beta$的形式:
\[\begin{aligned} f&=\dfrac12(\pmb{\alpha}-\pmb{\alpha}^*)^\top Q(\pmb{\alpha}-\pmb{\alpha}^*)+\varepsilon\sum_{i=1}^l(\alpha_i+\alpha_i^*)+\sum_{i=1}^l z_i({\alpha}_i-{\alpha}_i^*)\\ &=\frac12\pmb\beta^\top\begin{bmatrix} Q&-Q\\ -Q&Q \end{bmatrix}\pmb\beta+\begin{bmatrix} \varepsilon+\pmb z\\ \varepsilon-\pmb z\\ \end{bmatrix}_{2l\times1}^\top\pmb\beta \end{aligned}\]类似的,约束条件也可以改写:
\[\begin{bmatrix} \pmb{e}^\top&-\pmb e^\top \end{bmatrix}\pmb\beta=0,0\leqslant\beta_i\leqslant C\]因此,经过变换之后的SVR对偶问题,仍然是一个SMO可解决的问题,就像SVC一样,因为其满足这样的格式:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^\top Q\pmb\alpha+\pmb{p}^\top\pmb{\alpha}\\ \text{subject to}\quad& \pmb{y}^\top\alpha=0,\\ &0\leqslant\alpha_i\leqslant C,i=1,\cdots ,l \end{aligned}\]在分类问题中,$\pmb y_i=1$当且仅当$\pmb x_i$样本为正类,$\pmb y_i=-1$当且仅当$\pmb x_i$样本为负类;而在回归问题中,$\pmb y$也是一个非1即-1的向量:
\[\begin{bmatrix} \pmb e\\ -\pmb e \end{bmatrix}\]也就是前$l$个元素为1,后$l$个元素为-1;分类问题中,$\pmb p$向量是一个全-1向量,而在回归问题中则是
\[\begin{bmatrix} \varepsilon +z_1\\ \vdots\\ \varepsilon +z_l\\ \varepsilon-z_1\\ \vdots\\ \varepsilon-z_l\\ \end{bmatrix}\]其中$z_i$为第$i$个样本对应的标签值;分类问题中的Q矩阵为
\[Q_{ij}=y_iy_jK(\pmb x_i,\pmb x_j)\]其中$y_i$为第$i$个样本的标签,后面的$K(\pmb x_i,\pmb x_j)$可以是样本间的内积(线性SVM),也可以是核函数操作后的结果。在变换之前的对偶问题中,回归问题的Q矩阵为
\[Q_{ij}=K(\pmb x_i,\pmb x_j)\]变换后的新Q矩阵为四个矩阵的拼接:
\[Q^{new}=\begin{bmatrix} Q&-Q\\ -Q&Q\\ \end{bmatrix}\]仔细观察就可以发现,变换之后的Q矩阵和分类问题中的Q矩阵定义形式上类似:
\[Q^{new}_{ij}=y_iy_jK(\pmb x_{i\mod l},\pmb x_{j\mod l})\]这里需要取余操作,因为$i=1,\cdots,2l$,而样本只有$l$个。由此,我们揭示了回归问题用SMO算法求解的可行性。