背景
对于Sigmoid函数
\[f(x)=\frac{1}{1+e^{-x}}\]有一个很好的性质
\[\dfrac{\partial f}{\partial x}=f\cdot(1-f)\]对于多元广播的Sigmoid函数
\[\pmb f=\begin{bmatrix} f_1&f_2&\cdots&f_n \end{bmatrix}\]对其求导,根据多元函数求导法则,结果应该是一个矩阵,且是一个对角矩阵:
\[\dfrac{\partial\pmb f}{\partial\pmb x}=\begin{bmatrix} \dfrac{\partial f_i}{\partial x_j} \end{bmatrix}_{ij}=\begin{bmatrix} f_1(1-f_1)&&\\ &\ddots&\\ &&f_n(1-f_n) \end{bmatrix}\]在神经网络中,Sigmoid函数常常被作为激活函数使用
\[\pmb x_{k+1}=\text{Sigmoid}(\pmb x_{k}W_k+\pmb b_k)\]其中$\pmb x_{k+1},\pmb x_k$分别为输入数据在神经网络第$k$层和第$k+1$层的值,$W_k$和$\pmb b_k$分别是第$k$层的权重矩阵和偏置向量。以上式为例,在反向传播过程中,我们利用链式法则计算偏导。对于每一条数据,都会有上面这样的一个偏导矩阵,而在数据向量化的背景下,我们一次常常对多个数据计算梯度,那么此时形成的就是一个$n\times d\times d$的多维矩阵,也就是张量,其中$n$是一次性处理的数据量,$d$就是数据维数。
反向传播先得到的是一批数据的$\pmb f$,它是$n\times d$的,本文的目的就是在Python语言中寻找一种快速将一个$n\times d$矩阵$A$转化为$n\times d\times d$的张量$B$的方法,其中$B$的第$i$行元素是一个$d\times d$的对角阵,其对角元素正是矩阵$A$的第$i$行。
一种朴素的想法
最基本的想法就是,利用for循环和Numpy的diag函数实现:
import numpy as np
n, d = 4, 3
A = np.arange(n * d).reshape(n, d)
B = np.zeros((n, d, d))
for i in range(n):
B[i] = np.diag(A[i])
也就是对$B$的每一行循环赋值。我们知道,Python中的for循环是很耗时的,而Numpy的数据向量化处理在Python中可以提高运行效率,这是因为Numpy将运算中无可避免的for循环放在C中处理,处理时间自然缩减。那么我们能否用向量化的思想达成我们的目标呢?
深入numpy.diag的实现
给定一个长度为$n$的一维数组,numpy.diag函数可以返回一个对角元为该数组的矩阵;给定一个二维数组,numpy.diag则返回一个一维数组,元素为其对角元。假如我们想实现第一种功能,大概率是这样书写函数:
def diag(arr):
l = len(arr)
ret = np.zeros((l, l))
for i in range(l):
ret[i][i] = arr[i]
return ret
但当我们打开该函数的源码时,发现事情并没有那么简单:
def diag(v, k=0):
# 这里删除了注释
v = asanyarray(v)
s = v.shape
if len(s) == 1:
n = s[0] + abs(k)
res = zeros((n, n), v.dtype)
if k >= 0:
i = k
else:
i = (-k) * n
res[:n - k].flat[i::n + 1] = v
return res
elif len(s) == 2:
return diagonal(v, k)
else:
raise ValueError("Input must be 1- or 2-d.")
重点考察len(s)==1的情形,也就是输入为一维数组,生成对角矩阵。这里的默认参数k表示对角线的位置,大于零位于对角线上面,小于零则在下面。比如diag([1, 2, 3], 1)生成的是
array([[0, 1, 0, 0],
[0, 0, 2, 0],
[0, 0, 0, 3],
[0, 0, 0, 0]])
而diag([1, 2, 3], -1)对应的是
array([[0, 0, 0, 0],
[1, 0, 0, 0],
[0, 2, 0, 0],
[0, 0, 3, 0]])
由于本文讨论的问题不涉及k不为0的情况,因此我们将这里的代码进行缩减:
def diag(v):
s = v.shape
n = s[0]
res = np.zeros((n, n), v.dtype)
res.flat[::n + 1] = v
return res
在这里,diag将待返回数组展开(flat),然后利用ndarray的高级索引,对res进行赋值。
举例来说,我们调用
diag([1, 2, 3])
来创建对角阵X
array([[1, 0, 0],
[0, 2, 0],
[0, 0, 3]])
我们将其展开成一维数组x
array([1, 0, 0, 0, 2, 0, 0, 0, 3])
可以注意到对角元素在x上距离是相同的,都是矩阵的尺寸n加上1,因此我们将这些位置的元素依次赋予v对应的值:
res.flat[::n + 1] = v # 从头到尾,步长为n+1
比如这个例子里就是
res[0] = v[0]
res[4] = v[1]
res[8] = v[2]
Numpy将上面的多个语句利用高级索引缩成了一句。
设计新的方法
受到numpy.diag的启发,我们可以将待返回的三维张量和输入的二维数组展开,利用高级索引,对展开张量指定的位置赋值。
比如输入的二维数组是
array([[0, 1, 2],
[3, 4, 5]])
我们希望生成的张量为
array([[[0., 0., 0.],
[0., 1., 0.],
[0., 0., 2.]],
[[3., 0., 0.],
[0., 4., 0.],
[0., 0., 5.]]])
它的展开为
array([0, 0, 0, 0, 1, 0, 0, 0, 2, 3, 0, 0, 0, 4, 0, 0, 0, 5])
观察待修改元素的位置,索引分别为0, 4, 8, 9, 13, 17。可以发现我们只需要确定前3元素的位置,也就是0,4,8即可,后面元素的索引都是这三个索引加上单个对角矩阵大小($d^2$)的整数倍即可。我们可以利用广播加法得到我们想要的索引:
a = np.array([0, 4, 8]) # 第一个矩阵待修改的位置
b = np.array([0, 9]) # 9为矩阵大小,上一个矩阵待修改的位置加上9之后就是下一个矩阵的相同位置
index = (b.reshape(-1, 1) + a).reshape(-1)
这样得到的index为
array([ 0, 4, 8, 9, 13, 17])
正是待修改的元素位置索引。
由此我们可写出我们期望功能的函数:
def tensor_diag(x):
# x是二维数组
n, d = x.shape
ret = np.zeros((n, d, d))
index = (np.arange(0, n * d * d, d * d).reshape(-1, 1) +
np.arange(0, d * d, d + 1)).reshape(-1)
ret.flat[index] = y.reshape(-1)
return ret
我们对函数进行测试
x = np.arange(6).reshape(2, 3)
y = tensor_diag(x)
print("x :\n", x)
print("y :\n", y)
输出
x :
[[0 1 2]
[3 4 5]]
y :
[[[0. 0. 0.]
[0. 1. 0.]
[0. 0. 2.]]
[[3. 0. 0.]
[0. 4. 0.]
[0. 0. 5.]]]
发现我们设计的函数很好的实现了我们的要求。
时间比较
在最后,我们比较新方法相比于之前的循环计算,是否有效率上的改进。
我们设置不同的$d$与$n$,测试在不同大小数据下,两种算法处理时间的区别:
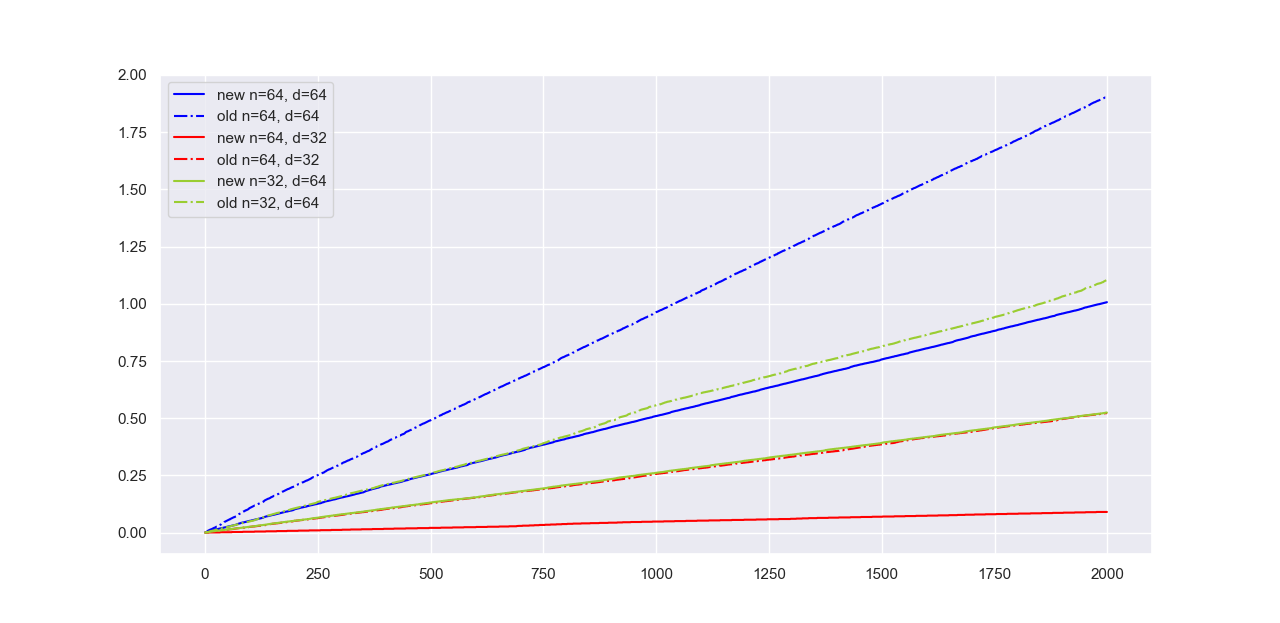
可以发现我们设计的新计算方法在各种条件下,相比于笨拙的循环,都有至少一倍的性能提升。此外,这一提升在$n$相比于$d$较大(红色曲线)时更为明显(提升了至少三倍),显然是因为我们避免了Python中较多的for循环。
总结
在数个月前,笔者利用Numpy实现神经网络时,便遇到了批量计算求导结果的对角矩阵时耗时过长的问题,但当时并没有深入到diag函数计算的原理,导致问题被拖延下来。最近重拾过去的工作,使得我重新思考这个问题,并终于给出了一个较好的解决方案。