原文链接:https://arxiv.org/pdf/1711.03705.pdf.
Introduction
在这篇文章中,作者希望将深度学习应用到在线学习的场景中,称其为“在线深度学习”。在线深度学习的挑战主要就是如何为特定任务指定网络深度:
- 网络太深:由于在线学习的特性,每次只得到一个样本,使得神经网络很难收敛,以及梯度消失问题;
- 网络太浅:模型的表达能力很弱,极限的场景就是一个线性分类器。
本文提出了一个改良后的神经网络:Hedge Neural Network。它采用一种特殊的反向传播方式,称作Hedge Backpropagation,通过集成学习的思路,充分利用各个网络层的信息。
Preliminaries
在正式介绍Hedge网络之前,我们先介绍Hedge算法,这是一个年代很久远的算法,[Freund & Schapire, 1997] 从它推导出Adaboost算法。简单的说,在在线学习场景中,我们有$N$个专家,以及一个对应的权重向量$\textbf{x}^t\in[0,1]^N$,其中$\sum_{i=1}^Nw_i^t=1$。每一轮我们的决策是专家建议的加权输出。当接受到正确答案后,我们基于每个专家收到的损失进行调整:

其中$\beta\in[0,1]$是调整损失的参数。
Model
接下来我们来介绍Hedge网络,网络结构如下图所示:
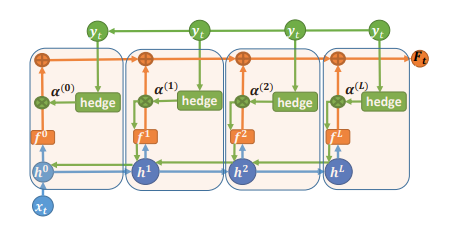
对于$L$层Hedge网络,它利用了网络每一层的输出。每一层的输出对应了一个线性分类器。最后的预测是根据每一层对应的线性分类器进行加权组合。将上述过程形式化:
\[\textbf{F}(\textbf{x})=\sum_{l=0}^L\alpha^{(l)}\textbf{f}^{(l)}\]其中
\[\begin{aligned} \textbf{f}^{(l)}&=\text{softmax}(\textbf{h}^{(l)}\Theta^{(l)}),i=0,\cdots,L\\ \textbf{h}^{(l)}&=\sigma(W^{(l)}\textbf{h}^{(l-1)}),i=1,\cdots,L\\ \textbf{h}^{(0)}&=\textbf{x} \end{aligned}\]参数更新上
-
线性分类器
采用梯度下降:
\[\begin{aligned} \Theta_{t+1}^{(l)}&\gets\Theta_{t}^{(l)}-\eta\nabla_{\Theta_{t}^{(l)}}\mathcal{L}(\textbf{F}(\textbf{x}_t),y_t)\\ &=\Theta_{t}^{(l)}-\eta\alpha^{(l)}\nabla_{\Theta_{t}^{(l)}}\mathcal{L}(\textbf{f}^{(l)},y_t) \end{aligned}\] -
网络参数
采用梯度下降:
\[W^{l}_{t+1}\gets W_t^{l}-\eta\sum_{j=1}^L\alpha^{(j)}\nabla_{W^{(l)}}\mathcal{L}(\textbf{f}^{(j)},y_t)\] -
权重参数
采用Hedge算法:
\[\alpha_{t+1}^{(l)}\gets\alpha_{t}^{(l)}\beta^{\mathcal{L}(\textbf{f}^{(l)},y)}\]
完整的算法:

Experiments
本文的实验数据集主要是二分类的:
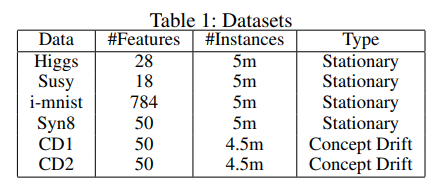
其中还有两个Concept drift数据集,因为作者认为模型能够应付该问题:Concept drift发生后,网络会自适应调整$\alpha$。
作者考察了不同深度,不同数据量下的模型表现:

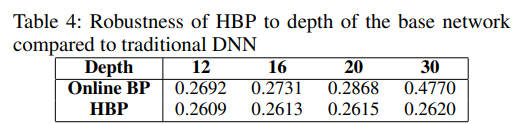
此外还考察了模型的鲁棒性:
Conclusion
HBP使用对冲策略,从不同的隐藏层的多个输出进行预测对网络进行了改进,并对反向传播算法进行了修改,以允许知识在更深层次和更深层次之间共享浅网络。这种方法自动识别如何以及何时修改一个有效的网络容量数据驱动方式,基于观察到的数据复杂性。文章通过在大型数据集上的大量实验验证了所提出的方法。