原文获取:https://ieeexplore.ieee.org/document/8594923.
背景介绍
在这里,我们面临这样一个场景:城市规划者希望从历史数据中学习,特殊情况(如事件或节日)如何与交通流中的不寻常模式相关,以支持改进对事件和交通系统布局的规划。因此,我们应该考虑在一定的时间间隔内观察到的交通流值的序列。这样的流序列可以被建模为流的概率分布。本文采用一种离群值检测方法,即局部离群值因子(LOF)来处理流量分布,而不是单个观测。我们应用离群值检测在线扩展数据库,采用新的流分布。
本文的几个贡献:
- 流量集合可以被表示成概率分布;
- 建立一个框架,用以处理历史数据(流概率分布)中的异常值;
- 提出了一种通过考虑流量分布的时间信息来构建历史流量概率分布数据库的策略;
- 提出了一种局部离群因子(LOF)算法的改进:FPD-LOF,通过采用巴塔查里亚相似度度量(巴氏距离)来检测流概率分布离群值;
- 将FPD-LOF应用于一种特殊的情况,以便与现有的方法进行比较。实验分析表明,FPD-LOF的性能优于目前最先进的流异常值检测算法;
- 通过样例,揭示了基于巴氏距离的FPD-LOF算法能够找到与异常天气、特殊事件相关联的异常点。
问题描述
本文的重点是检测出流概率分布的异常。一个交通流(Traffic flow)被定义为在给定时间区间内,通过某一地点(比如城市道路网络中的一点)的车辆数量。而一个流概率分布(Flow probability distribution, FPD)将流量值与在给定时间内发生的可能性联系起来。
令$I$是一个时间区间中的时间点集合。每个时间点对应记录了某一点的流量$X=[x_1,\cdots,x_{\vert I\vert}]$。令$\lambda$为为两不重合时间点之间的时间,$\delta$为每个时间点对流量的测量时间。我们假定$\lambda=\delta$,即测量的流量不会重合。
从$I$中我们可以提取一个集合$\mathcal{T}=\{T_1,\cdots,T_\tau\}$,其中每一个元素是$\mu$个连续时间点(也是一个集合)。对于$T_j,j=1,\cdots,\tau$,我们定义这个连续时间点开始于$\iota(T_j)$,那么
\[T_j=\{\iota(T_j),\iota(T_j)+1,\cdots,\iota(T_j)+\mu\}.\]接着定义$X_{T_j}$为$T_j$这段时间的流量值。举例来说,假如$\lambda=\delta=1h$,$\tau=7$,$\forall j=1,\cdots,7$,$\iota(T_j)=7:00$,而$\mu=3$,那么$\mathcal{T}$可以是一个星期七天,每天7:00-10:00的流量。
对于每个集合$X_{T_j}$,它都可以被表示为离散随机变量$Y_j\in N_0$,从而有一个分布函数$f_{Y_j}=f_j$,我们直接用频率去估计:
\[f_j(y)\approx\hat{f}_j(y)=\dfrac{|\{x=y|x\in X_{T_j}\}|}{|X_{T_j}|}=\dfrac{|\{x=y|x\in X_{T_j}\}|}{\mu}\]定义这样的概率密度分布为流概率分布 (FPD)。由此定义FPD异常:给定一个经验流概率分布族
\[F=\{\hat{f}_1,\hat{f}_2,\cdots,\hat{f}_\tau\}\]它是从$\{X_{T_1},\cdots,X_{T_\tau}\}$中导出。给定一个打分函数$s:F\to{R}$和一个阈值$\theta$,异常点(outliers)被定义为下面的集合:
\[O=\{\hat{f}_j\in F\vert s(\hat{f}_j)\geq\theta\}\]改进LOF实现FPD目标检测
现在考虑将概率分布变成可学习数据。文中做了一个简单的处理,比如有两个$\hat{f}:\hat{f_1},\hat{f_2}$:它们的概率密度函数用直方图绘制如下:
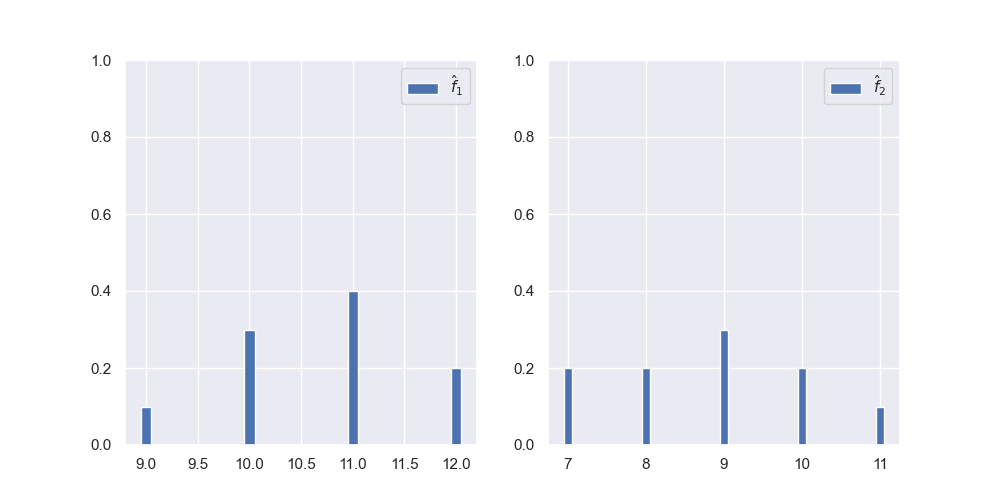
那么我们会取它们中最大的流量值作为特征值的最大值,从而将特征进行归一化。此时上面两个数据被变换成
\[\begin{aligned} \mathcal{A}_1&=\begin{bmatrix} 0&0&0&0&0&0&0&0&0&0.1&0.3&0.4&0.2 \end{bmatrix}\\ \mathcal{A}_2&=\begin{bmatrix} 0&0&0&0&0&0&0&0.2&0.2&0.3&0.2&0.1&0 \end{bmatrix}\\ \end{aligned}\]直方图如下:
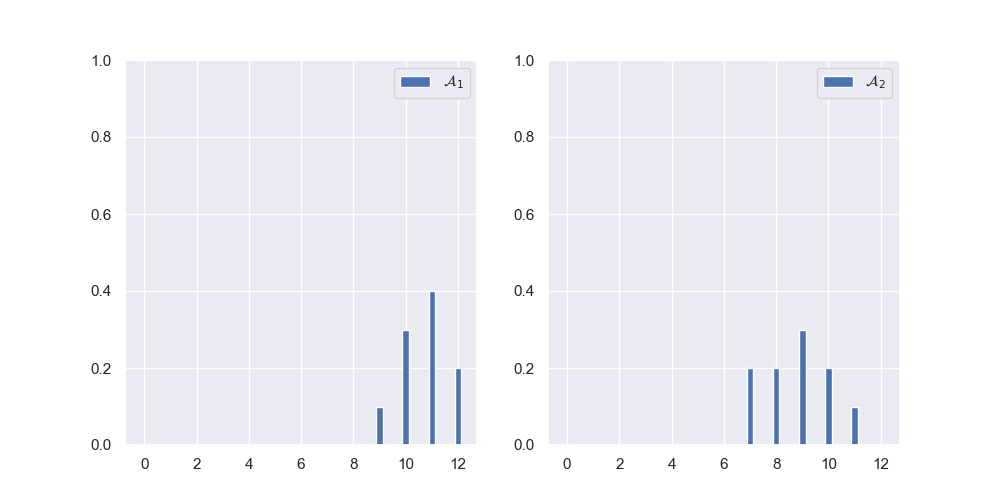
也就是一共13个特征。现在定义两个分布的距离,本文选择了巴氏距离,对于巴氏距离,它在统计学中用于测量两种离散概率分布的可分离性。在直方图相似度计算时,巴氏距离获得的效果最好,但计算是最为复杂的。定义如下:
\[B(\mathcal{A}_i,\mathcal{A}_j)=-\ln\sum_{m=1}^{d_i}\sum_{k=1}^{d_j}\sqrt{|m-k|+(\mathcal{A}_i(m)\mathcal{A}_i(k))}\]但发现在维基百科等资料中,似乎没有取绝对值一项,而是
\[B(\mathcal{A}_i,\mathcal{A}_j)=-\ln\sum_{m=1}^{d_i}\sum_{k=1}^{d_j}\sqrt{\mathcal{A}_i(m)\mathcal{A}_i(k)}\]这样用NumPy的向量化能很快计算出来。
现在考虑FPD场景下的LOF算法:令
\[F=\{\hat{f}_1,\cdots,\hat{f}_\tau\}\]是一个FPD族,然后给定一个新的$\hat{f}$,和一个参数$k(k<\tau)$,这个是用来控制集合$k\text{NN}(\hat{f})\subseteq F$的,表示与$\hat{f}$最近邻的$k$个分布。同时定义$k\text{NN-}dist(\hat{f}_i)$,表示分布$\hat{f}_i$和距其第$k$近的分布的距离。
在LOF中,$k\text{NN-}dist$是密度估计的最基本成分。离群值是指相对于它们的$k$个最近邻,局部密度相对较低的对象。这些密度估计通常与欧氏空间有关。然而,LOF是基于距离的异常检测,我们当然可以将距离换成非欧氏距离,比如这里的巴氏距离。
定义局部可达密度(lrd):
\[\text{lrd}(\hat{f})=1\bigg/\dfrac{\sum_{\hat{f}_i\in k\text{NN}(\hat{f})}\text{reach}_k(\hat{f},\hat{f}_i)}{|k\text{NN}(\hat f)|}\]其中可达距离定义为
\[\text{reach}_k(p,o)=\max\{k\text{NN-}dist(o), dist(p,o)\}\]所以局部可达密度是局部可达距离均值的倒数,$\hat{f}$和它最近邻样本的距离大,那么局部可达密度就小。定义局部异常因子:
\[LOF(\hat{f})=\dfrac{1}{|k\text{NN}(\hat{f})|}\sum_{\hat{f}_i\in k\text{NN}(\hat{f})}\dfrac{\text{lrd}(\hat{f}_i)}{\text{lrd}(\hat{f})}\]这里采用了一个分式,因为如果单纯的使用局部可达密度来衡量一个点是否异常,会有一个问题,局部可达密度容易受到簇的密度的影响,当样本空间里存在多个密度不同的簇时,密度较大的簇它的局部可达密度会比较大,容易造成误判。而LOF的思想不仅仅是看它的绝对密度,而是看这个点和相邻点的相对密度。
文中采用1作为阈值,也就是如果$LOF(\hat{f})>1$,那么$\hat{f}$为异常点。
实验部分
本文实验的评价指标为F-score和ROC-AUC曲线下面积。
实验A:时间序列数据集
将FPD-LOF与BLOF算法进行比较,BLOF是时间序列上探测异常的算法。所使用的的几个数据集:
- EnronInc:1999-2002年Enron公司的邮件网络,Ground truth记录了公司历史上的重大事件,比如收入损失;
- Reality Mining:该数据集包含了麻省理工大学通过在其移动设备上预装的软件在50周内连续记录的通信流数据。每周时间流序列为三种关系:语音通话、短信和蓝牙扫描。Ground truth记录了记录了学期的休息时间、考试周和假期。
- TwitterWorldCup:该数据收集的数据包含了2014年世界杯6月12日至7月13日的相关数据。这些推文会被世界杯的流行标签或官方标签过滤,如#世界杯、#国际足联、#巴西等。Ground truth包括所有比赛中的进球、点球和伤病,至少包括以下一支著名球队(巴西、德国、阿根廷、荷兰、西班牙和法国)。
实验结果:
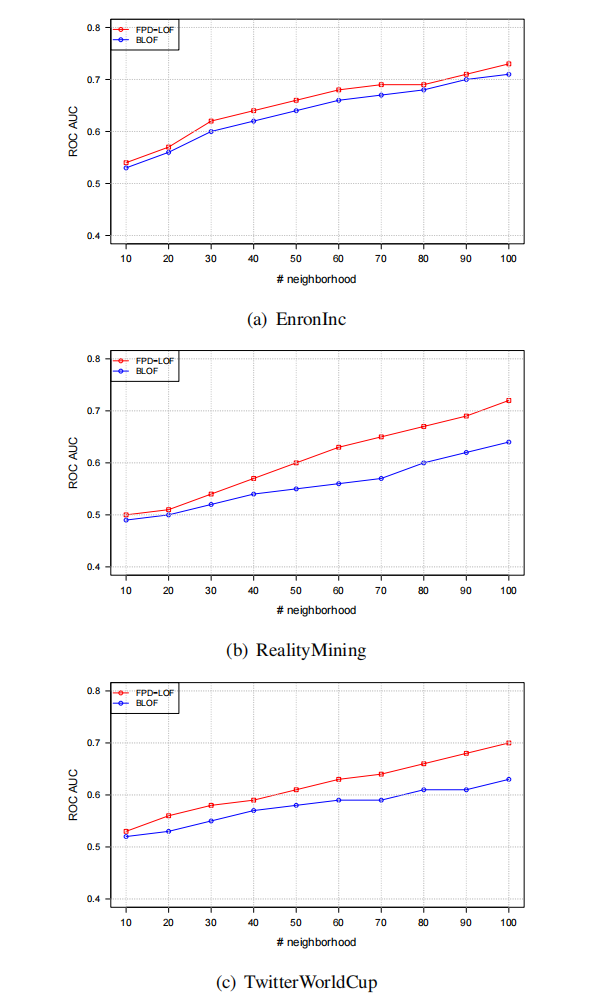
实验B:真实数据的定量分析
通过与欧登塞市的合作,作者团队得到了来自整个市区的几个测试地点的数据。每个数据输入都包含与在特定位置检测到的车辆相关的信息,例如:间隙、长度、日期、时间、速度和等级(即车辆类型)。在10个地点,传感器已经安装了基础设施。这10个地点具有不同的特征(交通密度、汽车或自行车计数器)。交通数据来自于2017年1月1日至2017年9月30日。
在使用新数据评估离群值检测技术时的一个常见问题是离群值没有被标记。为了便于对真实数据进行定量评估,文章向$F$中注入了合成的异常数据$f_i$,其长度$d^*=\max\{d_j\vert j=1,\cdots,\tau\}$。异常数据包括下面几种:
-
Null FPD:也就是空流,理解为街道一直是空的,$f_i(0)=1$;
-
Stable FPD:街道时刻的流量是一个定值,$f_i(x)=1$;
-
Regular FPD:可理解为均匀分布,所有的可能的流量值以相同概率发生:
\[f_i(m)=\frac1{d_i},m=1,\cdots,d^*\] -
Unexpected FPD:它模拟了当一个对交通流量产生强烈影响的异常事件发生时的行为(例如,导致某些道路关闭的节日或事故)所观察到的行为。它分为三个阶段:
\[f_i(m)=\begin{cases} \epsilon&\text{if }1\leq m\leq x\\ \Psi(m)&\text{if }x<m\leq y,m=1,\cdots,d^*\\ 0&\text{if }y<m\leq d^* \end{cases}\]其中$\Psi:[x,\cdots,y]\to[\epsilon,\cdots,(1-x\epsilon)]$是一个单增函数,且
\[\sum m\Psi(m)=(1-x\epsilon)\]即满足离散概率分布函数的条件。
-
Noise FPD,是依概率给原FPD加上白噪声,从$\mathcal{U}(0,1)$中采样一个$p$,然后指定一个阈值$\gamma_i$:
\[f_i=\begin{cases} f_i+n\sim\mathcal{N}(0,\sigma_i^2)&\text{if }p\geq\gamma_i\\ f_i&\text{otherwise} \end{cases}\]
我们绘制了前4种异常的示意图,相比于原文更精细:
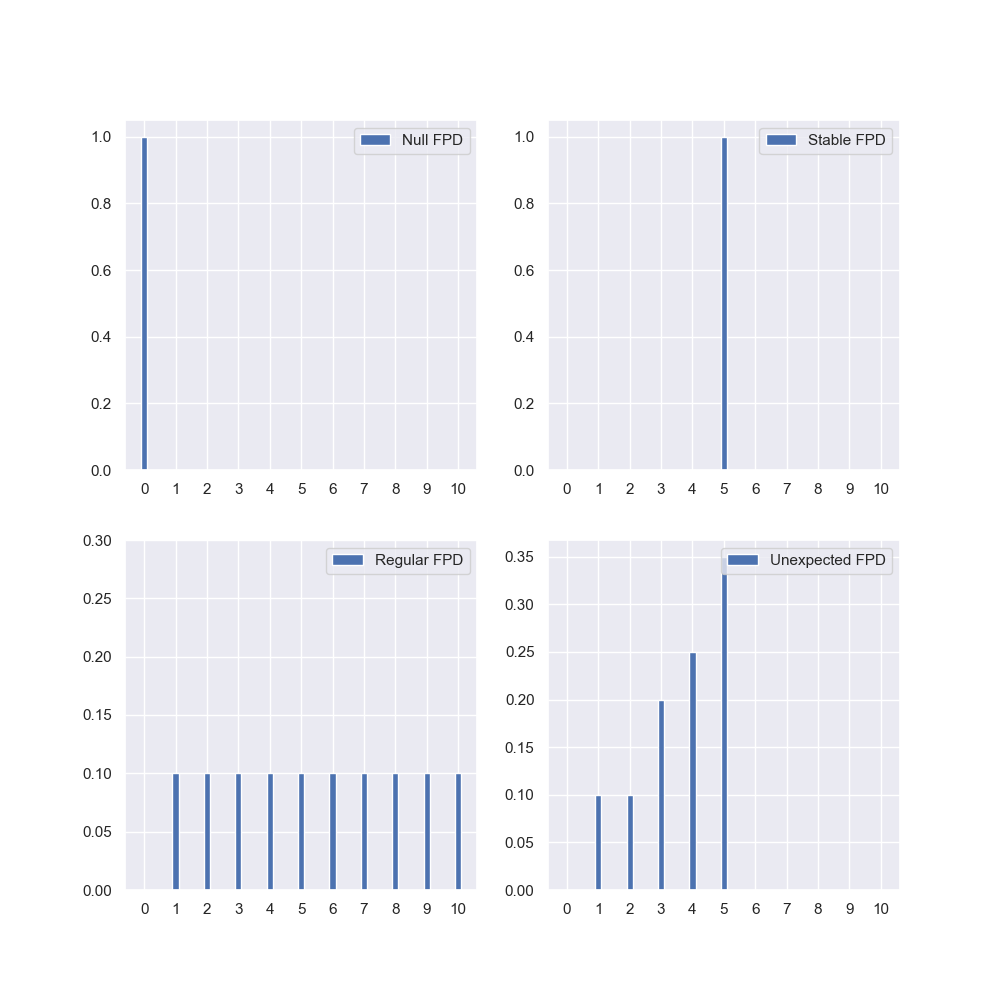
文章在最后做了一个case study:对每个数据集选出了最为异常的点(理解为LOF最大),然后根据Ground truth做出解释。
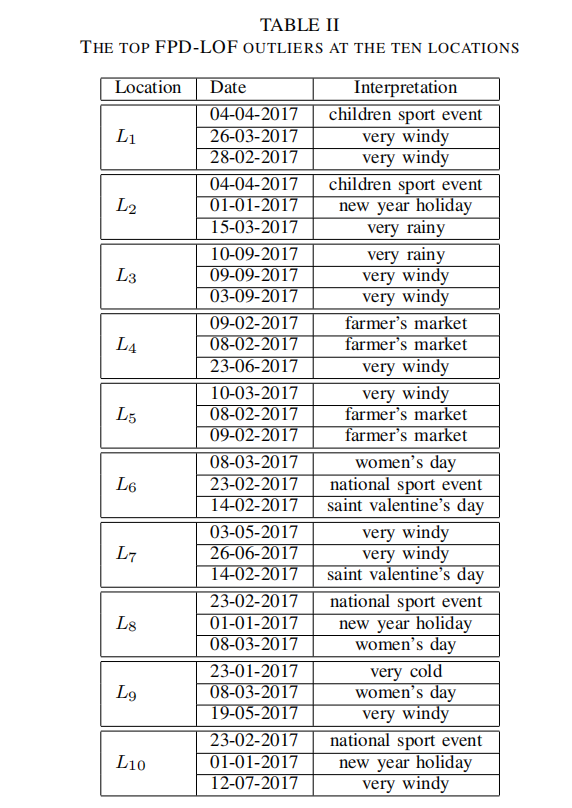
例如,2017年2月28日的FPD是一个异常值,因为天气风太大,乘坐汽车和公共汽车而不是自行车的人大幅增加。其他流异常值可能与重大事件有关。例如,一年的第一天(2017年01月01日)在三个地方都有很大的影响,庆祝妇女日(2017年08月03日)在三个地方都是异常值。我们可以用这样一个事实来证明第一个案例,即人们倾向于呆在家里,并在2016年昨晚的庆祝活动后进行一些重新设置。然而,我们可以通过女性在公共场所(餐馆、电影院、剧院等)庆祝节日来证明第二种情况。
总结
这是一篇交通流量+异常检测的文章,发在了2018年的ICDM上。本文的核心算法并不算新颖:LOF算法是2000年提出的,笔者主要在意的是本文是如何建模,以及如何进行实验:
- 建模上,本文将不同时间段的流量建模为离散分布,然后将分布转换成特征向量。然后基于距离和密度进行异常检测;
- 这篇文章的注意力放在的是单一位置上,然后只考虑时间上的异常,通常来源于特定事件或异常天气;
- 实验使用的是传统的分类指标,将检测出分布异常与此时Ground truth中异常事件的对应作为分类正确;
- 当我们手中只有流量数据,而没有Ground truth,我们如何判定异常检测的正确?文中构造出了几种异常FPD,比如街道是空的,街道流量始终是一个定值等。将它们注入到原数据集中。如果算法可以将这些人为合成的异常识别出来,那么算法可以算是有效的。