一维卷积的快速实现(2)

本文代码：https://github.com/Kaslanarian/FastConv.

本文记录笔者在PyDyNet中对高效实现CNN进行的探索，重点是采用im2col实现快速的一维二维的卷积和池化。im2col将卷积运算转换成矩阵乘积，它被很多深度学习框架，比如Caffe所采用。im2col方法搭配basic linear algebra subroutines (BLAS)和GPU能够极大加速CNN的训练速度。

一维卷积和二维卷积的朴素实现

这里快速过一遍按定义实现一维卷积核二维卷积，即依靠多重循环，这里以二维卷积为例，一维卷积的实现类似，只是少了一个循环。

import numpy as np


def shape_compute(n_h: int, n_w: int, k_h: int, k_w: int, stride: int,
                  padding: int):
    '''计算二维卷积下的输出特征数.

    Parameters
    ----------
    n_h : int
        输入数据的height特征数;
    n_w : int
        输入数据的width特征数;
    k_h : int
        卷积核在height方向的大小;
    k_w : int
        卷积核在width方向的大小.
    stride : int
        卷积步长;
    padding : int
        填充长度
    '''
    return (
        (n_h + 2 * padding - k_h) // stride + 1,
        (n_w + 2 * padding - k_w) // stride + 1,
    )


def conv2d_baseline(x: np.ndarray,
                    kernel: np.ndarray,
                    stride: int = 1,
                    padding: int = 0):
    '''用最基础的for循环实现二维卷积.

    Parameters
    ----------
    x : numpy.ndarray
        输入数据, 形状为(N, in_channels, n_h, n_w).
    kernel : numpy.ndarray
        卷积核，形状为(out_channels, in_channels, k_h, k_w)
    stride : int
        卷积步长;
    padding : int
        填充长度.
    '''
    assert x.ndim == 4, "输入数据的形状必须为(N, in_channels, n_h, n_w)."
    assert kernel.ndim == 4, "卷积核形状必须为(out_channels, in_channels, k_h, k_w)."
    N, in_channels, n_h, n_w = x.shape
    out_channels, _, k_h, k_w = kernel.shape
    assert _ == in_channels, "输入数据和卷积核的in_channels不同, {}!={}".format(
        in_channels, _)
    out_h, out_w = shape_compute(n_h, n_w, k_h, k_w, stride, padding)
    x = np.pad(
        x,
        [(0, 0), (0, 0), (padding, padding), (padding, padding)],
        'constant',
    )
    output = np.zeros((N, out_channels, out_h, out_w))
    for i in range(N):
        for j in range(out_channels):
            for k in range(out_h):
                for l in range(out_w):
                    for m in range(in_channels):
                        for row in range(k_h):
                            for col in range(k_w):
                                output[i, j, k,
                                       l] += x[i, m, k * stride + row,
                                               l * stride +
                                               col] * kernel[j, m, row, col]
    return output

Python中大量的循环导致程序效率低下(深入到计算机系统，就是JMP指令的频繁调用)，下面的程序运行超过了10秒：

x = np.random.randn(100, 3, 64, 64)
ker = np.random.randn(1, 3, 3, 3)
conv2d_baseline(x, ker)

一些不错的尝试

在接触到im2col方法前，我们也进行了自己的尝试，但都是程序上的优化，而不是算法上的：

用广播算法消除样本循环，通道循环和卷积核循环；
用scipy.ndimage中已实现好的correlate函数来对图片进行快速卷积。

细节参见一维卷积的快速实现。两种方法和im2col方法在不同场景下各有千秋，但im2col的优势在于它不需要我们手动编写卷积的反向传播规则。本文先讨论如何进一步优化一维卷积。

一维卷积的im2col

我们先来看一维卷积中的im2col，我们将问题简化，只考虑单样本，单通道的情况。以下面的卷积为例

\[\begin{bmatrix} x_1&x_2&x_3&x_4 \end{bmatrix}\star\begin{bmatrix} a_1&a_2 \end{bmatrix}=\begin{bmatrix} a_1x_1+a_2x_2&a_1x_2+a_2x_3&a_1x_3+a_2x_4 \end{bmatrix}\]

结果等价于

\[\bigg(\begin{bmatrix} x_1&x_2\\ x_2&x_3\\ x_3&x_4 \end{bmatrix}\begin{bmatrix} a_1\\a_2 \end{bmatrix}\bigg)^T=\begin{bmatrix} a_1x_1+a_2x_2\\a_1x_2+a_2x_3\\a_1x_3+a_2x_4 \end{bmatrix}^T\]

这样做的原理是，我们将输入数据每轮需要和卷积核进行运算的部分整理为矩阵的一行，其行数为输出尺寸，列数为卷积核尺寸。然后我们将卷积核整理为一列，卷积计算的是对应位置的乘积的和，而行向量与列向量相乘也是同样的效果，所以这样的变形是正确的。

用NumPy实现：

x = np.random.randn(20) # 输入数据
kernel_size = 3
kernel = np.random.randn(kernel_size) # 卷积核
out_features = len(x) + 1 - kernel_size # 计算输出长度

col = np.zeros((out_features, kernel_size))
for i in range(out_features):
    col[i] = x[i:i+kernel_size]
kernel = kernel.reshape(-1, 1)
result = (col @ kernel).T

现在将情景拓展到多样本，我们将左边的矩阵扩展为三维张量。我们在解析NumPy的广播机制时提到，如果是三维张量参与矩阵乘法，那么只有后面两个维度参与矩阵乘法，其余维度服从广播机制：

\[X_{N\times\text{n_output}\times\text{kernel_size}}Y_{\text{kernel_size}\times1}=Z_{N\times\text{n_output}\times1}\]

然后将$Z$的后两个轴进行转置即可：

kernel_size = 3
N = 100
x = np.random.randn(100, 20) # 输入数据，100个样本
kernel = np.random.randn(kernel_size) # 卷积核
n_output = x.shape[-1] + 1 - kernel_size # 计算输出长度

col = np.zeros((N, n_output, kernel_size))
for i in range(kernel_size):
    col[..., i] = x[:, i:i + n_output] # 这里进行了改进，即对kernel循环填充，减少循环次数
kernel = kernel.reshape(-1, 1)
result = (col @ kernel).transpose(0, 2, 1)

现在考虑多输入输出通道情景，输入数据和卷积核形状分别为

\[N\times\text{in_channels}\times\text{n_features},\text{out_channels}\times\text{in_channels}\times\text{kernel_size}\]

那么$X$的形状为$N\times\text{in_channels}\times\text{n_output}\times\text{kernel_size}$；$Y$的形状扩展成$\text{in_channels}\times\text{kernel_size}\times\text{out_channels}$。那么

\[XY=Z_{N\times\text{in_channels}\times\text{n_output}\times\text{out_channels}}\]

多通道输入时，卷积结果进行相加，所以将$Z$沿着$\text{in_channels}$求和，再将其沿着后面两个轴转置，就得到我们的目标输出，即形状为$N\times\text{out_channels}\times\text{n_output}$的数组张量。

# 自定义卷积运算的尺寸参数
N, in_channels, n_features = 100, 2, 20
out_channels, kernel_size = 3, 3

x = np.random.randn(N, in_channels, n_features)
kernel = np.random.randn(out_channels, kernel_size)
n_output = n_features + 1 - kernel_size

col = np.zeros((N, in_channels, n_output, kernel_size))

for i in range(kernel_size):
    col[..., i] = x[..., i:i + n_output]

col_filter = kernel.transpose(1, 2, 0)
out = col @ col_filter
result = out.sum(1).transpose(0, 2, 1)

用NumPy自动构造矩阵

一维卷积下im2col的要点之一就是用输入数据构造下面的矩阵（设输入特征数为$n$，卷积核大小为$k$）

\[\begin{bmatrix} x_1&\cdots& x_{k}\\ x_2&\cdots& x_{k+1}\\ \vdots&\ddots&\vdots\\ x_{n+1-k}&\cdots&x_{n} \end{bmatrix}\]

我们之前使用循环实现，这是最直接的想法。但有趣的是，NumPy提供了形成这样矩阵的方法。在介绍该方法之前，我们先来看NumPy数组的strides属性：

import numpy as np

x = np.arange(12).reshape(4, 3)
print(x.strides) # (24, 8)

strides，也就是步长，它是NumPy数组的一个属性（图源：Array Programming with NumPy，这篇文章是NumPy的综述，因为NumPy在各个自然科学领域的编程中起到极大的帮助，所以该文上了Nature）：

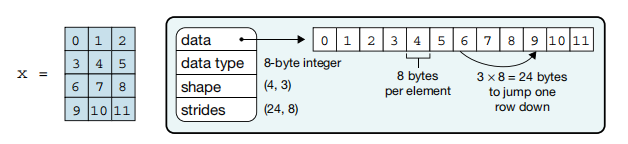
可以发现，NumPy数组的底层其实还是一维数组，只不过是其上层通过一系列API封装，使其在我们眼中有了形状的概念。学过C的读者可以将其等价于C中二维数组在内存中的连续存储。这里的strides属性，则是影响我们对数组元素的访问与修改。strides为(24, 8)，表明从数组的第$i$行第$j$列跳转到第$i+1$行第$j$列需要跨过24个字节，而从数组的第$i$行第$j$列跳转到第$i$行第$j+1$列需要跨越8个字节。这是因为：

数组x的单个元素占8个字节，即int，所以同行相邻列元素间相差8个字节；
数组x的列数为3，所以同列相邻行元素间相差3个元素，即24个字节.

可以发现strides受两个因素影响：数据类型和数组形状。

NumPy中提供了这样一个函数：np.lib.stride_tricks.as_strided，它能够通过修改步长将数组变成我们想要的样子。举个例子

>>> import numpy as np
>>> from numpy.lib.stride_tricks import as_strided
>>> x = np.arange(12)
>>> x
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
>>> y = as_strided(x, shape=(4, 3), strides=(x.itemsize, x.itemsize))
>>> y
array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4],
       [3, 4, 5]]) 
>>> y.strides
(8, 8)

x.itemsize是数组x单个元素所占的字节数，之所以这么写是因为我们发现，在Windows下x单个元素是4字节，在Ubuntu下是8字节，当然原因也可能是NumPy版本问题。

数组y是一个4行3列数组，同时它的同行相邻列元素间，以及同列相邻行元素间都之差8个字节，这就导致上面的结果，即x[i][j+1]和x[i+1][j]相等，这正是我们想要的。但值得注意的是，这个方法并没有对原数组x进行拷贝，x和y共享的是相同的内存，也就是上图中的data指针指向的内存：

>>> x[1] = 10
>>> y
array([[ 0, 10,  2],
       [10,  2,  3],
       [ 2,  3,  4],
       [ 3,  4,  5]])

可以发现y[0, 1]和y[1, 0]都变成10，这是因为这两个元素指向的是同一个内存地址，即x[1]的位置。但我们只需要得到矩阵乘积，而不涉及元素的更改，所以这一部分对我们的工作影响不大。

由此，我们可以写出数据矩阵转换的代码，不需要for循环：

# 原
for i in range(kernel_size):
    col[..., i] = x[..., i:i + n_output]
    
# 现
size = x.itemsize
col = np.lib.stride_tricks.as_strided(
    x,
    shape=(N, in_channels, n_output, kernel_size),
    strides=(size * in_channels * n_features, 
             size * n_features, 
             size * stride, # 考虑了步长
             size
    )
)

实验

我们执行这样的实验：控制N=100, in_channels=3, out_channels=2, kernel_size=3, stride=1, padding=0不变，然后针对不同输入特征数(3-100)的数据进行卷积，独立重复50次实验取平均。我们涉及到的方法有：

朴素的一维卷积（baseline）；
广播优化（broadcast）；
使用SciPy的函数优化（scipy）；
im2col策略；
im2col+strided策略.

得到下面的特征数—计算时间对数图像：

test

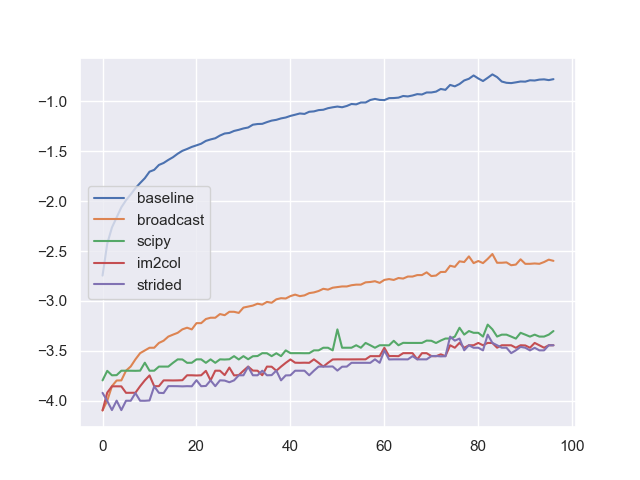
我们的最优实现，即im2col_strided策略能够比朴素实现快了将近1000倍。若具体考察我们本文提到的两种方法，同时与PyTorch中的一维卷积进行对比，则有下面的特征数—时间图像：

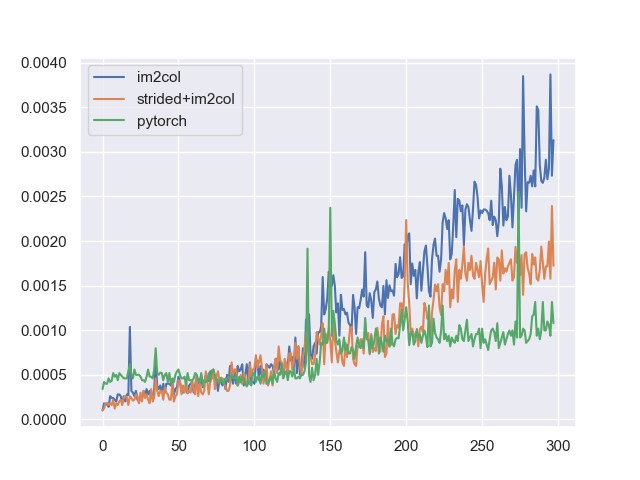
im2col

发现PyTorch中的一维卷积的一个特点是它的性能和输入特征数关系不大，我们的实现在一步步缩小与PyTorch的差距，从3:1缩减到了3:2。

Reference

Chellapilla, Kumar, Sidd Puri, and Patrice Simard. “High performance convolutional neural networks for document processing.” Tenth international workshop on frontiers in handwriting recognition. Suvisoft, 2006.
Harris, Charles R., et al. “Array programming with NumPy.” Nature 585.7825 (2020): 357-362.
How Are Convolutions Actually Performed Under the Hood?

基于im2col策略的卷积加速

一维卷积和二维卷积的朴素实现

一些不错的尝试

一维卷积的im2col

用NumPy自动构造矩阵

实验

Reference

CATALOG

FEATURED TAGS