前篇:《Understanding of a Convolutional Neural Network》的文献解读。
在CNN中,卷积运算是需要循环扫描数据实现的,难以向量化,从而拖慢的运行速度。本文是笔者在使用纯NumPy实现(卷积)神经网络中遇到该问题后,通过自己探索和阅读资料总结出的几种卷积操作加速方法。本文只考虑Conv1d,即一维卷积的前向传播过程。
一维卷积简介
在AI这边,最简单的一维卷积其实类似于数字信号处理中的计算相关,而不是卷积,设数据$\pmb x$长度为$m$,卷积核$\pmb a$的长度为$n$,那么CNN中的一维卷积:
\[\pmb x\star\pmb a=\bigg[\sum_{i=1}^{n}a_ix_i\quad\cdots\quad\sum_{i=m+1-n}^{m}a_ix_i\bigg]\]比如
\[\begin{bmatrix} x_1&x_2&x_3&x_4&x_5 \end{bmatrix}\star\begin{bmatrix} a_1&a_2&a_3 \end{bmatrix}=\begin{bmatrix} \sum_{i=1}^3a_ix_i&\sum_{i=2}^4a_ix_i&\sum_{i=3}^5a_ix_i \end{bmatrix}\]而在目前的深度学习及其框架中,一维卷积从以下三个方面进行了扩展:
- 卷积的方式:对数据进行padding,控制stride、dilation等;
- 引入了输入通道和输出通道的概念,输入通道类比图像的RBG三通道;输出通道数取决于有多少卷积核并行地卷积;
- 卷积需要针对批数据。
所以,送入一维卷积、以及一维卷积输出的数据,通常是三个维度:批数据大小、通道数、数据的特征数。比如PyTorch中的一维卷积:
import torch
from torch.nn import Conv1d
data = torch.randn(10, 2, 6) # 10条数据、数据为2通道、特征数为6
conv1d = Conv1d(
in_channels=2, # 需要和输入数据的通道数对其
out_channels=3, # 输出数据的通道数
kernel_size=3, # 卷积核大小
)
output = conv1d(data)
print(output.shape)
可以预测出一维卷积的结果应当是一个(10, 3, 4)的数据,实验结果也确实如此:
torch.Size([10, 3, 4])
Notation
为了后面表达的简便,我们声明一些量的简记:
- 输入数据的条数:$N$;
- 输入通道数:$C_\text{in}$;
- 输出通道数:$C_\text{out}$;
- 输入数据特征数:$F$;
- 卷积核长度:$K$.
- 填充0的数目(单边):$P$;
- 卷积核滑动步长:$S$。
最简单的Conv1d实现
我们考虑最简单的Conv1d实现,即完全基于for循环的实现。我们先仿照PyTorch,写出Conv1d类:
import numpy as np
class Conv1d:
'''
一维卷积
Parameters
----------
in_channels : 输入通道数;
out_channels : 输出通道数;
kernel_size : 卷积核长度;
stride : 卷积核移动步长,默认为1;
padding : 是否对数据进行0填充,以及填充的数量,默认不填充.
'''
def __init__(
self,
in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
) -> None:
self.in_channels = in_channels
self.out_channels = out_channels
self.kernel_size = kernel_size
self.stride = stride
self.padding = padding
self.kernel = np.random.randn(
self.out_channels,
self.in_channels,
self.kernel_size,
)
注意这里的卷积核,它是一个$N_\text{out}\times N_{\text{in}}\times K$的数组,self.kernel[i]就是第$i$个卷积核,它是一个$N_{\text{in}}\times K$的数组,self.kernel[i, j]就是第$i$个卷积核,针对第$j$个输入通道的卷积,它就是一个长度为$K$的数组,也就是我们在最前面提到的卷积核$\pmb a$。一个卷积核针对多个输入通道的卷积结果会被相加,所谓一个通道的输出。
我们考虑将上面的算法写出来,这里我们加入了padding和stride参数:
class Conv1d:
def baseline(self, x: np.array) -> np.array:
N, C_in, F = x.shape
C_out = self.out_channels
K = self.kernel_size
P = self.padding
S = self.stride
F_out = (F + 2 * P - K) // S + 1
output = np.zeros((N, C_out, F_out))
padding_x = np.pad(
x,
[(0, 0), (0, 0), (P, P)],
'constant',
) # 数据填充
# 卷积
for i in range(N):
for j in range(C_out):
for k in range(F_out):
for l in range(C_in):
for m in range(K):
output[i, j, k] += padding_x[i, l, k * S +
m] * self.kernel[j, l, m]
我们先用简单的数据进行测试:
x = np.arange(10).reshape(1, 1, 10) # 一条数据,一个输入通道,10特征
conv1d = Conv1d(1, 1, 3)
conv1d.kernel[...] = 1 # 人为设计卷积核
y = conv1d.baseline(x)
print(y)
结果
[[[ 3. 6. 9. 12. 15. 18. 21. 24.]]]
符合预期结果。我们再进行一个数组形状测试:
x = np.random.randn(100, 2, 12) # 100条数据,2个输入通道,12特征
conv1d = Conv1d(2, 1, 3, padding=1, stride=2) # 输出通道1,卷积核大小3
y = conv1d.baseline(x)
print(y.shape)
形状为
(100, 1, 6)
符合预期。
一维卷积的程序优化(1)
上面的程序,我们用了五重循环,这是一种及其耗时的操作。比如1000条数据,100个特征,三通道输入和三通道输出,卷积核长度为3的情况下,即使在服务器上跑也要2.2秒。因此我们考虑优化这个多重循环。
首先我们考虑卷积求和这一步骤,我们可以用NumPy广播替换掉for循环,举个简单的例子:
data = np.random.randn(100, 10)
kernel = np.random.randn(3)
output = np.zeros((100, 10 + 1 - 3))
for i in range(output.shape[1]): # 对特征列遍历
output[:, i] = np.sum(
output[:, i:i+3] * kernel,
axis=1,
)
我们利用NumPy广播机制,将对样本的遍历和对卷积核的遍历从Python中消除,而是交给了NumPy。而在多通道场景下,广播机制也能够将对输入通道的循环消除:
class Conv1d:
def calculate_shape(self, n_features):
return (n_features + 2 * self.padding -
self.kernel_size) // self.stride + 1
def broadcast_opt(self, x: np.array) -> np.array:
N, in_channels, n_features = x.shape
assert in_channels == self.in_channels
n_output = self.calculate_shape(n_features)
padding_x = np.pad(
x,
[(0, 0), (0, 0), (self.padding, self.padding)],
'constant',
)
output = np.zeros((N, self.out_channels, n_output))
for i in range(self.out_channels): # 对输出通道遍历
for j in range(n_output): # 对特征遍历
output[:, i, j] = np.sum(
padding_x[:, :, j * self.stride:j * self.stride +
self.kernel_size] * self.kernel[i, :],
axis=(1, 2),
)
return output
在这种优化下,对样本的遍历,对输入通道的遍历,对卷积核的遍历都交给了NumPy,使得影响这段程序性能的变量只有输入通道数和输出特征数。也就是说,数据量越大,输入通道越多的数据,该方法相比于baseline方法提升越大。
控制卷积核长度为3,输出通道为3,探究不同样本数,不同输入通道数以及不同输入特征下,两种方法的性能差距(独立重复10次实验取平均,对运行时间(秒)取对数):
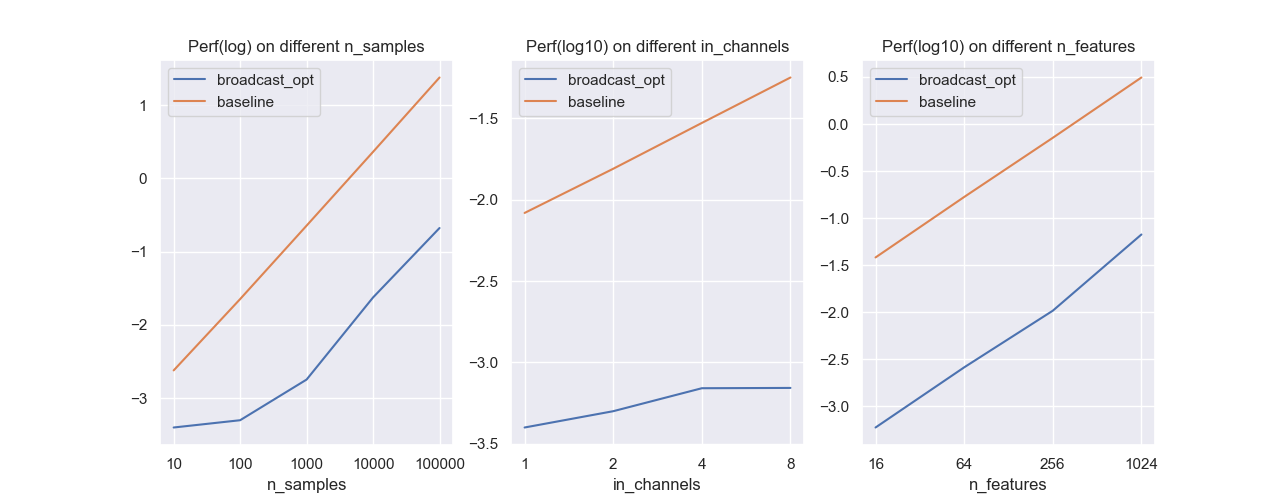
baseline的运行时间和这些变量是线性关系,由于我们的自变量是指数变化,而时间是取对数,所以可以发现baseline的图像是线性的。此外:
- 样本越多,广播优化相对于baseline的提升越大;
- 输入通道数越多,广播优化相对于baseline的提升越大;
- 输入特征越多,广播优化相对于baseline的提升会越来越小,但仍有至少百倍的优化。
一维卷积的程序优化(2)
广播优化在特征数大的情况下效果不好,原因就是我们仍是用Python循环去进行卷积。NumPy中有内置的convolve和correlate函数,但它们只支持单条一维数据卷积核相关运算。我们最终找到并选取了scipy模块中的correlate1d函数作为优化的卷积函数。下面的代码是一个corrlated简单的例子:
import numpy as np
from scipy.ndimage import correlate1d
x = np.array(
[
[1, 2, 3, 4],
[5, 6, 7, 8],
]
)
kernel = np.array([1, 2, 3])
output = correlate1d(x, kernel, origin=-1)[:, :4 + 1 - 3]
print(output)
输出
\[\begin{bmatrix} 14&20\\ 38&44 \end{bmatrix}\]scipy提供的一维卷积能够消除我们手动编写的样本循环,卷积循环和特征循环:
def scipy_corr_opt(self, x: np.array) -> np.array:
N, in_channels, n_features = x.shape
assert in_channels == self.in_channels
n_output = self.calculate_shape(n_features)
padding_x = np.pad(
x,
[(0, 0), (0, 0), (self.padding, self.padding)],
'constant',
)
output = np.zeros((N, self.out_channels, n_output))
for i in range(in_channels):
for j in range(self.out_channels):
output[:, j, :] += correlate1d(
padding_x[:, i, :],
self.kernel[j, i],
origin=-1,
)[..., :self.stride * n_output:self.stride]
return output
从上面的循环可以看出,当输入通道和输出通道数较多时,该方法的优势会越来越小。我们将其和前面的广播优化进行对比:
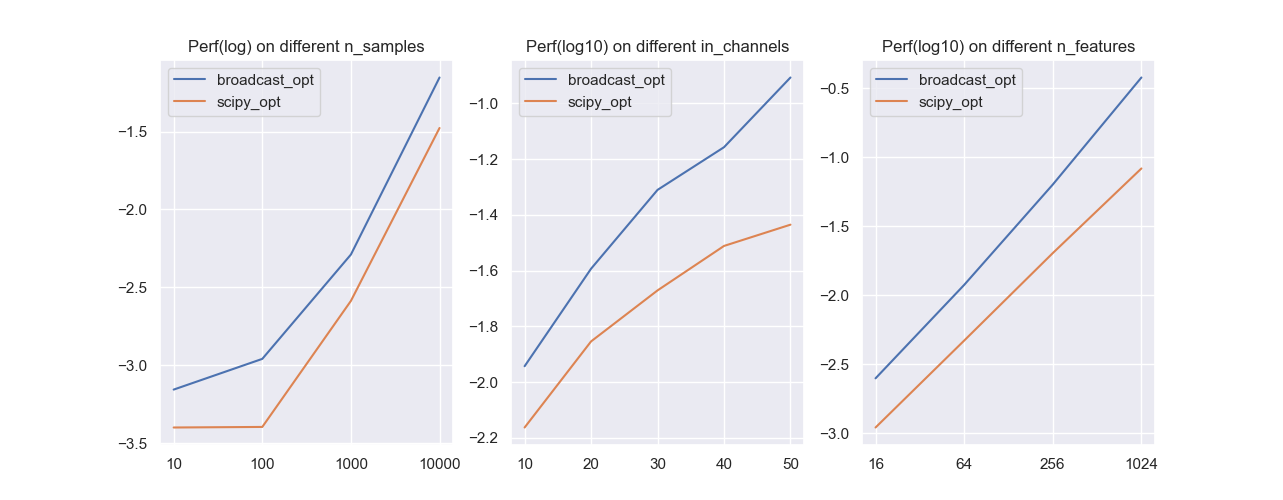
控制变量进行实验(仍是独立重复10次取时间的平均),可以发现通过scipy优化的一维卷积的计算速度更快,这是拜scipy内部高效的实现所赐。
和PyTorch的性能对比
我们将自设计的方法和PyTorch中的一维卷积进行对比,同样是针对样本数,输入通道数和输入特征数这几个变量进行实验:
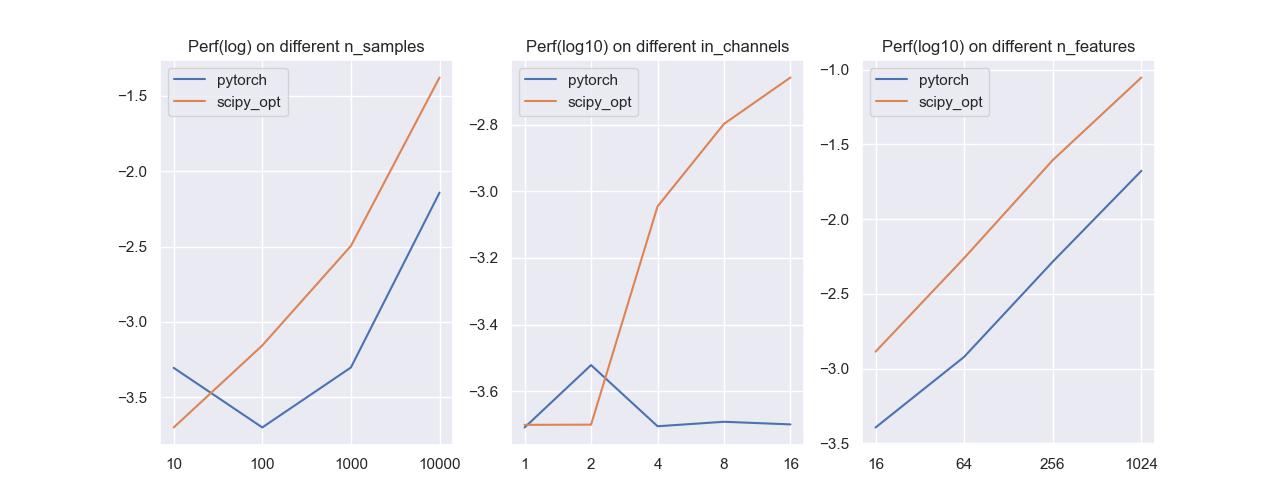
可以发现我们的实现和PyTorch还是有差距的,但在样本量和通道数都不大的时候,我们的方法会稍微占优。