笔者在很久之前写过一篇《计算图与自动微分》,介绍了当今流行的深度学习框架,比如Pytorch,TensorFlow的基础原理:计算图与自动微分。基于这样机制,框架能够简单,快捷地计算目标函数梯度以进行梯度下降。当时有实现它的打算,但由于能力原因(更多是不敢去想)拖延了。
论文《Automatic differentiation in machine learning: a survey》是对自动微分和机器学习的一个综述,它总结对比了现有的微分方法,介绍自动微分的算法和发展历程,以及其在机器学习领域的应用。
笔者近期重拾过去的想法,实现一个可自动微分的计算图,并在此基础上构建了神经网络。因此后面几篇文章都是关于这部分理论和实现的日志(水文章)。今天我们主要是从计算图和自动微分的机制说起,这是对之前那篇文章的补充和拓展。
注:为了简洁,我们会将自动微分简写为AD。
AD为什么好
这个标题等价于问:为什么其他的求导方法不好。首先我们得知道目前计算机程序求导的四种方法:
- 手动求导,然后将导数编写进程序里;
- 基于差分近似的数值微分;
- 通过表达式的代数推导得到导数的表达式,这种方法的代表:Mathmatica,Maxima和Maple;
- 自动微分。
前三种求导方法存在不同的劣势:手动求导工作量大且易出错(不准且效率低);数值微分受到截断误差和舍入误差的干扰,影响精度,且如何选择差分步长是没有定论的(不准);而表达式求导更在乎的是明晰的导数表达式,而我们在机器学习领域更在意的是导数的值,且不论不少情况下导数是没有准确的解析形式(closed-form),求导常常会让表达式的规模几何级增加,造成表达式膨胀(效率低)。
“AD通过替换变量的域来包含导数值,并重新定义算子的语义,使算子的语义来解释给定的计算机程序的传播导数。”(原文)
AD是什么
AD中的“自动”一词可能是混淆的来源,导致机器学习从业者将“Auto Differentiation”甚至是“autodiff”的标签放在任何不涉及手动求导的方法或工具上,而没有对潜在机制给予适当的关注。我们想强调的是,AD作为一个技术术语指的是一系列特定的技术,它通过在代码执行过程中积累值来计算导数来生成数值导数计算,而不是导数表达式。
自动微分不属于数值微分和符号微分中的任意一种。论文中一张图展示了它们的区别:
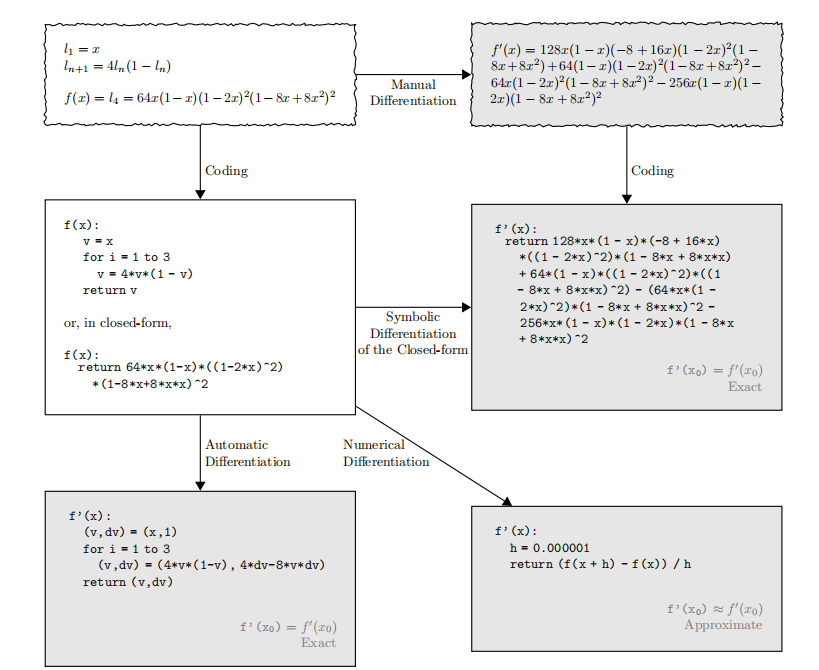
自动微分兼具符号微分的精确和数值微分的简洁,避免的两种方法的缺陷。
AD的两种模式
计算图的两个功能是求值和求导,求导分为前向模式和后向模式,分别针对不同的情景。我们先来看求值,对于下面的计算图
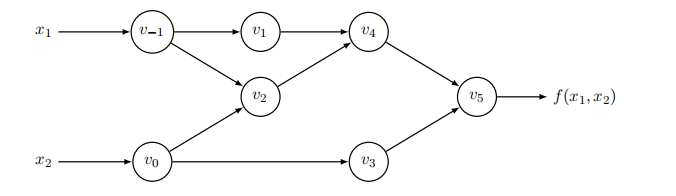
它描述了一个二元函数$f(x_1,x_2)=\ln(x_1)+x_1x_2-\sin(x_2)$。每个节点都是一个运算,入度为2的表示一个二元运算,比如加减乘除;入度为1则是一元运算,比如取负,三角函数,$\exp$,$\log$等。
注意到合法的计算图是有向无环图,且对于任意的节点,它执行计算的必要条件是其上游所有节点都已经计算完毕,可以看出这是一个拓扑排序过程。实际上,我们也可以不需要想得这么复杂,因为程序在计算表达式时都是要知道其操作数的值再计算的。
前向模式
前向累积模式(Forward accumulation mode)是概念上最简单的模式,也就是求导和求值是同向的。考虑上面的计算图,假如我们要求$f$对$x_1$的导数,那么从$v_{-1}$开始,先计算$\partial v_{-1}/\partial x_1$;然后计算$\partial v_{1}/\partial v_{-1}$和$\partial v_{2}/\partial v_{-1}$,利用链式法则,即导数相乘,得到$\partial v_{1}/\partial x_{1}$和$\partial v_{2}/\partial x_{1}$……按照这样的顺序,我们终究可以得到$\partial f/\partial x_1$的导数的数值。
一个有趣的事情是,由于笔者是先学神经网络的反向传播后学自动微分,所以默认了反向求导,而忽视了正向求导的存在性和合理性。
拓展到多元函数$f:\mathbb{R}^n\to\mathbb{R}^m$,如果要求$f_i$对$x_j$的偏导,即Jacobi矩阵的第$i$行第$j$列,我们将搜索从$x_j$节点到$f_i$节点的所有的路径,如果几条路径有合并,说明合并点是一个二(多)元运算符,应该按照对应的求导规合并分支,比如加法节点是将输入梯度进行相加;如果发生路径分叉,当然,我们也可以不限制$f_i$,只考虑$x_j$及其可达节点的子图(比如在上图中,$v_0$和$v_3$就是$v_{-1}$不可达的节点),然后以拓扑序进行前向模式,这样就能获得$\partial\pmb f/\partial x_j$,即Jacobi矩阵的第$j$列。
对于$n\gg m$的情况,也就是输入远大于输出时,前向模式不再适用,因为我们要进行$n$次前向模式求导才能获得Jacobi矩阵。而在机器学习领域,比如神经网络,其输入为多个网络参数,输出只有一个损失函数,因此前向模式无法高效利用于该领域。
反向模式
反向累积模式(Reverse accumulation mode)对应反向传播算法的广义形式,或者说,反向传播是反向模式的特例,因为反向传播针对的是输入为多变量,输出为单变量(更严格的说,是标量,即损失函数项)的函数,但AD针对的是广义的多元函数。
注:论文中有提到,实际上反向传播和自动微分在一段时期分别由AI领域和计算数学领域独立提出,两个方向直到近期深度学习的大步发展才有所联通。
如果读者有反向传播基础的话会更容易读懂这部分。我们再次考虑函数
\[f(x_1,x_2)=\ln(x_1)+x_1x_2-\sin(x_2)\]现在要求出$f$对$x_1$的导数,那么
\[\begin{aligned} \dfrac{\partial f}{\partial x_1}&=\dfrac{\partial}{\partial x_1}(\ln(x_1)+x_1x_2)-\dfrac{\partial}{\partial x_1}\sin(x_2)\\ &=\dfrac{\partial}{\partial x_1}\ln(x_1)+\dfrac{\partial}{\partial x_1}x_1x_2-\dfrac{\partial}{\partial x_1}\sin(x_2)\\ &=\dfrac1{x_1}+x_2 \end{aligned}\]从我们手动求导的例子中可以发现,求导方向是从计算图末端向前段流动。如果采用计算图节点的写法,求导过程实际上用到了链式法则。如果我们将减法视作一个二元函数$\text{sub}(x,y)=x-y$,那么$v_5=\text{sub}(v_4,v_3)$,那么
\[\dfrac{\partial v_5}{\partial x_1}=\dfrac{\partial\text{sub}(v_4,v_3)}{\partial v_4}\dfrac{\partial v_4}{\partial v_1}+\dfrac{\partial\text{sub}(v_4,v_3)}{\partial v_3}\dfrac{\partial v_3}{\partial v_1}\]求得$\text{sub}$对两输入变量的导数后,接着使用类似的方法计算$\partial v_4/\partial v_1$和$\partial v_3/\partial v_1$,也就是说,梯度按照计算图反向流动,一直流动到$x_1$。如果流动路径有分叉(对应计算图的合并),说明经过多元运算符,那么此时的梯度将经过不同的处理流入不同的直流,比如减法节点,梯度需要乘以-1才能进入减数对应的分叉,而被减数对应的分叉流入的是原样的梯度(因为只需要乘以1)。如果路径有合并(对应计算图的分叉),此时的梯度应当是流入该节点的梯度之和。这也暗示了反向传播需要按照拓扑序进行,但这里是逆拓扑排序,即将计算图中所有的有向边反向(反向图)后进行拓扑排序。
同样的,拓展到多元函数$f:\mathbb{R}^n\to\mathbb{R}^m$,如果要求$f_i$对$x_j$的偏导,即Jacobi矩阵的第$i$行第$j$列,我们同样搜索所有$x_j$节点到$f_i$节点的路径进行反向模式。当然,我们也可以不限制$x_j$,只考虑计算图的反向图中$f_i$及其所有可达节点构成的子图进行反向模式,这样就可以求得$\partial f_i/\partial\pmb x$,即Jacobi矩阵的一行。
两种模式的比较
对多元函数$f:\mathbb{R}^n\to\mathbb{R}^m$求导,实际上就是求Jacobi矩阵,它是$m\times n$的。前向模式一次能获得Jacobi矩阵的一列,所以需要$n$次前向模式才能得到整个Jacobi矩阵。类似的,通过$m$次后向传播才能等得到Jacobi矩阵。对于同一个计算图,前向模式和后向模式都需要进行一个拓扑排序,所以时间上差别不大。所以,对于输入多,输出少的计算图,比如神经网络,后向模式效率更高,否则我们应该用前向模式。
笔者想起之前做过的作业题:为什么神经网络求梯度是反向传播而不是前向传播?笔者当时的回答是:因为反向传播时,我们能够用到上一层求导的结果,这样避免了重复计算。现在看来我的回答是不对的,”用到上一层求导的结果“的特性来源于链式法则,而前向传播(即前向模式)也能用到。正确的答案应当是我们上面的论述。
总结
我们在这里对计算图和自动微分机制进行了细致的介绍,基于上面的知识,我们能够实现一个计算图,辅以自动微分机制。我们在后面会解读实现过程和细节。