在NLP等易发生维数爆炸(curse of dimensionality)的情景下,对数据降维则成为一个重要的环节。在《Text Classifification Algorithms: A Survey》中,作者提及了面对文本分类维数过大的情况下,常用的降维方法。这些降维方法显然能用于其余任务,具有普适性,故笔者在这里进行整理。
成分分析
成分分析分为主成分分析 (PCA)和独立成分分析 (ICA)。
主成分分析
主成分分析尝试找到数据集中的主成分 (实际上就是一个向量组),然后用这些主成分重新描述数据。我们希望在这些主成分的重构下,数据能够用”最大可分性”和”最近重构性”。在https://welts.xyz/2021/05/22/pca/中,我们对PCA算法做出了详细的推导。
除了对数据降维,PCA还可以实现降噪,从而缓解过拟合问题。核PCA (KPCA)将核方法融入PCA,实现了非线性降维。
独立成分分析
独立成分分析一开始用于解决盲信号分离问题。最经典的案例就是“鸡尾酒会问题”:在一场$n$人参加的鸡尾酒会会场中 放置$n$个录音设备,我们希望通过这$m$个录音设备中的混合人声中提取出$n$人各自的声音。
独立成分分析假定存在一个线性变换将$n$种人声进行混合:
\[\begin{bmatrix} x_1(t)\\ x_2(t)\\ \vdots\\ x_n(t)\\ \end{bmatrix}=A_{n\times n}\begin{bmatrix} s_1(t)\\ s_2(t)\\ \vdots\\ s_n(t)\\ \end{bmatrix}\]其中$\pmb s$是原信号,$\pmb x$是分类出来的信号,同时称$A$为混合矩阵。我们尝试在已知$\pmb x$的情况下,推出$A$和$\pmb s$。具体的算法可以参考这里.
原文并没有说明如何使用ICA进行降维,上面的应用显然只是对复合信号的分解。笔者认为一种可能的降维方式,就是类似PCA,以某种标准选取$A$的某些行作为$A$的替代,从而实现降维。
PCA和ICA的一个根本的不同点在于,PCA假设源信号间彼此不相关,ICA假设源信号间彼此独立。
线性判别分析
线性判别分析(LDA)属于有监督的降维,它的目标是降维之后,同类样本尽可能的近,异类样本尽可能远。
以二分类问题为例,同类样本尽可能近,等价于让两类样本在投影后的协方差矩阵尽可能小:
\[\begin{aligned} \min_{\pmb w}\quad f_1(\pmb w)&=\pmb w^T\Sigma_0\pmb w+\pmb w^T\Sigma_1\pmb w\\ &=\pmb w^T(\Sigma_0+\Sigma_1)\pmb w\\ &=\pmb w^T(\sum_{i:y_i=0}(\pmb x_i-\pmb\mu_0)(\pmb x_i-\pmb\mu_0)^T+\sum_{i:y_i=1}(\pmb x_i-\pmb\mu_1)(\pmb x_i-\pmb\mu_1)^T)\pmb w \end{aligned}\]其中$\pmb\mu_0$和$\pmb\mu_1$表示两类样本的中心。考虑LDA的目标之二:异类样本尽可能远,即两样本的中心在投影后尽可能远,即
\[\max_{\pmb w}\quad f_2(\pmb w)=\Vert{\pmb w^T\pmb\mu_0-\pmb w^T\pmb\mu_1}\Vert_2^2\]因此将两目标综合,我们实际上求解的是优化问题
\[\max_{\pmb w}\quad\dfrac{f_2(\pmb w)}{f_1(\pmb w)}=\dfrac{\pmb w^T(\pmb\mu_0-\pmb\mu_1)(\pmb\mu_0-\pmb\mu_1)^T\pmb w}{\pmb w^T(\Sigma_0+\Sigma_1)\pmb w}\]是广义瑞利商的形式,利用拉格朗日对偶函数可以求解,这里不作赘述。总之,在求出$\pmb w$后,就可以将$n$维数据投影到一个$n$维超平面上,等价于$n-1$维。
非负矩阵分解
非负矩阵分解(NMF)尝试将将一个非负矩阵$V_{n\times m}$分解成两个非负矩阵$W$和$H$:
\[V_{n\times m}\approx W_{n\times r}H_{r\times m}\]如果
\[mn<nr+rm\to r\leq\dfrac{mn}{m+n}\]那么此时$W$和$H$可视作矩阵$V$的降维。显然我们的目标是让$WH$尽可能逼近$V$,即
\[\min_{W,H}\quad\frac12\Vert{V-WH}\Vert_F\\ \text{s.t.}\quad W\succeq0,H\succeq0.\]其中$\Vert\Vert_F$是矩阵的Frobenius范数。该问题的双变量,有约束的凸优化问题。一个朴素的想法是交替进行投影梯度下降。
当然,衡量矩阵间的差异不只有Frobenius范数,其他的度量,比如KL-散度导出了不同的NMF方法。
NLP的词袋模型,N-gram模型,以及延伸出来的TF-IDF,虽然让数据高度稀疏化,但保证数据集矩阵的非负性。因此NMF很好契合了这些模型的特点。对于单词-文档矩阵,使用NMF进行分解,能够同时得到单词向量和文档向量的稀疏表示。
随机投影
随机投影是一种新的降维技术,主要用于高容量数据集或高维特征空间。文本和文档,特别是通过加权特征提取,会产生大量的特征。许多研究人员已经将随机投影应用于文本数据中进行文本挖掘、文本分类和降维。
随机傅里叶特征
随机傅里叶特征 (RFF)主要是针对的是核函数 (移位不变核)的降维。核函数会将数据映射到甚高维,但随机傅里叶特征通过蒙特卡洛抽样将数据从甚高维降到相对的低维。
随机傅里叶特征的推导需要概率统计和数字信号处理的知识,可参见笔者的https://welts.xyz/2021/10/30/fourier_kernel/。这里列出核心公式:
\[\begin{aligned} k(\pmb x-\pmb y)&=\int_{\mathbb{R}^d}p(\pmb w)e^{j\pmb w^T(\pmb x-\pmb y)}\mathrm d\pmb w\\ &=\textbf{E}_{\pmb w}[e^{j\pmb w^T(\pmb x-\pmb y)}]\\ &=\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y))]\\ &=\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y)+2b)]+\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y))]\\ &=\textbf{E}_{\pmb w}[\sqrt 2\cos(\pmb w^T\pmb x+b)\sqrt 2\cos(\pmb w^T\pmb y+b)]\\ &=\textbf{E}_{\pmb w}[z_{\pmb w}(\pmb x) z_{\pmb w}(\pmb y)]\\ &=\dfrac1D\sum_{m=1}^Dz_{\pmb w_m}(\pmb x)z_{\pmb w_m}(\pmb y)\\ &=z(\pmb x)^Tz(\pmb y) \end{aligned}\]Johnson Lindenstrauss Lemma
William B. Johnson和Joram Lindenstrauss证明了对任何给定的$\epsilon\in(0,1)$和$N$维欧几里得空间中的任意$m$个点,对于任意满足下式的$n$
\[n>(\frac{\epsilon^2}{2}-\frac{\epsilon^3}{3})^{-1}\log m\]存在一个线性映射$f:R^N\to R^n$,能够将这$m$个点投影到$n$维的低维空间中。同时基本保持了点与点之间的相对距离(保距映射)。
即$\forall i,j\in[1,m],i\neq j$,总有
\[(1-\epsilon)\Vert{x_i-x_j\Vert}_2^2\leq\Vert{f(x_i)-f(x_j)}\Vert_2^2\leq(1+\epsilon)\Vert{x_i-x_j}\Vert_2^2\]Autoencoder
自编码器是一种神经网络,它被训练去试图将其输入复制到其输出,自编码器作为一种降维方法取得了巨大的成功。Autoencoder的雏形是一个单隐层的神经网络,我们想将这个神经网络训练成一个单位映射,也就是输入和输出相同。如果我们将单隐层神经元数目设置成比输入要小,则可以将其隐层的数据作为输入数据的降维表示。
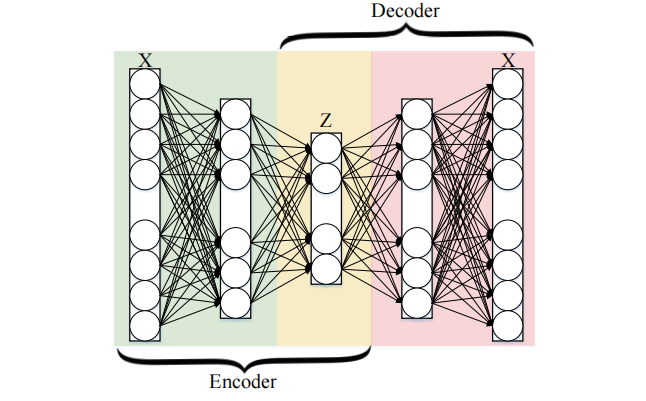
如图所示,一个一般的Autoencoder包括一个编码器(Encoder)和解码器(Decoder),分别将数据进行降维和还原。
卷积自编码器将卷积神经网络思想融入了自编码器。也就是数据输入后,经过卷积,池化后形成了低维向量,这是编码器部分。然后通过反池化和反卷积操作,将降维后的数据进行还原,这是解码器部分。事实上卷积自编码器在处理图像降噪上有不小的贡献。
循环自编码器则是借用了循环神经网络的结构,如图所示:
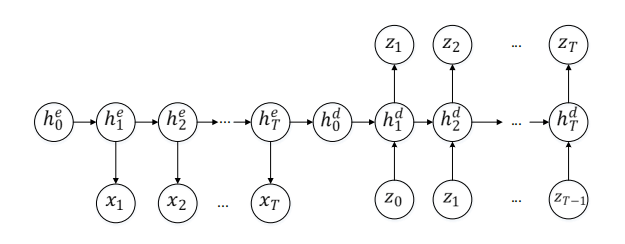
我们知道,循环神经网络在每一层 (时刻)计算的是上一时刻传入和状态向量和这一时刻的输入的共同作用。以$\tanh$作为激活函数,则有
\[\begin{aligned} h_t&=\tanh(W_1 x_t+W_2h_{t-1})\\ y_t&=W_3h_t \end{aligned}\]$x$是一个序列输入$(x_1,\cdots,x_T)$,$y$对应输出$(y_1,\cdots,y_T)$。一个多项式分布能够用一个softmax激活函数输出(原文如此)
\[p(x_{t,j}=1\vert x_{t-1,\cdots,1})= \dfrac{\exp(w_jh_t)} {\sum_{j'=1}^K\exp(w_{j'}h_t)}\]从而得到序列$x$的概率
\[p(x)=\prod_{t=1}^Tp(x_t\vert x_{t-1},\cdots,x_1)\]t-SNE
t-SNE (T-distributed Stochastic Neighbor Embedding)是一种非线性降维方法,特别适用于高维数据集的可视化。该方法将高维的欧几里得距离转换成表征相似度的条件概率:
\[p_{j|i}=\dfrac{\exp(-\frac{\Vert{x_i-x_j}\Vert_2^2}{2\sigma_i^2})}{\sum_{k\neq i}\exp(-\frac{\Vert{x_i-x_k}\Vert_2^2}{2\sigma_i^2})}\]其中$\sigma_i$是以$x_i$为中心的方差。$y_i$和$y_j$,即降维后数据间的相似性:
\[q_{j|i}=\dfrac{\exp(-\Vert{y_i-y_j}\Vert_2^2)}{\sum_{k\neq i}\exp(-\Vert{y_i-y_k}\Vert_2^2)}\]将两分布的KL散度作为损失函数,KL散度越小,说明分布越相似,降维效果越好:
\[C=\sum_iKL(P_i\Vert Q_i)=\sum_{i}\sum_{j}p_{j|i}\log\dfrac{p_{j|i}}{q_{j|i}}\]然后用梯度下降法求解。
总结
本文介绍了几种常用的降维算法,但都是浅尝辄止,读者若有兴趣可深入了解,后续笔者可能会挑选一些方法进行重点探讨。