原文地址: https://link.springer.com/content/pdf/10.1007/s10994-010-5221-8.pdf.
引入
给定二分类数据集$\{\pmb x_i,y_i\}_{i=1}^l$,$\pmb x_i\in\mathbb{R}^n$,$\pmb y_i\in\{-1,+1\}$,$i=1,\cdots,l$,考虑对率回归问题(Logistic Regression, LR)
\[\min_{\pmb w,b}\quad \sum_{i=1}^l\log(1+e^{-y_i(\pmb w^T\pmb x_i+b)})\]通过对数据增广,同时加上正则化项,我们得到L2正则的对率回归问题
\[\min_{\pmb w}\quad \frac12\pmb w^T\pmb w+C\sum_{i=1}^l\log(1+e^{-y_i\pmb w^T\pmb x_i})\]对应的对偶问题为
\[\begin{aligned} \min_{\pmb\alpha}&\quad \frac12\pmb\alpha^TQ\pmb\alpha+\sum_{i:\alpha_i>0}\alpha_i\log\alpha_i+\sum_{i:\alpha_i<C}(C-\alpha_i)\log(C-\alpha_i)\\ \text{s.t.}&\quad0\leq\alpha_i\leq C,i=1,\cdots,l \end{aligned}\]其中$Q_{ij}=y_iy_j\pmb x_i^T\pmb x_j$。如果考虑到$0\log0=0$,那么上式可简化为
\[\begin{aligned} \min_{\pmb\alpha}&\quad \frac12\pmb\alpha^TQ\pmb\alpha+\sum_{i=1}^l\alpha_i\log\alpha_i+(C-\alpha_i)\log(C-\alpha_i)\\ \text{s.t.}&\quad0\leq\alpha_i\leq C,i=1,\cdots,l \end{aligned}\]这篇论文考虑用坐标下降法求解对率回归的对偶问题,尽管大部分算法是针对原问题提出的。这里设计的坐标下降法不仅能够解决对率回归数值计算上的问题(因为有对数运算),同时在性能上超过了当时大部分训练对率回归分类器的算法。
坐标下降方法
针对带等式约束和不等式约束的优化问题
\[\begin{aligned} \min_{\pmb\alpha\in\mathbb{R}^l}\quad& F(\pmb\alpha)\\ \text{s.t.}\quad& A\pmb\alpha=\pmb b,\pmb 0\leq\pmb\alpha\leq C\pmb e \end{aligned}\]那么坐标下降问题在选定分量上求解的是子问题
\[\begin{aligned} \min_{\pmb z}\quad& F(\pmb\alpha+\pmb z)\\ \text{s.t.}\quad& z_i=0,\forall i\notin B,\\ &A\pmb z=\pmb0,0\leq\alpha_i\leq z_i\leq C,\forall i\in B \end{aligned}\]其中$B\subset\{1,\cdots,l\}$是坐标子集,表示子问题考虑的坐标集合。我们下面举出坐标下降的三个例子,分别是
- 精确求解SVM对偶问题的单变量子问题;
- 近似求解LR原问题的单变量子问题;
- 未增广SVM对偶问题的多变量子问题.
对于SVM对偶问题,坐标下降子问题为
\[\begin{aligned} \min_{z}\quad&\frac12Q_{ii}z^2+\nabla_iD^{\text{SVM}}(\pmb\alpha)z+\text{constant}\\ \text{s.t.}\quad&0\leq\alpha_i+z\leq C \end{aligned}\]详细推导可见https://welts.xyz/2021/12/02/dcdm/. 显然我们可以得到更新单变量的闭式解:
\[z=\min(\max(\alpha_i-\frac{\nabla_iD^{\text{SVM}}(\pmb\alpha)}{Q_{ii}},0),C)-\alpha_i\]而对于LR原问题,对第$j$个分量进行坐标下降法求解的是最小化
\[g(z)=\frac{z^2}2+zw_j+C\bigg(\sum_{i=1}^l\log(1+\frac{e^{zx_{ij}}-1}{1+e^{-y_i\pmb w^T\pmb x_i}})-z\sum_{i=1,y_i=1}^lx_{ij}\bigg)+\text{constant}\]这时我们无法像上面那样求出闭式解,因此需要采用迭代求解方法,比如牛顿法:
\[z\gets z-\frac{g'(z)}{g''(z)}\]LR问题的目标函数是二阶连续的,因此求上式的一阶导数和二阶导数是可行的,但计算代价昂贵,需要进一步优化。
考虑没有进行数据增广下的SVM对偶问题:
\[\begin{aligned} \min_{\pmb\alpha}&\quad\frac12\pmb\alpha^TQ\pmb\alpha-\sum_{i=1}^l\alpha_i\\ \text{s.t.}&\quad\sum_{i=1}^ly_i\alpha_i=0,0\leq\alpha_i\leq C,\forall i. \end{aligned}\]由于此处有等式约束,因此子问题求解至少需要2个变量,比如SMO算法就是一次对两个变量进行更新。
针对LR问题的对偶坐标下降
尽管LR对偶问题和SVM对偶问题相似,但存在很大区别。其中一点就是,SVM的对偶坐标下降通常会将初始解$\pmb\alpha$设置为$\pmb0$,这是为了保证解的稀疏性。但对于LR问题,它在$\alpha_i=0$或$C$的时候不是良定义(not well defined)的,这就导致初始解$\pmb\alpha$必须在开区间$(0,C)^l$。甚至说,我们不能确定最优解是否出现$\alpha_i=0$或$C$。本文作者证明了下面的定理:
定理1:LR对偶问题有一个全局最优解$\pmb\alpha^*$且$\pmb\alpha\in(0,C)^l$。
此外,SVM对偶问题的坐标下降子问题是有解析解的,但LR对偶问题的子问题是求解
\[\begin{aligned} \min_z\quad& g(z)=(c_1+z)\log(c_1+z)+(c_2-z)\log(c_2-z)+\frac a2z^2+bz\\ \text{s.t.}\quad&-c_1\leq z\leq c_2 \end{aligned}\]其中$c_1=\alpha_i,c_2=C-\alpha_i,a=Q_{ii},b=(Q\pmb\alpha)_i$。显然该问题是没有闭式解的,因此采取牛顿法求解:
\[z^{k+1}\gets z^k+d,d=-\frac{g'(z^k)}{g''(z^k)}\]对于$(-c_1,c_2)$内的$z$,可以求得$g(z)$的一阶和二阶导数:
\[\begin{aligned} g'(z)&=az+b+\log\frac{c_1+z}{c_2-z}\\ g''(z)&=a+\frac{c_1+c_2}{(c_1+z)(c_2-z)} \end{aligned}\]为了确保收敛性,我们通常采用线搜索去找一个确保收敛的牛顿步径,即找到第一个满足下面条件的$\lambda=1,\beta,\beta^2,\cdots$:
\[g(z^k+\lambda d)-g(z)\leq\gamma\lambda g'(z^k)d\]其中$\gamma,\beta\in(0,1)$。在迭代中维护解向量已经是常规操作了:
\[\pmb w=\sum_{i=1}^ly_i\alpha_i\pmb x_i\]通过下式更新解向量
\[\pmb w(\pmb\alpha+z\pmb e_i)=\pmb w(\pmb\alpha)+zy_i\pmb x_i\]通过这样的设置,我们可以很快计算$(Q\pmb\alpha)_i$:
\[(Q\pmb\alpha)_i=y_i\pmb w^T\pmb x_i\]在每一轮坐标下降更新中,我们需要做的事情:
- 构建子问题,尤其是$(Q\pmb\alpha)_i$,从上面可以知道时间是$O(n)$;
- 寻找牛顿方向$d$,涉及到对数运算,时间是$O(1)$;
- 在线搜索过程中计算$g(z^k+\lambda d)$,时间是$O(1)$.
在通常情况下,先搜索一次就可以找到适合的牛顿步径。虽然第二步的公式很简单,但其中的对数运算耗时远超普通加减法;此外,线搜索过程中频繁使用$\log$运算也使得线搜索代价远超第2步,尽管两者的时间复杂度相同。因此,论文在下面提出改进的坐标下降法。
改进的子问题求解法
我们期望在新算法不需要线搜索的场景下也可以保持收敛性。作者这里证明了下面的定理:
定理2:LR对偶问题的子问题有一个全局最小值点$z^\ast$,且$z^\ast*\in(-c_1,c_2),g’(z^\ast)=0$。
下图展示了牛顿法求根(也就是求导函数的零点)的两种情况:
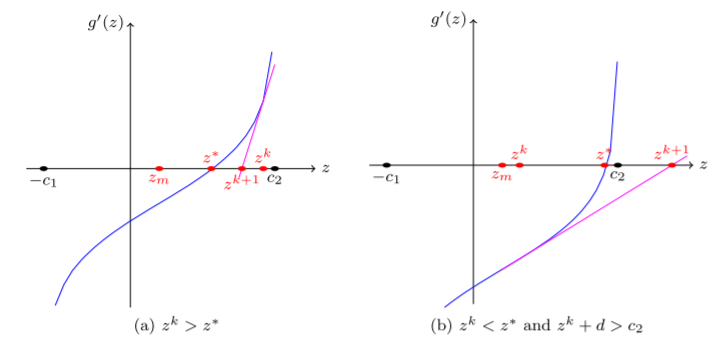
其中$z^k$是初始点,$z^{k+1}$是由牛顿步径导出的位置,$z^*$是最优值点,而$z_m=(c_2-c_1)/2$,也就是可行区间的中点。图(a)展示了一个好的初始点能让牛顿法奏效;图(b)则是一种糟糕的情形:牛顿迭代让$z^{k+1}$跳至区间外。
因此我们需要一种机制,让所有的点都能到达正确的一边,也就是图(a)所示。从上图可以发现(理论上也是),$g’(z)$在$(-c_1,c_m]$上为凹函数,在$[c_m,c_2)$上是凸的。于是作者提出下面的定理判断$z^k$是否在正确的一边:
定理3: 如果$z^\ast\geq z_m$,那么由牛顿法生成的${z^k}$会收敛到$z^\ast$只要初始点在$[z^\ast,c_2)$上;如果$z^\ast\leq z_m$,那么$\{z_k\}$会收敛到$z^\ast$只要初始点在$(-c_1,z^\ast)$。
对于上述两条件之一的$z^k$,我们称它在$z^*$正确的一边。如果上述条件皆不满足,则又分以下几种情况:
- $z^{k}+d$没有越界,且处于正确的一边: 满足条件,令$z^{k+1}=z^k+d$继续迭代即可;
- $z^{k}+d$没有越界,但处于错误的一边: 考虑它离最优解更近,令$z^{k+1}=z^k+d$,继续迭代;
-
$z^{k}+d$越界,由于合法区间是开区间,无法做投影。不失一般性,设$z^{k+1}+d\geq c_2$。我们希望找到点$z\in[z^k,c_2)$更接近于正确的一边:
\[z^{k+1}=\xi z^k+(1-\xi)c_2,\xi\in(0,1)\]因为$z^k$处于错误的一边,作者证明了上述设置最终可以让点到达正确一边,然后这个点就作为满足定理3的起始点进行迭代。
定理4: 假定$z^\ast\geq z_m$,如果我们以$z^k<z^\ast$为起始点生成牛顿迭代序列(也就是从错误一边开始),同时用下面的更新规则:
\[z^{k+1}=\begin{cases} z^k+d&\text{if }z^k+d<c_2\\ \xi z^k+(1-\xi)c_2&\text{if }z^k+1\geq c_2 \end{cases}\]从而会有一个$k’>k$使得$z^{k’}\geq z^\ast$,也就是说,$z^{k’}$是在正确的一边。对于$z^\ast\leq z_m$且$z^k>z_m$的情况是相似的。
基于上述定理,作者提出下面的算法用于求解LR对偶问题子问题:

可以发现该算法摆脱了线搜索,基于定理3和定理4,该算法的收敛性显然成立,有下面的定理:
定理5: 由上述算法生成的$\{z_k\}$可收敛到$z^*$,这对任意$z^0\in(-c_1,c_2)$都成立。
虽然定理5声明了初始点的随意性,但我们仍希望有更快的收敛速度,因此初始点的选择还是重要的。在整个坐标下降算法的后期,显然$\alpha_i$变化越来越小,相应的,$z^*\approx0$,将初始点设成0是有道理的。但显然在算法前期这样的设置是不合理的。此外,由于最优点未知,我们无法将初始点指定在正确的一边。定理3希望我们这样设置初始点:
\[z^0\in\begin{cases} (-c_1,z_m),&\text{if }z^*\leq z_m,\\ [z_m, c_2),&\text{if }z^*\geq z_m. \end{cases}\]因此作者选用了总体为0,但稍有调整的初始化方案:
\[z^0=\begin{cases} (1-\xi_0)(-c_1)&\text{if }z^*\leq z_m\leq0\\ (1-\xi_o)c(c_2)&\text{if }z^*\geq z_m\geq0\\ 0&\text{else} \end{cases}\]我们设置$0<\xi_0\leq0.5$,这样可以让$z^0$满足定理3所希望的初始化方式:若
\[-c_1<z^*\leq z_m\leq 0<c_2\]那么$(1-\xi_0)(-c_1)\in(-c_1,0)$而且离$-c_1$更近,也就是满足$(1-\xi_0)(-c_1)\leq z_m$。$z^*\geq z_m\geq 0$的情况与之类似。
数值计算上的困难
不幸的是,作者发现上面提出的改进坐标下降法在数值计算上存在阻碍。具体来说,就是当$\alpha_i$接近0或$C$时,算法很难去到达最优点$z^*$,也就是导数为0:
\[g'(z^*)=Q_{ii}z^*+(Q\pmb\alpha)_i+\log(\alpha_i+z^*)-\log(C-\alpha_i-z^*)\approx0\]2005年的一篇论文指出,当$C$很大(比如$10^5$)时,$(Q\pmb\alpha)_i$也很大,那么$\alpha_i+z^*$就可能会很小(比如$10^{-5}$),在浮点数表示上有困难。但作者通过实验发现,即使$C$有这么大,$(Q\pmb\alpha)_i$也没有很大,通常也就几百几千的样子。作者发现数值计算问题出现在巨量消失(catastrophic cancellations,也就是两个相近数值的减法),即$\alpha_i+z$接近于0的时候。此时计算$\log(\alpha_i+z)$会将错误进一步扩大。
一种解决方案是将问题重构,令$Z_1=c_1+z$,$s=c_1+c_2$,因此得到子问题的等价形式
\[\begin{aligned} \min_{Z_1}\quad&g_1(Z_1)=Z_1\log Z_1+(s-Z_1)\log(s-Z_1)+\frac a2(Z_1-c_1)^2+b_1(Z_1-c_1)\\ \text{s.t.}\quad&0\leq Z_1\leq s,b_1=b \end{aligned}\]也就是将变量在坐标轴上右移$c_1$个单位。当$z\approx-c_1$,也就是$\alpha_i+z\approx0$,
\[s-Z_1=c_2-z\approx c_1+c_2=s\]距离0很远,也就避免了catastrophic cancellation。还有一个减运算,$Z_1-c_1$,但它不参加对数运算,因此相对误差可以接受,不会造成严重的数值计算问题。
类似的,当$z\approx c_2$,我们要将令$Z_2=c_2-z$,得到子问题的第二种等价形式:
\[\begin{aligned} \min_{Z_2}\quad&g_2(Z_2)=Z_2\log Z_2+(s-Z_2)\log(s-Z_2)+\frac a2(Z_2-c_2)^2+b_2(Z_2-c_2)\\ \text{s.t.}\quad&0\leq Z_2\leq s,b_2=-b \end{aligned}\]为了求解上面两个等价子问题,我们还是用牛顿法,先求一阶和二阶导数:
\[\begin{aligned} g'_t(Z_t)&=\log\frac{Z_t}{s-Z_t}+a(Z_t-c_t)+b_t\\ g''_t(Z_t)&=a+\frac{s}{Z_t(s-Z_t)} \end{aligned}\]现在考虑应该用$g_1(Z_1)$还是$g_2(Z_2)$,这里选择的依据是$z^*$离哪个界更近:
\[z^*\text{ closer to }\begin{cases} -c_1\\ c_2 \end{cases}\quad\rightarrow\quad\text{choose }\begin{cases} g_1(Z_1),\\ g_2(Z_2). \end{cases}\]还是那个问题,我们不知道$z^*$在哪儿,于是作者证明了下面的规律:
\[z^*\text{ closer to }\begin{cases} -c_1\\ c_2 \end{cases}\quad\leftrightarrow\quad z^*\begin{cases} \leq z_m\\ \geq z_m \end{cases}\quad\leftrightarrow\quad g'(z_m)\begin{cases} \geq0\\ \leq0 \end{cases}\quad\leftrightarrow\quad z_m\begin{cases} \geq-\frac ba\\ \leq -\frac ba \end{cases}\]根据这一规律,初始化方案变成了
\[Z_1^0=\begin{cases} \xi_0c_1&\text{if }c_1\geq\frac s2,\\ c_1&\text{otherwise} \end{cases}\quad Z_2^0=\begin{cases} \xi_0c_2&\text{if }c_2\geq\frac s2,\\ c_2&\text{otherwise} \end{cases}\]而$z^{k}+d$越界的处理方案也就变成了
\[c_2-Z_2^{k+1}=\xi(c_2-Z_2^{k+1})+(1-\xi)c_2\]即
\[Z_2^{k+1}=\xi Z_2^k\]由此得到下面的算法:

完整的算法过程
前面提到,不同于SVM,LR对偶问题的初始点无法设置为$\pmb 0$,一种朴素的初始化方法是将所有元素设为$\frac C2$,但实验表明虽然LR对偶问题没有稀疏性,但很多$\alpha_i$都是很小的。考虑最优性条件,即最优的$(\pmb w,\pmb\alpha)$满足
\[\alpha_i=\frac{C\exp(-y_i\pmb w^T\pmb x_i)}{1+\exp(-y_i\pmb w^T\pmb x_i)},\forall i\]显然随着算法进行,指数项$\exp(-y_i\pmb w^T\pmb x_i)$趋近于0,那么$\alpha_i$也会接近0,因此我们应当将初始向量设为很小的值,考虑
\[\alpha_i=\min(\epsilon_1 C,\epsilon _2),\forall i.\]其中$\epsilon_1$和$\epsilon_2$都是小于1的小正数。作者在这里引用了2005年的论文,其中的观点是当$y_i=-1$时,将$\alpha_i$初始化为$C/l^{-}$,也是就$C$除以负样本个数;当$y_i=1$时则令$\alpha_i=C/l^+$。上式中的$\epsilon_1C$就对应这个观点,而$\epsilon_2$的设置是因为作者觉得初始值不应完全受$C$影响($C$如果太大,初始值就不小了)。
注意这里的初始化是$\pmb\alpha$的初始化,之前很大篇幅论述的是求解子问题中$z$的初始化。
当构建子问题时,如果$\alpha_i\approx C$,那么前面提到的数值优化问题又会出现在计算$c_2=C-\alpha_i$的时候。为了解决这一问题,可以考虑$Z_2$的定义
\[Z_2=c_2-z=C-\alpha_i^{\text{old}}-z=C-\alpha_i^{\text{new}}\]因此,如果上一轮对第$i$个坐标分量更新时采用的是最小化$g_2(Z_2)$,那么这一轮构造子问题时,$c_2$可以直接用$Z_2$的值;而如果上一轮是最小化$g_1(Z_1)$,我们用$Z_2=s-Z_1$去求$c_2$,同样可以避免数值计算问题。这对应了上面的算法4为何同时返回$Z_1^k$和$Z_2^k$。
下图的算法是整个求解LR对偶算法的过程:

最后,作者通过定理6,证明了上述算法是线性收敛的:
定理6:算法5生成的序列$\{\pmb\alpha^s\}$会收敛到唯一的全局最优解$\pmb\alpha^*$,同时存在$0<\mu<1$和一个$s^0$使得(设目标函数为$D^{\text{LR}}$)
\[D^{\text{LR}}(\pmb\alpha^{s+1})-D^{\text{LR}}(\pmb\alpha^*)\leq\mu(D^{\text{LR}}(\pmb\alpha^{s})-D^{\text{LR}}(\pmb\alpha^*)),\forall s\geq s_0\]