从二项分布开始
我们来复习下概率统计的内容,先从二项分布开始。二项分布属于离散分布,简单理解就是一件事情以$p$的概率发生,现在有独立$n$次随机实验,问该事件发生$k(0\leq k\leq n)$次的概率。我们将事件发生的次数记为随机变量$X$,我们称$X$满足参数为$n,p$的二项分布,简记为$X\sim B(n,p)$。我们可以直接计算概率:
\[\Pr\{X=k\}={n\choose k} p^k(1-p)^{n-k}\]我们尝试绘制出$k\sim\Pr(X=k)$的散点图:
import matplotlib.pyplot as plt
from scipy.special import comb
def plot_binary(n, p):
'''
绘制k和Pr(x=k)的关系曲线
'''
x = list(range(0, n + 1))
y = [comb(n, k) * p**k * (1 - p)**(n - k) for k in x]
plt.scatter(x, y, label="$B({}, {})$".format(n, p))
plot_binary(20, 0.5) # B(20, 0.5)
plot_binary(40, 0.75) # B(40, 0.75)
plot_binary(30, 0.5) # B(30, 0.5)
plt.legend()
plt.show()
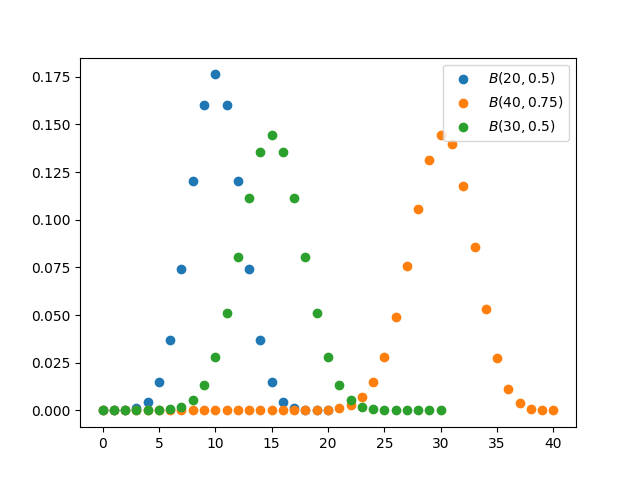
我们也不难计算出二项分布的均值和方差:令$X\sim B(n,p)$,则 \(\begin{aligned} E(X)&=np\\ D(X)&=np(1-p) \end{aligned}\)
二项分布与正态分布
观察上面的图像,发现二项分布散点图的轮廓与正态分布相似,这就是所谓的中心极限定理:当$n\to\infty$时,$B(n,p)$近似得服从$\mathcal{N}(np, np(1-p))$,正态分布的均值和方差就是原二项分布的均值方差。我们来简单验证一下:
import matplotlib.pyplot as plt
from numpy.core.function_base import linspace
from scipy.special import comb
import numpy as np
from math import pi
def plot_binary(n, p):
x = list(range(0, n + 1))
y = [comb(n, k) * p**k * (1 - p)**(n - k) for k in x]
plt.scatter(x, y, label="$B({}, {})$".format(n, p))
def plot_normal(mu, squared_sigma, x):
'''
绘制N(mu, sigma^2)的概率密度曲线
'''
C = 1 / np.sqrt(2 * pi * squared_sigma)
exp = np.exp(-(x - mu)**2 / (2 * squared_sigma))
plt.plot(x, C * exp, label="$N({}, {})$".format(mu, squared_sigma), color='orange')
n, p = 50, 0.5
mu, squared_sigma = n * p, n * p * (1 - p)
plot_binary(n, p)
plot_normal(mu, squared_sigma, x=linspace(0, 50, 100))
plt.legend()
plt.show()
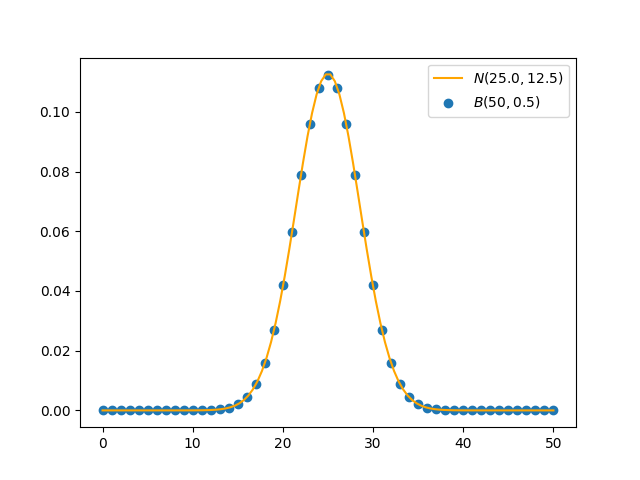
可见正态分布很好地拟合了二项分布。由此,我们可以通过计算正态分布函数来近似二项分布概率,以避免组合数计算带来的计算困难。这一操作也被称为“二项分布的正态逼近”。
当然逼近效果取决于参数$n$和$p$,维基百科提供的一个经验规则是$np>5,n(1-p)>5$。
连续性校正
在前面,我们发现二项分布的概率密度函数可以被正态分布的概率密度函数很好地逼近。我们现在想计算
\[\Pr(x\leq k)\]对于离散二项分布,其计算方法为累积求和:
\[\Pr(x\leq k)=\sum_{i=0}^k\Pr(x=i)\]而如果用正态分布,我们会去查表计算累积密度:
\[\Phi(\dfrac{k-\mu}{\sigma})=\int_{-\infty}^k\dfrac{1}{\sqrt{2\pi}\sigma}\exp(-\dfrac{(x-\mu)^2}{2\sigma^2}) \mathrm dx\]问题出在这里,我们用图像来说明:
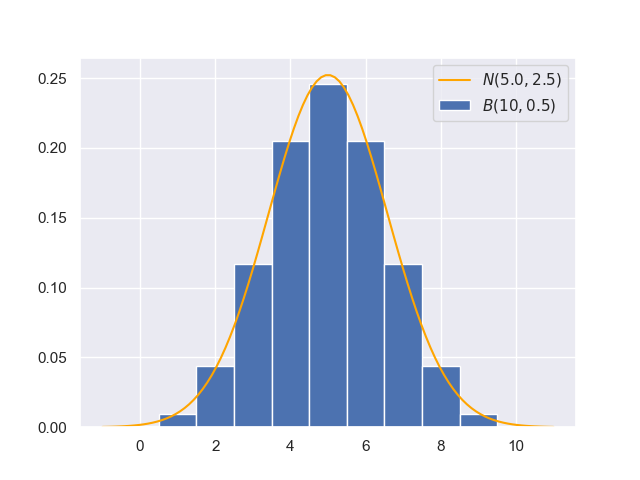
对于$n=10,p=0.5$的二项分布,假如我们想求$\Pr(x\leq 4)$,对应上图,就是将最左边5个长方形的面积相加(底为1,高为对应概率,不要忽略$x=0$的情况);而对于正态分布来说,就是$[-\infty,4]$区间上的曲边梯形的面积,也就是积分。这两者必然存在误差,我们可以用scipy.stats.norm.cdf绘制出正态分布的累积分布曲线,然后和二项分布进行比较:
import matplotlib.pyplot as plt
from scipy.special import comb
from scipy.stats import norm
import numpy as np
import seaborn as sns
sns.set()
def plot_binary_cdf(n, p):
x = list(range(0, n + 1))
y = np.array([comb(n, k) * p**k * (1 - p)**(n - k) for k in x])
plt.bar(x, np.cumsum(y), label="$B({}, {})$".format(n, p), width=1)
def plot_normal_cdf(mu, squared_sigma, x):
plt.plot(x,
norm.cdf(x, loc=mu-0.5, scale=np.sqrt(squared_sigma)),
label="$N({}, {})$".format(mu, squared_sigma),
color='orange',
)
n, p = 10, 0.5
mu, squared_sigma = n * p, n * p * (1 - p)
plot_binary_cdf(n, p)
plot_normal_cdf(mu, squared_sigma, x=np.linspace(-1, n + 1, 100))
plt.legend()
plt.show()
绘制的图像:
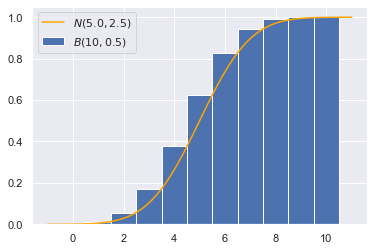
可以发现用正态分布估计的结果,要比真实结果要小,这是连续函数积分和离散函数求和的差异导致的。因此我们需要进行“连续性校正”,在计算累积密度时加上连续性修正因子0.5:
\[\Phi(\dfrac{k-\mu}{\sigma})\to\Phi(\dfrac{k+0.5-\mu}{\sigma})=\Phi(\dfrac{k-(\mu-0.5)}{\sigma})\]也就是用$\mathcal{N}(np+0.5,np(1-p))$的累积密度函数去逼近二项分布,我们重新画图:
def plot_correction_normal_cdf(mu, squared_sigma, x):
plt.plot(x,
norm.cdf(x, loc=mu - 0.5, scale=np.sqrt(squared_sigma)),
label="$N({}, {})$".format(mu, squared_sigma),
color='orange',
)
然后绘制:
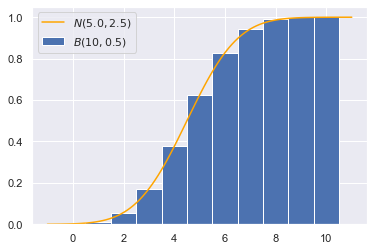
可以发现校正后的正态分布能够很好地估计二项分布的累积密度,这就是连续性校正的意义。