在之前的课程(《机器学习导论》)和自己的实践中,实现神经网络最后往往需要对一个激活函数指定其求导规则,比如当激活函数取Sigmoid的时候,总是要预先定义2个函数:
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(f):
return f * (1 - f)
来充当数学中Sigmoid函数及其导数。这样基于规则和先验知识的写法,在建立简单神经网络的时候是可行的,比如单隐层神经网络的实现,这里我设置激活函数全部为Sigmoid。但当网络变得复杂(层数增加,激活函数多样化)时,这种方法是不合理的。
在Pytorch等深度学习框架中,这些求导运算是由一种叫“自动求导”(Auto Differentiation)实现,本文主要探究其原理。
计算图
计算图是一个有向无环图,用来表示我们进行的运算过程,比如一个简单的加法
\[a+b\]对应的就是下面的计算图:
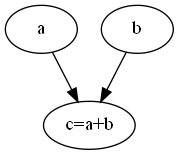
一个稍微复杂的计算图(计算$(wx-y)^2$):
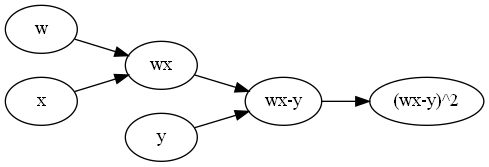
按照拓扑排序的顺序,给定$w,x,y$的值,沿着边的方向计算中间量的值,最后计算出$(wx-y)^2$,这一过程叫做前向传播。举例来说:设$w=1,x=2,y=3$,一个拓扑排序:
\[\begin{bmatrix} w&x&wx&y&wx-y&(wx-y)^2 \end{bmatrix}\]在前向传播开始前,除了输入节点外其余节点都没有值:
\[\begin{bmatrix} 1&2&?&3&?&? \end{bmatrix}\]按拓扑排序的顺序,从左往右计算空节点的值:
\[\begin{bmatrix} w&x&wx&y&wx-y&(wx-y)^2\\ 1&2&2&3&-1&1 \end{bmatrix}\]按照这样的思路,我们可以写出全连接神经网络的计算图,其中一层的结构是这样:
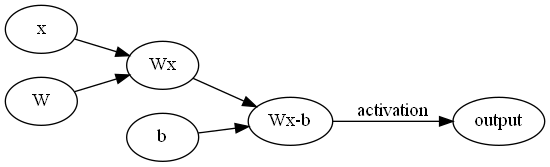
上一层的输出为$x$,通过权重矩阵作用,再减去一个偏置,然后通过激活函数激活,作为下一层的输入。
计算图的反向传播
前向传播是计算图最基础的功能,借助计算图实现对函数求偏导,才是我们想要的。
我们还是拿前面的$(wx-y)^2$计算图为例:

为了方便表达,我们约定
\[\begin{aligned} l_1&=wx\\ l_2&=wx-y\\ f&=(wx-y)^2\\ \end{aligned}\]正如名字那样,反向传播就是前向传播的“反向”,也就是按照拓扑排序的倒序:
\[\begin{bmatrix} f&l_2&y&l_1&x&w \end{bmatrix}\]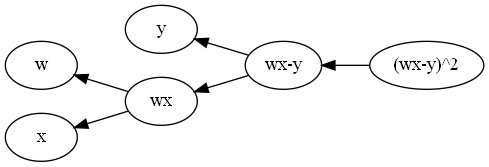
反向传播按照上面的顺序逐步求偏导,最后可以求出$\frac{\partial f}{\partial w},\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}$:
\[\begin{bmatrix} \dfrac{\partial f}{\partial f}&\dfrac{\partial f}{\partial l_2}&\dfrac{\partial f}{\partial y}&\dfrac{\partial f}{\partial l_1}&\dfrac{\partial f}{\partial x}&\dfrac{\partial f}{\partial w} \end{bmatrix}\]显然第一个偏导是1:
\[\begin{bmatrix} 1&\dfrac{\partial f}{\partial l_2}&\dfrac{\partial f}{\partial y}&\dfrac{\partial f}{\partial l_1}&\dfrac{\partial f}{\partial x}&\dfrac{\partial f}{\partial w} \end{bmatrix}\]对于第二项:
\[\begin{aligned} \dfrac{\partial f}{\partial l_2} &=\dfrac{\partial(wx-y)^2}{\partial (wx-y)}\\ &=2(wx-y)\\ &=2(1\cdot2-3)\\ &=-2 \end{aligned}\]第三项:
\[\begin{aligned} \dfrac{\partial f}{\partial y} &=\dfrac{\partial f}{\partial l_2}\dfrac{\partial l_2}{\partial y}\\ &=-2\dfrac{\partial(wx-y)}{\partial y}\\ &=2 \end{aligned}\]注意到在求第三项的时候,我们用到了第二项的结果,类似的,我们就可以推出剩下的偏导:
\[\begin{aligned} \dfrac{\partial f}{\partial l_1}&=\dfrac{\partial f}{\partial l_2}\dfrac{\partial l_2}{\partial l_1}\\ &=-2\dfrac{\partial(wx-y)}{\partial wx}\\ &=-2\\ \dfrac{\partial f}{\partial w}&=\dfrac{\partial f}{\partial l_1}\dfrac{\partial l_1}{\partial w}\\ &=-2\dfrac{\partial (wx)}{\partial w}\\ &=-2x\\ &=-4\\ \dfrac{\partial f}{\partial x}&=\dfrac{\partial f}{\partial l_1}\dfrac{\partial l_1}{\partial x}\\ &=-2\dfrac{\partial(wx)}{\partial x}\\ &=-2 \end{aligned}\]最后将结果收集起来:
\[\begin{bmatrix} \dfrac{\partial f}{\partial f}&\dfrac{\partial f}{\partial l_2}&\dfrac{\partial f}{\partial y}&\dfrac{\partial f}{\partial l_1}&\dfrac{\partial f}{\partial x}&\dfrac{\partial f}{\partial w}\\ 1&-2&2&-2&-4&-2 \end{bmatrix}\]这也就是计算图中反向传播(自动求导)的基本操作。