原文:http://proceedings.mlr.press/v101/gouk19a/gouk19a.pdf
这篇文章介绍了一种增量式学习决策树的方法:随机梯度树 (Stochastic Gradient Tree, SGT),也就是根据随机梯度去更新决策树。数据流场景往往要求模型对到来的数据立刻进行预测,而不是积攒了大量数据后再训练。
构造决策树
给定一个损失函数$\ell(y,\hat{y})$,其中$y$为真实标签,$\hat{y}$为模型的预测值,可以写作
\[\hat{y}=\sigma(f(\pmb x)),\]其中$\sigma$是一个optional的激活函数。在数据独立同分布的场景下,学习的总目标是最小化期望损失,而这一项是所采样的样本对应的损失函数值的无偏估计:
\[\mathbb{E}[\ell(y,\hat{y})]\approx\dfrac{1}{t-r}\sum_{i=r+1}^t\ell(y_i,\hat{y}_i),\]其中$\hat{y}_i$来自SGT, 也就是$f_t$。注意到如果$r=t-1$,那么这就是一个标准的数据流场景。在每一个时间步,我们希望找到一个对树的修改函数 (Modification) $u:\mathcal{X}\to\mathbb{R}$,在树执行这个函数后,期望损失可以降低。$u$可以是一个叶节点的分裂操作,也可以是一个对某个叶节点的预测值进行修改。那么决策树的更新操作可以形式化成
\[f_{t+1}=f_t+\mathop{\arg\min}\limits_{u}[\mathcal{L}_t(u)+\Omega(u)],\]其中
\[\mathcal{L}_t(u)=\sum_{i=r+1}^t\ell(y_i, f_t(\pmb x_i)+u(\pmb x_i)),\](后一项比较抽象,写成$(f_t+u)(\pmb x_i)$更好理解),且
\[\Omega(u)=\gamma|Q_u|+\frac\lambda2\sum_{j\in Q_u}v_u^2(j).\]这里的$\Omega$是正则化项,$Q_u\subset\mathbb{N}$是由$u$对树进行修改,关联的节点标识(identifiers)集。在相关文章中,叶节点与一个自然数绑定,而关联则可以是新产生的子节点,也可以是不分裂的父节点(这里其实不算父节点,因为没发生分裂)。$v_u:\mathbb{N}\to\mathbb{R}$是一个叶节点到预测值的函数,也就是$u$操作后叶节点上的预测值。所以该正则化项的目标是
- 减少生成的叶节点数量,或者说不倾向于分裂节点;
- 控制预测值的大小。
在数据流场景,或者说在线场景中,只有$\pmb x_t$所落到的叶子节点才会考虑是否分裂,而在此之前,落到这个节点上的样本则用来评估是否要分裂,以及如何分裂。为了对树进行优化,作者引入梯度提升,实际上这套和XGBoost的技术相通。考虑泰勒展开:
\[\mathcal{L}_t(u)\approx\sum_{i=r+1}^t[\ell(y_i, f_t(\pmb x_i))+g_iu(\pmb x_i)+\frac12 h_iu^2(\pmb x_i)],\]这里$g_i$和$h_i$是损失函数对$f_t(\pmb x_i)$的一阶和二阶导数。所以优化目标变成了最小化
\[\Delta\mathcal{L}_t(u)=\sum_{i=r+1}^t[g_iu(\pmb x_i)+\frac12 h_iu^2(\pmb x_i)]=\sum_{i=r+1}^t\Delta\ell_i(u),\]也就是由修改$u$引发的损失变化。由于我们只考虑$\pmb x_t$落入的叶节点,所以$u$的范围大大缩小到一个叶节点不同属性的分割。引入一些记号:定义一个潜在的分割:
\[u(\pmb x)=\begin{cases} v_u(q_u(\pmb x)),&\text{if }\pmb x\in\text{Domain}(q_u)\\ 0,&\text{otherwise} \end{cases}\]其中,$q_u$是一个映射:给定一个落在当前叶节点的样本$\pmb x$,假如我们对当前节点进行分割,$\pmb x_t$会下落到的新节点为$q_u$的输出,所以$v_u(q_u(\pmb x))$就是样本所落入的新节点的预测值。显然$q_u$的值域是$Q_u$的子集。而上式的$\text{Domain}(q_u)$就是会落入当前叶节点的样本$\pmb x$。令$I_u^j$为将落入由$u$诱导的新节点$j$的样本集合,那么优化目标重写为
\[\Delta\mathcal{L}_t(u)=\sum_{j\in Q_u}\sum_{i\in I_u^j}[g_iv_u(j)+\frac12 h_iv_u^2(j)],\]重排:
\[\Delta\mathcal{L}_t(u)=\sum_{j\in Q_u}[(\sum_{i\in I_u^j}g_i)v_u(j)+\frac12 (\sum_{i\in I_u^j}h_i)v_u^2(j)],\]我们再加入正则项,由此构成一个关于$v_u(j)$的二次函数:
\[\frac12(\sum_{i\in I_u^j}h_i+\lambda)v_u^2(j)+(\sum_{i\in I_u^j}g_i)v_u(j)\]那么最优的$v_u(j)$为
\[v_u^*(j)=-\frac{\sum_{i\in I_u^j}g_i}{\lambda+\sum_{i\in I_u^j}h_i}.\]切分数据
所以当选择分割的特征和阈值时,我们计算在不同特征和不同切分点下,所生成叶子节点的预测值,以及对应的损失变化量,选择最小的作为最后的特征和阈值。
- 对于连续值特征,我们采用CART那样的处理方式,前提是知道特征的值域,否则我们会在数据流开始时采样一系列数据来估计。
- 对于无序的离散属性(nominal),我们会选择所有的切分;
- 对于有序的离散属性(discretized),我们会选择所有的二分切割方式。
何时分裂
我们之前讨论的实际上是分割好不好,而不是要不要分割。著名的Hoeffding tree中使用霍夫丁不等式来判别。对于一个值域范围为$R$的属性,所采样的$n$个样本的平均值和期望之间,以$1-\delta$的概率满足:
\[\mathbb{E}[\bar{X}]>\bar{X}-\epsilon=\bar{X}-R\sqrt{\frac{\ln(1/\delta)}{2n}}\]现在,假如我们通过$\delta$和当前落在某叶节点的样本数$n$得到一个阈值$\epsilon$,设$\bar{L}$是假设进行分割后,在$n$个样本上的损失函数减小量的均值,一旦$-\bar{L}>\epsilon$,那么以$1-\delta$的置信度,该分割能够带来泛化风险的降低。但是霍夫丁不等式要求样本有界,这里就是要求损失函数的一阶和二阶导数有界,这使得SGT难以应用到任意的损失函数。因此,本文采用了$t$检验去决定是否需要分割。通过计算
\[t=\dfrac{\bar{L}-\mathbb E[\bar{L}]}{s/\sqrt{n}},\]其中$s$是样本的标准差。在零假设下,期望项为0。计算出来的$p$值如果小于置信度$\delta$,那么就可以进行分割。尽管$t$检验要求样本符合正态分布,损失函数不容易满足,但根据中心极限定理,当$n$足够大时就可以这样认为。按照下式计算方差:
\[\text{Var}(L_i)=\text{Var}(G_iv_u(j)+\frac12 H_iv_u^2(j)),\]这里$G_i$和$H_i$表示样本$i$的一阶和二阶导数,原文这里将$v_u(j)$视为一个常数,实际计算中需要考虑所有可能的$v_u(j)$。上式无法增量式计算,因为节点的值$v_u(j)$必须通过所有的样本才能计算得到。如果存储所有的一阶二阶导,那么带来存储上的开销。所以,上式分解成
\[\text{Var}(L_i)=v_u^2\text{Var}(G_i)+\frac14v_u^4\text{Var}(H_i)+v_u^3\text{Cov}(G_i, H_i).\]通过一些算法,比如Welford’s method和《Numerically stable, singlepass, parallel statistics algorithms.》中的一个算法,可以去增量式计算出方差和协方差。由于我们是要在新生成的各个叶子节点中计算综合的方差,这个可以通过篇文章的concurrent estimation algorithms来求出$s^2$。
如果每次有新样本出现时,我们都去验证是否收集了足够证据来证明分裂是合理,这个过程将会非常昂贵。在实践中,本文遵循在线决策树之前的范式,只有当落入叶节点的实例数量是某个用户指定参数的倍数时,才检查是否存在足够的证据来执行分割。与之前许多实现一样,该值默认设置为200。
也就是batch设置为200的倍数(如果第一次不分割,下一次考虑的就是400个样本,以此类推)。
应用到具体任务
如果我们想把SGT应用于(多)分类,那么和GBDT一样,我们学习多个SGT。对于一个$k$分类问题,对于样本$\pmb x_i$,它属于第$j$类的概率用softmax去表示:
\[\hat{y}_{i,j}=\dfrac{\exp(f_j(\pmb x_i))}{\sum_{c=1}^k\exp(f_c(\pmb x_i))},\]尽管看起来我们要训练$k$个SGT,但根据softmax的性质,我们只需要训练$k-1$棵树,设$f_k(\pmb x)=0$就行。在这里,损失函数为交叉熵,其原函数,一阶和二阶梯度如下:
\[\begin{aligned} \ell^{CE}(\pmb y,\hat{\pmb y})&=-\sum_{c=1}^ky_c\log(\hat{y}_c),\\ \dfrac{\partial\ell^{CE}}{\partial f_c(\pmb x)}&=\hat{y}_c-y_c,\\ \dfrac{\partial^2\ell^{CE}}{\partial f_c^2(\pmb x)}&=\hat y_c(1-\hat{y}_c).\\ \end{aligned}\]如果是回归任务,那么损失函数设置为平方损失,其各阶信息为
\[\begin{aligned} \ell^{SE}(y,\hat{y})&=\frac12(\hat{y}-y)^2,\\ \dfrac{\partial\ell^{SE}}{\partial f(\pmb x)}&=\hat{y}-y,\\ \dfrac{\partial^2\ell^{SE}}{\partial f^2(\pmb x)}&=1.\\ \end{aligned}\]文章的4.3提出用SGT解决多实例问题,这方面了解不多,所以这里省略。
实验
先看看这方面研究喜欢用什么数据集:
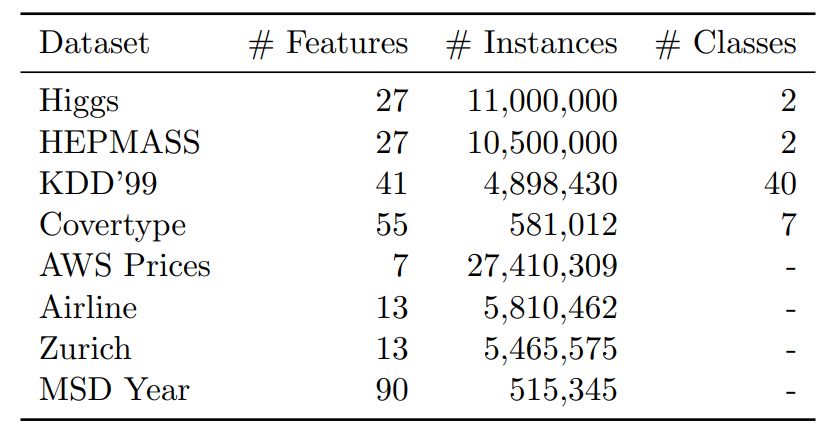
样本数最少都是50w。再看看对比方法,分类问题的对比方法是Hoeffding Tree (VFDT)和Extremely Fast Decision Tree (EFDT);回归问题的baseline是FIMT-DD和ORTO,分别出自Ikonomovska的《Learning model trees from evolving data streams》和《Speeding Up Hoeffding-Based Regression Trees with Options》,有兴趣的朋友可以阅读。最后的实验结果这里就不做展示,既然能发出来显然是意料之内的。
总结
本文介绍了SGT,一种增量式学习决策树的方法,它和XGBoost有相通之处,都是通过泰勒展开来判别分割。里面的方法和写法还是值得学习的,尤其是写惯了线性模型和核模型的我来说。