Introduction
图异常检测即在图结构上进行异常检测任务。随着图神经网络在实际应用中受到欢迎,图异常检测也在诈骗预防等领域收到重视。如果只考虑图节点的异常检测,那么在静态图、静态属性图和动态属性图中,静态属性图节点的异常检测受到了更多的研究:它的复杂度介于静态图和动态属性图之间。
受自编码器的启发,我们常常会将重构误差作为异常得分进行异常检测。因此,即使数据结构变成了图数据,很多模型依然会从这个方向入手,即从静态属性图中获取数据嵌入,然而试图重构结构信息(通常是邻接矩阵)和属性信息(即属性矩阵)。这也是当前该方向的主流方法。
本文将介绍基于上述思想的模型,上述模型的实现被包含在SAGOD中,这是笔者受PyGOD启发自实现的静态属性图节点异常检测的模型集。
Problem Definition
首先定义静态属性图(Static Attributed Graph):$G=\{V,E,\pmb X\}$,其中$V$和$E$分别是图的节点集和边集。除了拓扑结构外,每个节点还存在一个属性。属性矩阵$\pmb X=[x_i]_{n\times k}$包含了每个节点的属性向量。在更多时候,我们会将其表示成$G=\{\pmb A,\pmb X\}$,其中$\pmb{A}$是图邻接矩阵。我们希望得到这样一个函数$f(v_i),v_i\in V$,它返回一个异常得分。我们设定一个阈值$\tau$,集合$\{v_i\vert f(v_i)>\tau,\forall v_i\in V\}$中的节点为异常。
DOMINANT
DOMINANT用图卷积网络 (GCN) 来建模属性网络。GCN以拓扑结构和节点属性为输入,能够通过叠加多层线性单元和非线性激活函数来学习节点嵌入。
DOMINANT模型分成三个组件:
- 属性网络编码器:建模网络结构和节点属性,用GCN进行节点嵌入表示学习;
- 结构重构解码器:其目的是用学习到的节点嵌入来重建原始的网络拓扑结构;
- 属性重构解码器:它试图用所获得的节点嵌入来重建所观察到的节点属性。
然后,利用节点的重构误差来标记属性网络上的异常。模型结构如下图所示:
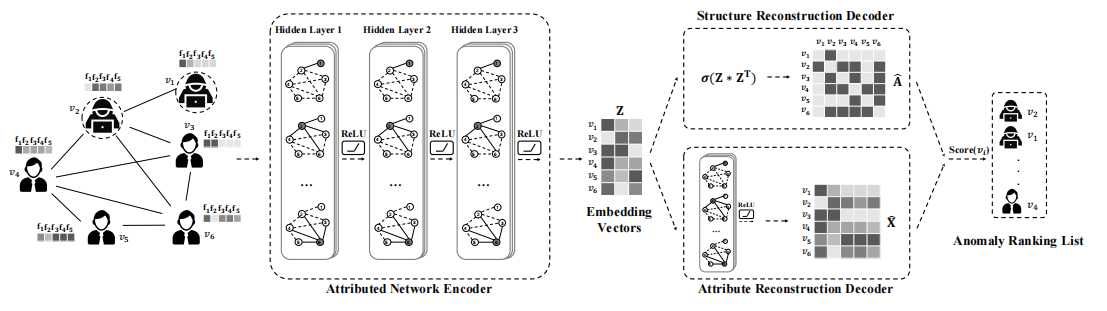
DOMINANT通过多层图卷积得到节点嵌入$\pmb Z$,基于它来重建邻接矩阵和属性矩阵:
\[\begin{aligned} \pmb{\hat{A}}&=\text{sigmoid}(\pmb{ZZ}^T)\\ \pmb{\hat{X}}&=\text{GCN}(\pmb Z) \end{aligned}\]优化重构误差:
\[\begin{aligned} \mathcal{L}&=(1-\alpha)\Vert\pmb{A}-\pmb{\hat{A}}\Vert_F^2+\alpha\Vert\pmb{X}-\pmb{\hat{X}}\Vert_F^2 \end{aligned}\]其中$\alpha$是一个超参数,表示我们更重视结构的异常还是节点的异常。类似的,每个节点的异常得分
\[score(i)=(1-\alpha)\Vert{\pmb a_i-\hat{\pmb a}_i}\Vert_2^2+\alpha\Vert{\pmb x_i-\hat{\pmb x}_i}\Vert_2^2\]AnomalyDAE
和DOMINANT将单个级联的GCN作为属性网络编码器不同,AnomalyDAE由结构自动编码器和属性自动编码器组成,分别通过重构原始网络拓扑和节点属性,共同学习节点和属性的潜在表示。和DOMINANT相同,AnomalyDAE通过从结构和属性两个角度衡量节点的重构误差来检测网络中的异常。
模型结构如下图所示:
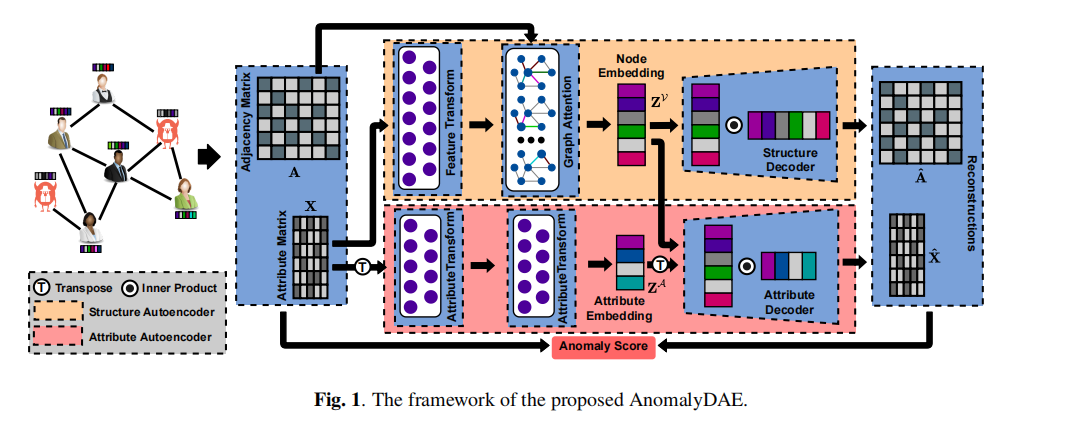
AnomalyDAE的重建步骤:
\[\begin{aligned} \pmb Z_{a}&=\text{FC}_1(\pmb{X}^T)\\ \pmb Z_{v}&=\text{GAT}(\text{FC2}(\pmb{X}))\\ \pmb{\hat{A}}&=\text{sigmoid}(\pmb{Z}_a\pmb Z_a^T)\\ \pmb{\hat{X}}&=\pmb{Z}_v\pmb{Z}_a^T \end{aligned}\]其中FC*表示全连接层,GAT表示图注意力层。AnomalyDAE的损失函数与DOMINANT类似,但多出对非零元素的重构误差施加更多的惩罚(文章原话):
\[\mathcal{L}=\alpha\Vert(\pmb A-\pmb{\hat{A}})\odot\pmb\theta\Vert_F^2+(1-\alpha)\Vert(\pmb X-\pmb{\hat{X}})\odot\pmb\eta\Vert_F^2\]其中$\odot$为阿达玛积,即元素对元素乘积。
\[\pmb\theta=\begin{cases} 1&\text{if }\pmb A_{ij}=0,\\ \theta&\text{otherwise}. \end{cases},\pmb\eta=\begin{cases} 1&\text{if }\pmb X_{ij}=0,\\ \eta&\text{otherwise}. \end{cases}\]$\theta$和$\eta$是大于1的超参数。同理,节点的异常得分为
\[score(i)=(1-\alpha)\Vert{(\pmb a_i-\hat{\pmb a}_i)\odot\pmb\theta_i}\Vert_2^2+\alpha\Vert{(\pmb x_i-\hat{\pmb x}_i)\odot\pmb{\eta}_i}\Vert_2^2\]ALARM
ALARM是一个将节点异常检测扩展到多视图的模型,作者认为将多视图的属性直接拼接在一起检测是不严谨的。模型结构:
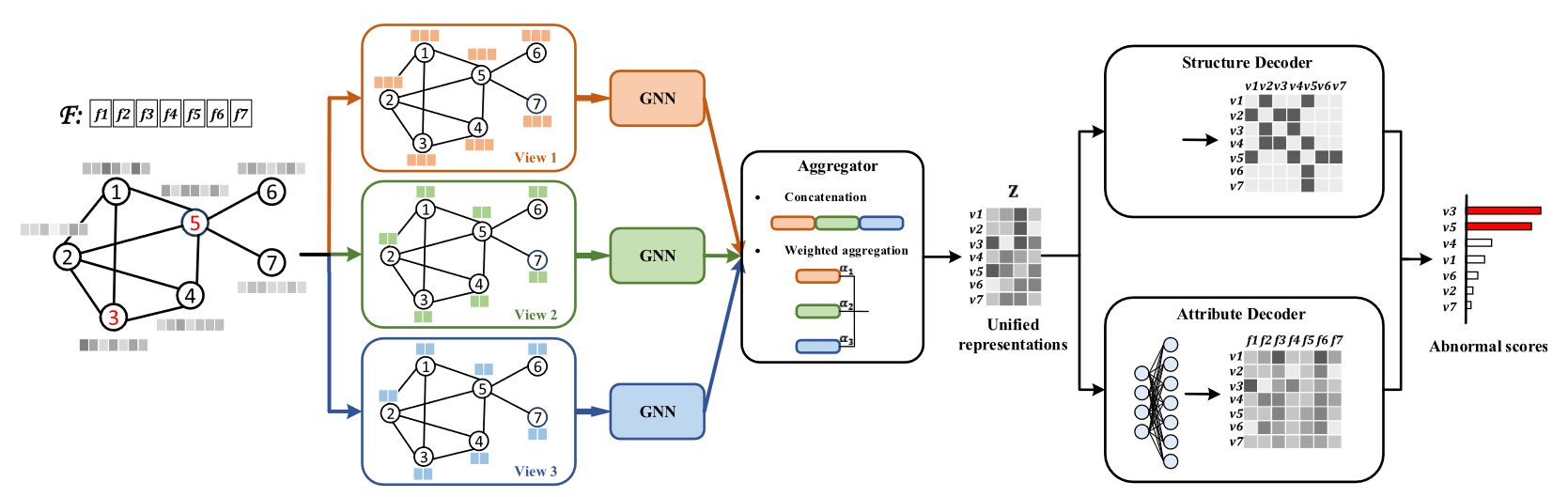
模型对每个视图的图数据用GNN进行图卷积,得到各视图的嵌入,然后进行聚合。聚合方案包括直接拼接和加权组合,聚合后得到整个图嵌入$\pmb{Z}$。ALARM使用和DOMINANT相同的方式重构$\pmb A$;使用一个全连接层,而不是DOMINANT中的GCN,将$\pmb Z$映射成$\pmb{\hat X}$。
在无权图中,$\pmb{\hat{A}}_{ij}$被用来建模有向边$e_{ij}$的存在概率,所以重构$\pmb{\hat{A}}$更应该是一个分类问题,所以优化时应使用交叉熵损失:
\[\mathcal{L}_s=\sum_{i=1}^n\sum_{j=1}^n-[\gamma\pmb{A}_{ij}\log\pmb{\hat{A}}_{ij}+(1-\pmb{A}_{ij})\log(1-\pmb{\hat{A}}_{ij})]\]其中$\gamma$是一个超参数,也就是损失函数的正样本权重。作者表示$\gamma$的设置是对精准率和召回率的权衡:$\gamma>1$会增加召回,$\gamma<1$会增加精准率。当然,对于带权图还是该使用之前的setting。
属性的重构误差和之前相同:
\[\begin{aligned} \mathcal{L}_a&=\Vert\pmb X-\pmb{\hat{X}}\Vert_F^2\\ \mathcal{L}&=\mathcal{L}_s+\mathcal{L}_s \end{aligned}\]异常得分遵从了之前的设置:
\[score(i)=(1-\alpha)\Vert{\pmb a_i-\hat{\pmb a}_i}\Vert_2^2+\alpha\Vert{\pmb x_i-\hat{\pmb x}_i}\Vert_2^2\]随着研究的深入,近期提出的一些属性图异常检测模型将不再只考虑重构,而是将其作为损失的一部分,但仍将其作为异常得分函数。我们接下来将介绍这些模型。
ComGA
ComGA模型全称为Community-Aware Attributed Graph Anomaly Detection。文章作者在文中提出了一个新颖的观点,即
GNN的卷积运算聚合邻居信息来表示节点,使得节点表示更加相似,不能有效区分正常节点和异常节点,从而导致次优结果。
也就是说,GCN的模式其实是不适合做异常检测的,但我觉得这是无奈之举,毕竟现在处理图数据的主流仍然是图卷积。
ComGA模型流程图:
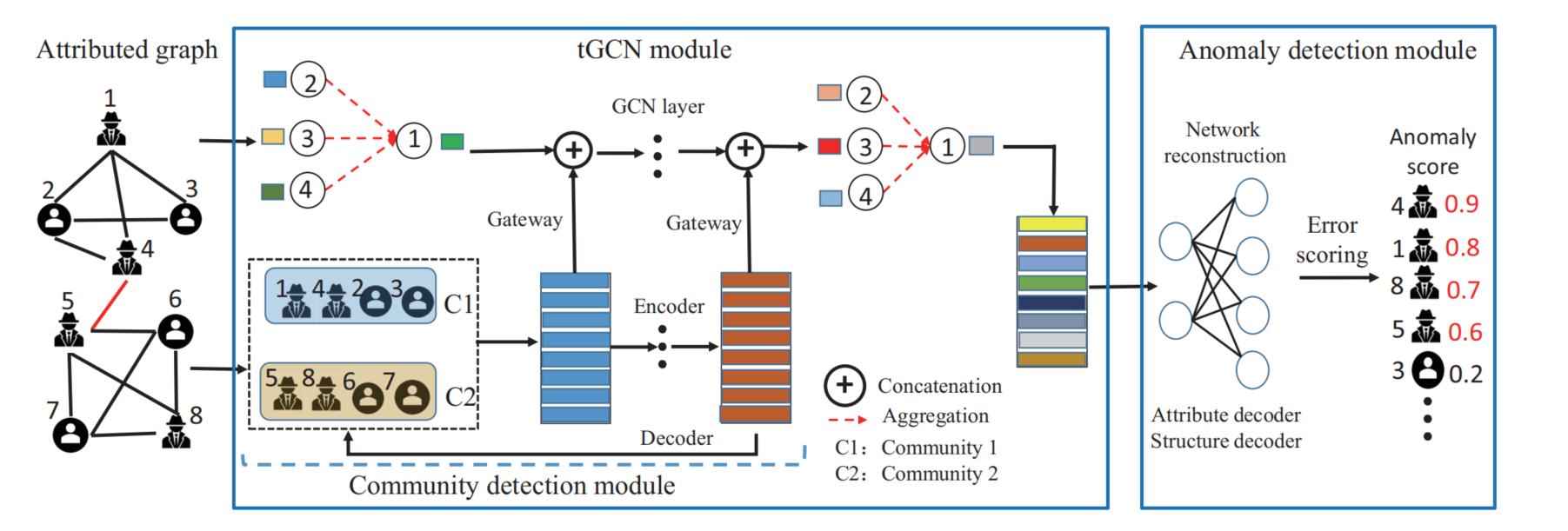
在介绍模型前,我们先引入模块度矩阵(Modularity Matrix)的概念,它常用于复杂网络的社区发现。设图$G$的邻接矩阵为$\pmb A$,那么它对应的模块度矩阵$\pmb B$为
\[b_{ij}=a_{ij}-\dfrac{k_ik_j}{2m}\]$k_i$和$k_j$分别是节点$i$和节点$j$的度,而$m=\frac12\sum_{i}k_i$表示边总数。模块度矩阵主要描述了不同社区的节点划分。也就是说它包含的社区信息。
ComGA用一个深度自编码器来编码和解码输入图的度矩阵,同时将各层的信息输入到(即加到)一个多层GCN的每一层。这样设计的目的是:基于多层GCN只能检测出局部的异常,而将模块度矩阵的信息加入然后去图卷积,这样模型就有了检测社区异常的能力。最终我们能得到网络嵌入$\pmb Z$。接着像DOMINANT那样,用一层GCN重构出$\pmb{\hat{X}}$,用sigmoid重构出$\pmb{\hat{A}}$。
至于损失函数,除了重构误差
\[\mathcal{L}_{rec}=(1-\alpha)\Vert\pmb{A}-\pmb{\hat{A}}\Vert_F^2+\alpha\Vert\pmb{X}-\pmb{\hat{X}}\Vert_F^2\]还包括了深度自编码器重构$\pmb B$的重构误差
\[\mathcal{L}_{res}=\Vert\pmb{B}-\pmb{\hat{B}}\Vert_{F}^2\]以及为了增强tGCN模块$\pmb Z$中最后一层的社区特定表示,作者设计了一个Community指导模块,将自动编码器模型和GCN模型紧密集成:
\[\mathcal{L}_{gui}=KL(\pmb Z\Vert\pmb H)\]其中$\pmb H$就是自编码器的潜在表示。所以总的损失函数为
\[\mathcal{L}=\mathcal{L}_{rec}+\mathcal{L}_{res}+\mathcal{L}_{gui}\]DeepAE
DeepAE这个名称容易让人误解成Deep Autoencoder的意思,但它实际上是一个图节点异常检测模型。DeepAE充分利用网络的内在信息,捕获局部和全局的关系信息,并使隐藏层中节点属性的语义信息与原始网络保持一致。此外,还引入了拉普拉斯锐化来保持正常节点和异常之间的差异。然后,我们通过利用这两种信息模式的重构误差来发现异常情况。
拉普拉斯锐化便是用于缓解上文提到GCN平滑而不利于异常检测的问题。我们知道图卷积的形式是
\[f(\pmb{\tilde{A}XW})\]也就是将归一化邻接矩阵,特征矩阵和权重矩阵相乘,再通过激活函数去激活。而拉普拉斯锐化则是尝试缓解平滑:
\[f\bigg(((1-\gamma)\pmb I+\gamma\tilde{\pmb{A}})\pmb{XW}\bigg)\]DeepAE模型如下图所示:
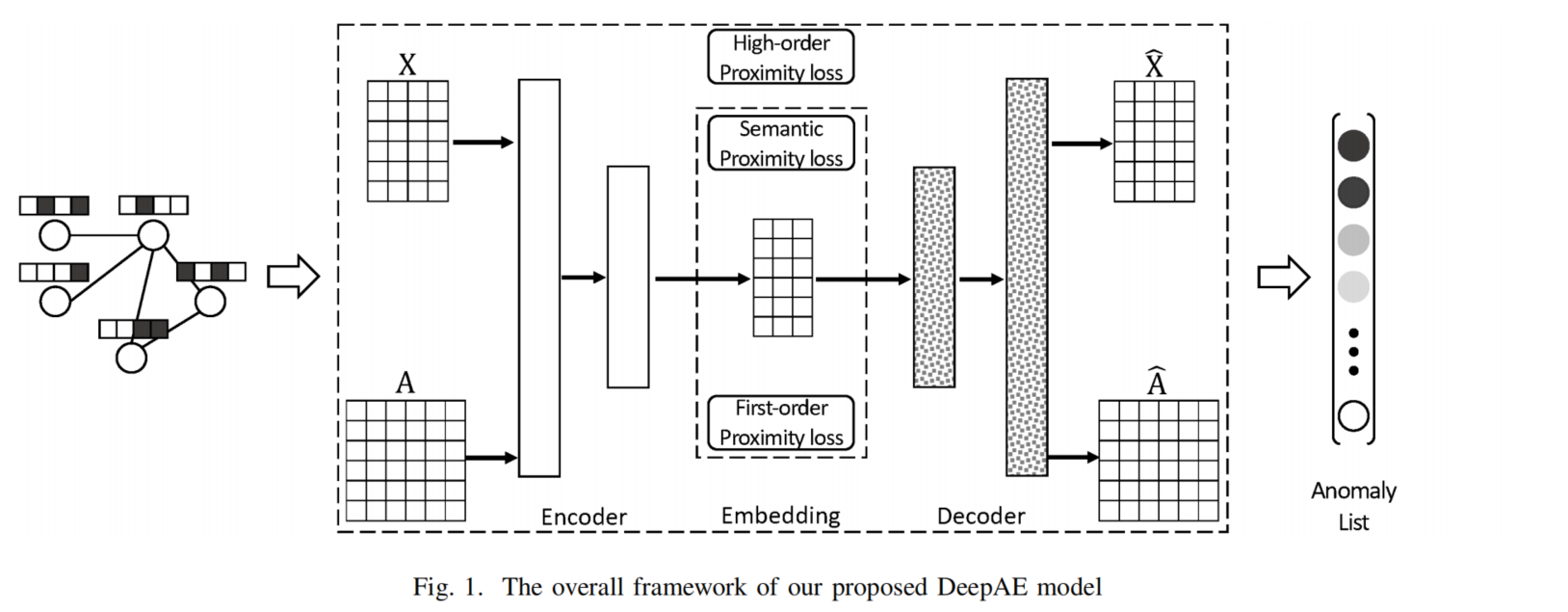
可以看出DeepAE还是属于比较简单的编码器-解码器架构。编码器是多层的普通GCN,而解码器则是带拉普拉斯锐化的GCN。用老方法重建$\pmb{\hat{A}}$和$\pmb{\hat{X}}$后,除了重构损失外,DeepAE还考率捕获局部的邻近性。受拉普拉斯特征映射的启发,作者定义了以下损失函数来约束一致性:
\[\mathcal{L}_f=\sum_{i,j=1}^n\hat{a}_{ij}\Vert\pmb{h}_i-\pmb{h}_j\Vert_2^2=2\text{tr}(\pmb H^T(\pmb D-\pmb{\hat{A}})\pmb H)=2\text{tr}(\pmb H^T\pmb{LH})\]原始网络中具有相似特征的节点在嵌入空间中也应该相同,从而从节点属性的角度保持局部邻近性。定义相似性
\[P(i,j)=\dfrac{sim_{ij}}{\sum_{a_{ij}\in\pmb A}sim_{ij}}\]$sim_{ij}$表示节点$i,j$的相似度,而
\[\hat{P}_{ij}=\text{sigmoid}(\pmb h_i\pmb h_j^T)\]是嵌入空间的相似性,两者应当尽可能接近:
\[\mathcal{L}_s=KL(P\Vert\hat{P})\propto-\sum_{a_{ij}\in\pmb{A}}sim_{ij}\log\hat{P}(i,j)\]因此优化目标为三种损失函数的和:
\[\mathcal{L}=\beta\Vert\pmb X-\pmb{\hat X}\Vert_F^2+\Vert\pmb A-\pmb{\hat A}\Vert_F^2+2\text{tr}(\pmb H^T\pmb{LH})-\sum_{a_{ij}\in\pmb{A}}sim_{ij}\log\hat{P}(i,j)\]异常得分函数为
\[score(i)=\beta\Vert\pmb x_i-\pmb{\hat x}_i\Vert_2^2+\Vert\pmb a_i-\pmb{\hat a}_i\Vert_2^2\]Conclusion
本文介绍了5种基于重构误差的属性图节点异常检测的模型,可以发现它们是基于自编码器异常检测思想的延伸。而随着僵硬的迁移无法带来更多提升,新模型加入了一些关于图性质的损失函数,比如模块度矩阵的重建。
在阅读多篇论文后,笔者的直观感觉是现有的模型仍然无法检测出异常的类型,也就是检测出局部、全局和社区异常。倘若未来提出的模型能够做到这一点,那么对该方向的研究无疑是很大的促进。
Reference
- Ding, Kaize, et al. “Deep anomaly detection on attributed networks.” Proceedings of the 2019 SIAM International Conference on Data Mining. Society for Industrial and Applied Mathematics, 2019.
- Fan, Haoyi, Fengbin Zhang, and Zuoyong Li. “AnomalyDAE: Dual autoencoder for anomaly detection on attributed networks.” ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2020.
- Peng, Zhen, et al. “A deep multi-view framework for anomaly detection on attributed networks.” IEEE Transactions on Knowledge and Data Engineering (2020).
- Luo, Xuexiong, et al. “ComGA: Community-Aware Attributed Graph Anomaly Detection.” Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining. 2022.
- Zhu, Dali, Yuchen Ma, and Yinlong Liu. “Anomaly detection with deep graph autoencoders on attributed networks.” 2020 IEEE Symposium on Computers and Communications (ISCC). IEEE, 2020.