在《Learning with Feature Evolvable Streams》一文中,作者提出了一种在线学习场景,即随着时间推移,流数据的特征会发生变化,如下图所示:

该场景在现实世界中同样存在,比如当多个传感器工作的时候,存在一些传感器故障和失灵,那么一些新的传感器会被启用。在这样的场景对数据进行学习的过程被称作特征演化流数据学习 (Feature Evolvable Streaming Learning, FESL)。
注意到上图的特征演化中,演化前后的特征不存在相交,而存在一个时期,有一小部分数据流同时拥有两个特征空间的数据。显然这个setting是必需的,否则我们将无法找出演化前后特征的关系。
一个naive的方法是,当特征流发生演化,那么我们就重新训练模型,将旧模型替换。这样显然会造成数据和模型的浪费。因此,一个关键问题是如何利用演化前的特征数据,以指导新特征下的机器学习。
本文的关键思想是,构造一个映射,来构建新旧特征空间。从而,我们可以利用演化后的特征数据重构演化前的特征。如此旧的模型可以复用。在拥有新旧模型的基础上,本文提出了两种方案,对两个模型进行集成,以获取更高的性能。
问题形式化
FESL更规范的流程如下图所示:
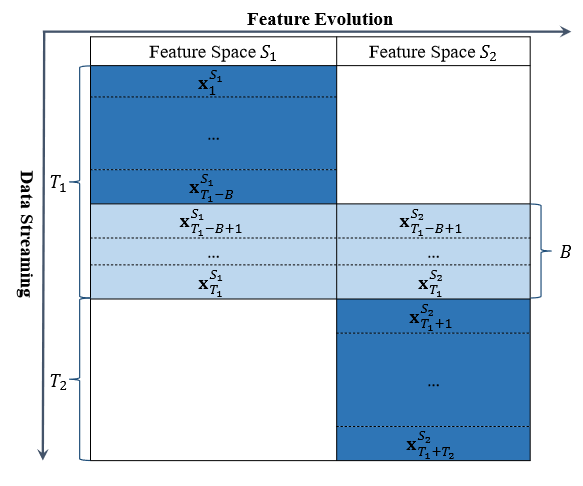
注意这只是一轮演化,FESL实际上允许多次特征变化。一次演化的步骤:
- 在$t=1,\cdots,T_1-B$,学习器每轮接受一条数据$\pmb{x}_t^{S_1}\in\mathbb{R}^{d_1}$,这是从特征空间$S_1$中采样得到的;
- 在$t=T_1-B+1,\cdots,T_1$,学习器每轮接受两个向量$\pmb{x}_t^{S_1}$和$\pmb{x}_t^{S_2}\in\mathbb{R}^{d_1}$,后者是从特征空间$S_2$采样得到的;
- 在$t=T_2+1,\cdots,T_1+T_2$,学习每轮接受一条数据$\pmb{x}_t^{S_2}$。
其中$B$是一个很短的时间。
我们设学习器为线性模型,因此设$\Omega_1\subseteq\mathbb{R}^{d_1}$和$\Omega_2\subseteq\mathbb{R}^{d_2}$是新旧模型的假设空间。设$\pmb{w}_{i,t}\in\mathbb{R}^{d_i},i=1,2$是预测第$t$轮样本时特征空间$S_i$下的模型。我们用对数损失和平方损失分别作为分类和回归问题的损失函数:
\[\begin{aligned} l_1(\pmb{w}^T\pmb{x},y)&=(1/\ln2)\ln(1+\exp(-y(\pmb{w}^T\pmb{x})))\\ l_2(\pmb{w}^T\pmb{x},y)&=(y-\pmb{w}^T\pmb{x})^2 \end{aligned}\]算法
首先要考虑如何构建两个特征空间的联系,即$\psi:\mathbb{R}^{d_2}\to\mathbb{R}^{d_1}$。考虑到两特征空间交错的时间$B$很短,无法学习更复杂的关系,所以只学习一个线性映射,即求解最小二乘
\[\min_{\pmb M\in\mathbb{R}^{d_2\times d_1}}\quad\sum_{t=T_1-B+1}^{T_1}\Vert{\pmb{x}_t^{S_1}-\pmb{M}^T\pmb{x}_t^{S_2}}\Vert_2^2\]很容易解出
\[\pmb M_*=\bigg(\sum_{t=T_1-B+1}^{T_1}\pmb{x}_t^{S_2}{\pmb{x}_t^{S_2}}^T\bigg)^{-1}\bigg(\sum_{t=T_1-B+1}^{T_1}\pmb{x}_t^{S_2}{\pmb{x}_t^{S_1}}^T\bigg)\]所以按照算法1,在第$T_1$轮时就可以得到最优的$\pmb M_{*}$,以及$S_1$上的模型:

其中第三、四行是一个在线学习的梯度下降优化。在$T_1$轮之后,我们就要计算两个参数为$\pmb{w}{1,t}$和$\pmb{w}{2,t}$的模型:
\[\begin{aligned} f_{1,t}&=\pmb{w}_{1,t}^T(\psi(\pmb{w}^{S_2}_t))\\ f_{2,t}&=\pmb{w}_{2,t}^T\pmb{x}_t^{S_2} \end{aligned}\]集成算法
论文提出了两种充分利用两个模型的集成算法:加权组合 (FESL-c) 和动态选择 (FESL-s)。先看加权组合,即用将两个基学习器组合成新学习器:
\[\hat{p}_t=\alpha_{1,t}f_{1,t}+\alpha_{2,t}f_{2,t}\]基于下式更新权重:
\[\alpha_{i,t+1}=\dfrac{\alpha_{i,t}\exp(-\eta l(f_{i,t},y_t))}{\sum_{j=1}^2\alpha_{j,t}\exp(-\eta l(f_{j,t},y_t))}\]其中$\eta$是超参数。算法如下图所示:

文章对该算法进行了分析,这里我们只写出结论。首先定义
\[L^{S_1}=\sum_{t=T_1+1}^{T_1+T_2}l(f_{1,t},y_t),L^{S_2}=\sum_{t=T_1+1}^{T_1+T_2}l(f_{2,t},y_t)\]而$L^{S_{12}}$是集成模型的累积损失:
\[L^{S_{12}}=\sum_{t=T_1+1}^{T_1+T_2}l(\hat{p}_t,y_t)\]定理1:对于取值为$[0,1]$的凸损失函数$l$,$\forall T_2>1,y_t\in\mathcal{Y}$,令$\eta_t=\sqrt{8\ln2/T_2}$,我们有
\[L^{S_{12}}\leq\min(L^{S_1},L^{S_2})+\sqrt{\frac{\ln2}2T_2}\]也就是说,集成模型的能力与两个base模型中最优的模型差不多。
集成模型的前提是基学习器都不差,但在FESL问题中,由于在线学习的背景,我们无法保证模型的性能满足这一前提。因此,动态选择方法不是集成,而是每轮选出最好的学习器去预测。选择的准则即学习器权重:
\[p_{i,t}=\dfrac{\alpha_{i,t-1}}{\alpha_{1,t-1}+\alpha_{2,t-1}}\]哪个权重大就用哪个模型。此时权重更新方案需要改进:
\[\begin{aligned} v_{i,t}&=\alpha_{i,t-1}\exp(-\eta l(f_{i,t},y_t))\\ \alpha_{i,t}&=\delta\frac{W_t}2+(1-\delta)v_{i,t},i=1,2, \end{aligned}\]其中$W_t=v_{1,t}+v_{2,t},\delta=1/(T_2-1),\eta=\sqrt{8/T_2(2\ln2+(T_2-1)H(1/(T_2-1)))}$,而$H(x)=-x\ln x-(1-x)\ln(1-x)$,即二分类交叉熵损失。
在算法分析的环节,文中指出,在$t>T_1$阶段的初期,由于旧模型已经学习了部分数据,性能是比新模型要好的,但随着$S_2$特征空间数据的增加,新模型最终会超过旧模型。设在$s$轮后新模型超过旧模型,那么采用动态选择策略下的损失
\[L^s=\sum_{t=T_1+1}^sl(f_{1,t},y_t)+\sum_{t=s+1}^{T_2}l(f_{2,t},y_t)\]显然
\[\min_{T_1+1\leq s\leq T_1+T_2}L^s\leq \min_{i=1,2}L^{S_i}\]定理2:
\[L^{S_{12}}\leq\min_{T_1+1\leq s\leq T_1+T_2}L^s+\sqrt{\frac{T_2}2(2\ln2+\frac{H(\delta)}{\delta})}\]定理2构建了两种算法的桥梁,同时构造了比定理1更紧的界。
实验
由于特征演化学习的情景特殊,所以看一下作者如何做实验也是挺有必要的。作者选了30个数据集,其中9个是合成的。对于非合成数据集,作者是把特征进行划分,作为$S_1$和$S_2$;对于合成数据集,作者用一个随机高斯矩阵将数据集的原特征空间$S_1$投影到新特征空间$S_2$。
实验用了三种比较方法:
- Naive Online Gradient Descent, NOGD. 即抛弃旧模型,只训练新模型;
- Updating Recovered Online Gradient Descent, ROGD-u,只用旧模型,旧模型会利用$S_2$特征空间的数据不断更新;
- Fixed Recovered Online Gradient Descent, ROGD-f,只用旧模型,而且旧模型不会随着演化后的数据更新。