前篇:https://welts.xyz/2022/08/15/gcn_graph_class/. 在那里,我们用图卷积网络实现了图分类任务。但在那里,我们进行优化时,每轮是计算全部数据集的平均损失,计算效率低,本文将讨论如何在图学习中使用batch,以及对其进行实验和分析。
Batch
考虑下面两张图:
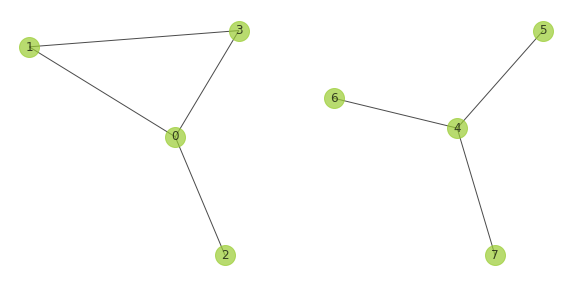
显然它们的邻接矩阵:
\[\pmb A_1=\begin{bmatrix} 0&1&1&1\\ 1&0&0&1\\ 1&0&0&0\\ 1&1&0&0\\ \end{bmatrix},\pmb A_2=\begin{bmatrix} 0&1&1&1\\ 1&0&0&0\\ 1&0&0&0\\ 1&0&0&0\\ \end{bmatrix}\]而如果将它们看作同一张图,邻接矩阵为
\[\pmb A=\begin{bmatrix} 0&1&1&1&0&0&0&0\\ 1&0&0&1&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 1&1&0&0&0&0&0&0\\ 0&0&0&0&0&1&1&1\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&1&0&0&0\\ \end{bmatrix}=\begin{bmatrix} \pmb A_1&\pmb O\\ \pmb O&\pmb A_2\\ \end{bmatrix}\]设两图的节点特征矩阵$\pmb X_1,\pmb X_2$。那么如果将它们看作一张图,那么该图的节点特征矩阵为
\[\pmb X=\begin{bmatrix} \pmb X_1\\\pmb X_2 \end{bmatrix}\]所以在多图的图节点分类任务中,我们原来是依次计算输出,然后计算损失去优化:
\[\begin{aligned} \hat{y}_1&=\text{READOUT}(\pmb{\hat{A}}_1\text{GCN}(\pmb{\hat{A}}_1\pmb X_1\pmb W^1)\pmb W^2)\\ \hat{y}_2&=\text{READOUT}(\pmb{\hat{A}}_2\text{GCN}(\pmb{\hat{A}}_2\pmb X_2\pmb W^1)\pmb W^2)\\ l&=\text{loss}(\hat{y}_1, {y}_1)+\text{loss}(\hat{y}_2, y_2) \end{aligned}\]而通过上面的归并,我们并行输出图表示:
\[\begin{aligned} \textbf{output}=\pmb{\hat{A}}\text{GCN}(\pmb{\hat{A}}\pmb X\pmb W^1)\pmb W_2 \end{aligned}\]但为了获取两个图各自的标签,我们需要分开进行READOUT,设第一张子图有$n_1$个节点,第二张子图有$n_2$个节点,那么
\[\begin{aligned} y_1&=\text{READOUT}(\textbf{output}_{0:n_1})\\ y_2&=\text{READOUT}(\textbf{output}_{n_1:n_1+n_2})\\ \end{aligned}\]如此,我们就可以实现图神经网络的多图Batch处理。在这里,我们主要是想通过图分类任务,来对图的批处理机制进行测试。
Batch in PyG
对于pytorch_geometric.data.Data形式存储的数据,其存储的不是邻接矩阵,而是$2\times$边数的edge_index张量,对应邻接矩阵中非零元素索引。上图的两张无向图如果分开看待,那么对应的edge_index分别是
而一旦我们将两张图看做同一张图,那么$\mathcal{E}_2$中的值将会加上第一张图的节点数,然后拼接在$\mathcal{E}_1$后,形成整图的edge_index:
而特征向量,我们只需要直接拼接即可。接下来我们进行实验:
from torch_geometric.datasets import TUDataset
from torch_geometric.data import Data
import torch
dataset = TUDataset(root='./ENZYMES', name='ENZYMES')
data1 = dataset[0]
data2 = dataset[1]
edge_index = torch.concat(
[data1.edge_index, data2.edge_index + data1.num_nodes],
axis=1,
)
x = torch.concat([data1.x, data2.x])
y = torch.concat([data1.y, data2.y])
data = Data(x=x, edge_index=edge_index, y=y)
我们可以将合并的data绘制出来:
g = nx.Graph()
g.add_edges_from(data.edge_index.numpy().T)
nx.draw(g, node_size=100)

可以发现data确实是两个图结的大图。由此,我们可以写出将多个图并成的Batch类:
class Batch:
def __init__(self, graph_list) -> None:
edge_index_list = []
x_list = []
y_list = []
ptr_list = []
self.num_nodes = 0
for graph in graph_list:
edge_index_list.append(graph.edge_index + self.num_nodes)
x_list.append(graph.x)
y_list.append(graph.y)
ptr_list.append(self.num_nodes)
self.num_nodes += graph.num_nodes
ptr_list.append(self.num_nodes)
self.edge_index = torch.concat(edge_index_list, axis=1)
self.x = torch.concat(x_list)
self.y = torch.concat(y_list)
self.ptr = torch.tensor(ptr_list)
这里的ptr成员存在的目的是为了将不同图节点进行区分,以进行READOUT。
为了节省存储空间,我们不再像以前那样存储各个图的$\pmb{\hat{A}}$,而是edge_index,所以我们对GCNConv进行修改:
from torch import nn
class GCNConv(nn.Module):
...
# 修改这个函数
def compute_coef(self, x : torch.Tensor, edge_index: torch.tensor):
hat_A = torch.zeros((x.shape[0], x.shape[0]))
hat_A[edge_index[0], edge_index[1]] = 1
if self.normalize:
if self.add_self_loops:
hat_A += torch.eye(x.shape[0])
if self.improved:
hat_A += torch.eye(x.shape[0])
tilde_D = 1 / torch.sqrt(torch.sum(hat_A, 1))
hat_A = tilde_D.reshape(-1, 1) * tilde_D * hat_A
return hat_A
Experiment
我们使用下面最简单的网络作为分类器:
class GCN(nn.Module):
def __init__(self, n_feature, n_label) -> None:
super().__init__()
self.gcn1 = GCNConv(n_feature, 64)
self.fc1 = nn.Linear(64, n_label)
def forward(self, batch: Batch):
gcn1 = self.gcn1(batch.x, batch.edge_index)
tuple_x = torch.split(gcn1, (batch.ptr[1:] - batch.ptr[:-1]).tolist())
readout = torch.concat(
[value.mean(
0,
keepdims=True,
) for value in tuple_x])
return self.fc1(F.leaky_relu(readout))
注意到我们需要用batch中存储的各图大小信息对数据进行分割,然后再进行READOUT。我们分别采用1,10,30,60,100的batch size进行实验,结果如下(数据进行了shuffle处理):
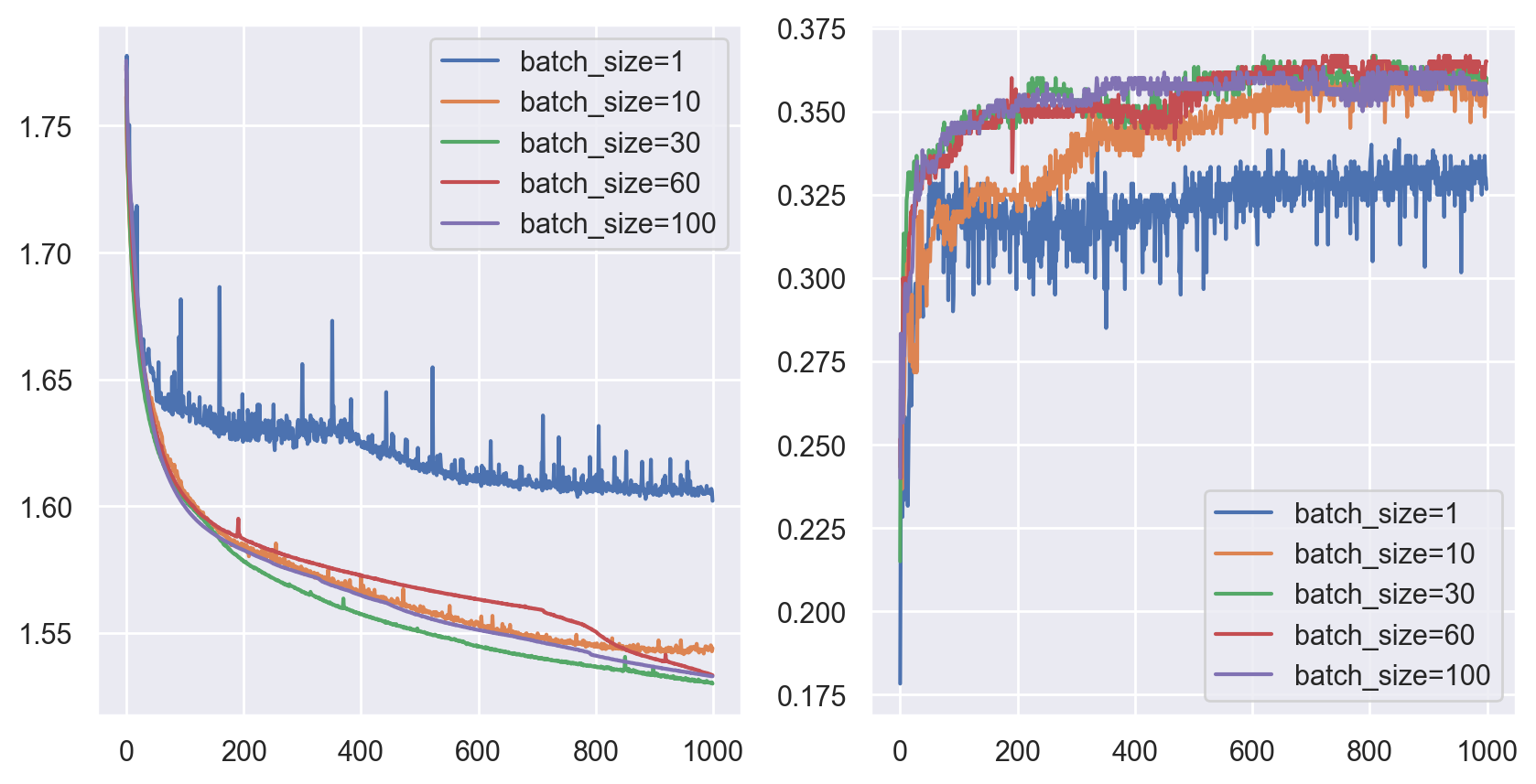
注意到10的batch size反而会影响收敛速度,同时带来损失和准确率的振荡。此外,60的batch size对应的训练效果最好。统计不同batch size下的运行时间:
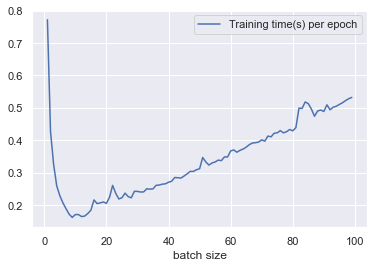
发现batch size为10附近训练最快。batch size越小,迭代次数就越多;batch size越大,单batch的计算代价越大。
Analysis
我们在这里进行一个简单的时间分析,设:
- batch size为$l$,总样本数为$L$;
- 样本平均的节点数为$n$,样本特征数为$h_0$;
- 网络结构为上文结构,隐藏层神经元数为$h_1$,图的类别数即最后一层的输出神经元数为$h_2$;
那么运行时间
\[\begin{aligned} t&=\dfrac{L}{l}(T_{\text{forward}}+T_{\text{backward}})\approx O(\frac{L}{l}T_{\text{forward}})\\ T_\text{forward} &=T_{\hat{A}}+T_{\hat{A}XW}+T_{\text{READOUT}}+T_\text{fc}\\ &=O(n^2l^2)+O(n^2l^2h_0+nlh_0h_1)+O(nlh_1)+O(lh_1+h_1h_2)\\ &=O(an^2l^2+bnl+cl+d)\\ t&=O(\dfrac{L}l(an^2l^2+bnl+cl+d))\\ &=O(an^2l+bn+c+\frac{d}{l}) \end{aligned}\]这里我们做了一些近似,比如考虑到计算图的固定,所以正向传播和反向传播的时间复杂度差不多。可以发现最后的时间复杂度是关于batch size的一个对勾函数,即$f(x)=ax+\frac bx+c$的形式,其图像与我们上面的时间图像的趋势完全一样。
Summary
我们在这里模拟了PyG等框架中的batch机制,并再次进行图分类实验,同时对运行时间进行了实验与分析。