Dropout和Batch Normalization是深度神经网络中常用的两种过拟合方法。本文简述两种技术(层)在神经网络中的技术细节,包括实现方法和训练模式和测试模式的区别。这里默认读者理解下面两张PPT的内容,即Dropout和BN的基本思想:


Dropout的前向反向传播
考虑我们神经网络的线性层(不考虑偏置项):
\[\pmb f=\pmb X_{l\times n_1}\pmb W_{n_1\times n_2}\]其中$l$是输入数据的batch size,$n_1$和$n_2$分别是线性层的输入神经元数和输出神经元数。$w_{ij}$表示输入层的第$i$个神经元指向输出层第$j$个神经元的权重。假如在数据输入之前我们对输入层进行Dropout,即令输入层的神经元随机失活(假设第$i$个神经元失活),那么等价于输入数据的第$i$个特征被设置为0,然后依然经过权重矩阵。
所以Dropout层的实现方法就是,给定丢弃概率$p$和该层神经元数$n$,我们对伯努利分布$Ber(p)$采样$n$次,得到一个向量
\[[x_1,x_2,\cdots,x_n]\in\{0,1\}^n\]对$i=1,\cdots,n$,如果$x_i=1$,我们就将$X$的第$i$列置为0然后输出,利用NumPy和PyTorch的数组索引机制,我们可以快速实现Dropout,这就是Dropout的前向传播。
Dropout的反向传播,即Dropout层的第$i$个输出对第$i$个输入的导数,根据Dropout的前向传播,如果$i$不是被置为0的列,那么导数就是
\[\dfrac{\partial y_i}{\partial x_i}=\dfrac{\partial x_i}{\partial x_i}=1\]否则就是0。
上面这种基础的Dropout方法使用的不广,现在更常用的是它的改进:Invert Dropout,大体的流程不变,唯一的区别就是,我们将随机列上的值取0后,对保留下来的列数据乘以一个$1/(1-p)$,即神经元保留概率的倒数,这是为了让Dropout层在训练阶段和测试阶段的输出期望保持一致。
因此相应的,在反向传播时,上式变成
\[\dfrac{\partial y_i}{\partial x_i}=\dfrac{\partial\frac1{1-p}x_i}{\partial x_i}=\frac1{1-p}\]Dropout的训练模式和测试模式
上面提到的Dropout的随机性只会出现在训练网络阶段,目的是抑制过拟合。所以在测试阶段Dropout层不会发挥作用,而是将输入的值原封不动地输出。这里我们就可以解释Invert Dropout中乘以$1/(1-p)$的原因了:考虑在训练阶段,如果没有Dropout层,或者说是测试阶段,线性层的第$j$个神经元输出的期望应当是:
\[\mathbb{E}[\sum_{i=1}^{n_1}x_iw_{ij}]\]而一旦有了Dropout层(训练阶段),其输出期望变成了
\[\begin{aligned} \mathbb{E}[\sum_{i=1}^{n_1}x_iq_iw_{ij}]&=\mathbb{E}[\sum_{i=1}^{n_1}x_iw_{ij}\mathbb{E}[q_i]]\\ &=(1-p)\mathbb{E}[\sum_{i=1}^{n_1}x_iw_{ij}] \end{aligned}\]其中$q_i\sim Ber(1-p),i=1,\cdots,n$。所以Dropout的训练阶段输出是要比没有Dropout的输出要小的,所以为了补偿,Invert Dropout选择将输出乘以一个$1/(1-p)$,使得训练和测试阶段的输出期望相同。
BN的前向和反向传播
Batch Normalization (BN)是加快网络训练速度,防止梯度消失和梯度爆炸的技巧。将一个Batch的训练数据输入到BN层时,BN层会将训练数据进行标准化。然后再通过伸缩参数$\gamma$和平移参数$\beta$对数据进行变换,这是为了防止数据原来的一些特征被标准化这一步骤消除了,即我们希望尽可能保留原数据的一些特征。
考虑BN层训练阶段的正向传播:
\[y=\gamma\dfrac{x-\mu}{\sqrt{\sigma^2+\epsilon}}+\beta\]$\gamma$和$\beta$都是可学习的参数,求导也很简单:
\[\begin{aligned} \dfrac{\partial y}{\partial\gamma}&=\dfrac{x-\mu}{\sqrt{\sigma^2+\epsilon}}\\ \dfrac{\partial y}{\partial \beta}&=1 \end{aligned}\]所以直接用梯度下降去学就行。
BN的训练模式和测试模式
和Dropout类似,BN层在训练时和测试时的表现也是不同的。我们不能使用测试集的标准差和均值来进行BN中的标准化,而应使用训练集中的统计量。这和数据数据标准化中,我们应该用训练集的标准差和均值来对测试集数据进行标准化。所以在测试模式中,正向传播的式子依旧是下面的形式:
\[y=\gamma\dfrac{x-\mu}{\sqrt{\sigma^2+\epsilon}}+\beta\]只不过$\mu$和$\sigma^2$都来源于训练集。这就迎来一个新问题,即如何获取训练集的均值和标准差。如果是选择对整个训练集进行计算,那么开销会大到无法承受。所以PyTorch选择使用滑动平均,即维护两个变量,running_mean和running_var,分别是均值和方差的滑动平均估计。在训练过程中,对于每一个Batch的输入,计算该Batch的均值$\mu$和方差$\sigma^2$后,将其加入到两个变量中:
$\beta$通常取$0.9$,$0.99$等值。我们将running_mean和running_var作为训练集均值和方差的近似,在测试阶段使用。
补充:Dropout和BN的位置
这里补充一下关于Dropout层和BN层插入位置的问题。前面讲Dropout的时候,我们是对输入随机失活,然后通过线性层,实际上我们也是将Dropout放在线性层之前,即激活函数层之后。
BN层对数据进行标准化,比如对Sigmoid函数:
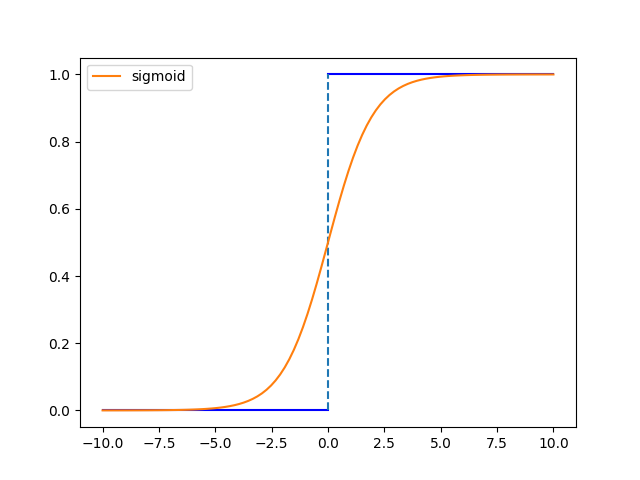
如果数据偏移零点太远,导数太小,造成梯度消失,这一点对$\tanh$函数是类似的。再考虑ReLU函数:
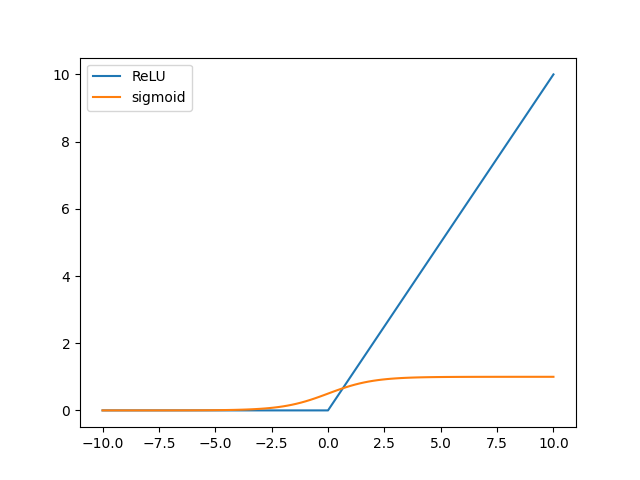
如果数据偏移零点太远(正数据),激活函数值太大,会在随后的Softmax等层造成溢出问题。因此,BN层最好放在线性层和激活函数之间,尤其是激活函数是Sigmoid和$\tanh$的情况。