引入
考虑线性等式约束和不等式约束的凸优化问题:
\[\begin{aligned} \min_{x}\quad&f_0(x)\\ \text{s.t.}\quad&f_i(x)\leq0,i=1,\cdots,m\\ &Ax=b \end{aligned}\tag{1}\]其中$f_0,\cdots,f_m$是二次可微的凸函数。$A\in\mathbb{R}^{p\times n}$,其中$\text{rank}(A)=p<n$。假定该问题可解,即存在$x^\ast$,我们设$p=f_0(x^\ast)$。同时假定该问题严格可行,使得KKT条件成立。令$\lambda^\ast\in\mathbb{R}^m$,$\nu^\ast\in\mathbb{R}^n$,它们与$x^\ast$一起满足KKT条件:
\[\begin{cases} Ax^\ast=b\\ f_i^\ast(x)\leq 0,i=1,\cdots,m\\ \lambda^\ast\succeq0\\ \nabla f_0(x^\ast)+\sum_{i=1}^m\lambda_i^\ast\nabla f_i(x^\ast)+A^T\nu^\ast=0\\ \lambda^\ast_if_i(x^\ast)=0,i=1,\cdots,m \end{cases}\tag{2}\]常用的下降方法难以求解该问题,比如牛顿法能够解决的是无约束凸优化,以及带等式约束的凸优化。内点法通过对问题进行修改,将问题转化为等式约束问题(注意这里的转换不是等价的,后面会提到)。我们这里讨论一种常用的内点法:障碍法。
障碍法
问题(1)等价于下述问题
\[\begin{aligned} \min_{x}\quad&f_0(x)+\sum_{i=1}^mI_{-}(f_i(x))\\ \text{s.t.}\quad &Ax=b \end{aligned}\tag{3}\]其中$I_{-}$为示性函数,
\[I_{-}(u)=\begin{cases} 0&u\leq0\\ +\infty&u>0 \end{cases}\]也就是说,问题(3)的目标函数对不满足条件的点施以极大的乘法。这种做法虽然保证问题(3)仍是凸优化问题,但其不可微性导致它仍是难以求解的。因此我们选用一个可微函数来近似替代示性函数:
\[\hat{I}_{-}(u)=-\frac1t\log(-u)\]其中$t>0$是确定近似精度的参数。下图是示性函数和不同参数的近似函数的图像:
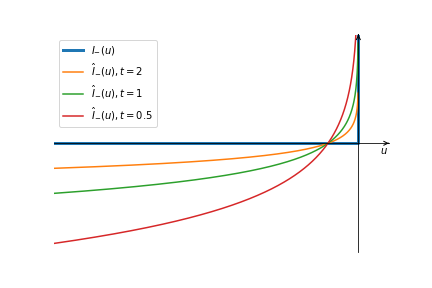
显然$t$越大,近似精度不断增加。我们用$\hat{I}_{-}$替换(3)中的示性函数:
\[\begin{aligned} \min_{x}\quad&f_0(x)+\sum_{i=1}^m-\frac1t\log(-f_i(x))\\ \text{s.t.}\quad &Ax=b \end{aligned}\tag{4}\]显然上式的目标函数是可微凸函数,可以用牛顿法求解。我们称
\[\phi(x)=-\sum_{i=1}^m\log(-f_i(x))\tag{5}\]成为问题(4)的对数障碍函数或对数障碍。直觉上,我们觉得$t$越大,近似精度增加,那么(3)和(4)最优解的差距会越小。对数障碍函数的梯度和Hessian矩阵也不难求得:
\[\begin{aligned} \nabla\phi(x)&=\sum_{i=1}^m-\frac1{f_i(x)}\nabla f_i(x)\\ \nabla^2\phi(x)&=\sum_{i=1}^m\frac1{f_i(x)^2}\nabla f_i(x)\nabla f_i(x)^T+\sum_{i=1}^m-\frac1{\nabla f_i(x)}\nabla^2f_i(x) \end{aligned}\tag{6}\]中心路径
为了形式上和求解上的方便,考虑下面的等价问题
\[\begin{aligned} \min\quad&tf_0(x)+\phi(x)\\ \text{s.t.}\quad&Ax=b \end{aligned}\tag{7}\]因为对于任意的正数$t$,问题(7)都存在一个最优解$x^\ast$,那么这种对应关系就可以构成一个函数$x^\ast(t),t>0$,我们称其为中心点,将这些点的集合定义为问题(7)的中心路径。中心路径上的所有点对应的解都是严格可行的,即存在一个$\hat\nu$使
\[\begin{cases} Ax^\ast(t)=b\\ f_i(x^\ast(t))<0,i=1,\cdots,m\\ t\nabla f_0(x^\ast(t))+\sum_{i=1}^m\frac{1}{-f_i(x^\ast(t))}\nabla f_i(x^\ast(t))+A^T\hat{\nu}=0 \end{cases}\tag{8}\]有趣的是,对上式最优一个条件稍加修改
\[\begin{aligned} \nabla f_0(x^\ast(t))+\sum_{i=1}^m\frac{1}{-tf_i(x^\ast(t))}\nabla f_i(x^\ast(t))+A^T\frac{\hat{\nu}}t&=0\\ \nabla f_0(x^\ast(t))+\sum_{i=1}^m\lambda_i^\ast(t)\nabla f_i(x^\ast(t))+A^T\hat\nu(t)&=0 \end{aligned}\tag{9}\]显然$\lambda_i^\ast(t)>0$。这样的取值是问题(1)的拉格朗日函数
\[\mathcal{L}(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\nu^T(Ax-b)\tag{10}\]的极小值,因此每个中心点都对应一个对偶可行解,因而给出最优值$p^\ast$的一个下界。拉格朗日函数的极小值:
\[\begin{aligned} L(x^\ast,\lambda^\ast,\nu^\ast)&=f_0(x^\ast(t))+\sum_{i=1}^m\lambda_i^\ast(t)f_i(x^\ast(t))+\nu^\ast(t)^T(Ax^\ast(t)-b)\\ &=f_0(x^\ast(t))-\frac1t\bigg[\sum_{i=1}^m\dfrac{\nabla f_i(x^\ast(t))}{f_i(x^\ast(t))}+\hat{\nu}(Ax^\ast(t)-b)\bigg]\\ &=f_0(x^\ast(t))-\frac mt \end{aligned}\tag{11}\]从而
\[f_0(x^\ast(t))-p^\ast\leq \frac{m}t\tag{12}\](12)告诉我们,随着$t$越大,$x^\ast(t)$会趋向于最优解。
障碍方法
现在,如果我们想求的$\epsilon$-次优解,我们只需要求解下面的问题
\[\begin{aligned} \min\quad&\frac m\epsilon f_0(x)+\phi(x)\\ \text{s.t.}\quad&Ax=b \end{aligned}\]该方法被称为无约束极小化方法,该方法对小规模、具有好的初始点,以及精度要求不高的任务可以取得好的效果,在其他情况下效果不佳。序列无约束极小化对无约束极小化方法进行扩充:每次用所获得的的最新点作为求解下一个问题的初始点,迭代求解直到满足精度要求。这一方法在今天被称为障碍方法或路径跟踪方法。算法的简单版本:

总结
我们对内点法(IPM)做了简单的介绍。撰写此文的原因是笔者在阅读论文时第一次遇到该方法,严格意义上说IPM这个名词是一年前接触的,当时笔者在修读《最优化方法》课程,瞥见教材的目录上的“内点法”字样,由于它是最后一章,授课时间有限,因此笔者对IPM并没有深入了解,所以这也相当于对当时未学的知识进行补偿。