本文主要介绍最大熵模型。笔者在阅读《Dual coordinate descent methods for logistic regression and maximum entropy models》一文时遇见该模型,之前在李航老师的《统计学习方法》中瞥见该模型的介绍,但并没有耐心读下去,因此重新学习一遍。
信息熵
这里的“熵”不是物理学中衡量混乱程度的熵,而是信息熵,虽然信息熵是由前者引申而来。类似的,信息熵表明一个随机变量的不确定性。设随机变量为$X$概率分布为$P(X)$,且
\[P(X=x_i)=p_i,i=1,\cdots,n\]那么我们想找到一个函数$f$来衡量某一随机事件发生的不确定性。显然概率越大,不确定性越小。同时也要求两独立事件共同产生的不确定性应当是各自不确定性之和。因此满足条件的函数为负对数函数:
\[f(p)=-\log p\]而对以随机变量而言,不应只考虑一种情况的不确定性,而是平均值。我们单一情况的不确定性的统计平均值(也就是期望)称作信息熵:
\[H(X)=\mathbb{E}[-\log p_i]=-\sum_{i=1}^np_i\log p_i\]考虑伯努利分布(0-1分布)的信息熵,其信息熵如下图所示:
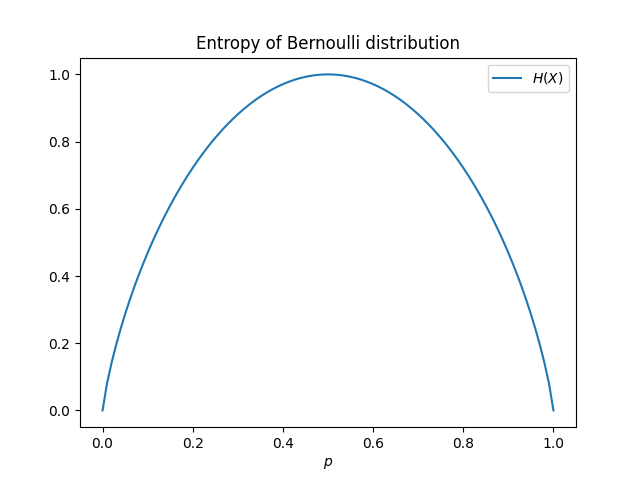
当$p$极大(随机变量为1的概率接近1)或$p$极小(随机变量为0的概率接近1)时,随机变量取值的不确定性越小;相反的,当$p=0.5$时,随机变量的取值等价于掷硬币,不确定性最大。根据拉格朗日乘子法(或其他方法),可以求解出当随机事件发生概率相同时:
\[p_i=\frac1n,i=1,\cdots,n\]也就是服从均匀分布时,随机变量的不确定性最大。
最大熵原理
回到我们熟悉的分类问题,假如我们对数据分布$P(X,Y)$一无所知,那么效果最好的做法其实就是随机地,等可能地分类,这是我们可以作出的唯一不偏不倚的选择,任何其它的选择都意味着我们增加了其它的约束和假设,显然这些约束和假设我们无法作出。等价的说法就是,在一无所知的情况下,(信息)熵最大的模型就是最优的模型。这里已经有最大熵原理的影子了。
在实际的分类任务中,我们必然不会对数据分布一无所知,而是掌握了未知分布的部分知识。在这种情况下,应选取符合这些知识(约束条件)且熵值最大的概率分布,这就是最大熵原理。在最大熵原理指导下求解出的分类模型便是最大熵模型。
最大熵模型
最大熵模型是判别式模型,也就是说,我们要求的是条件分布$P(Y\vert X)$。设训练集$\{(\pmb x_i,y_i\}_{i=1}^l$,学习的目的是用最大熵原理选择最好的分类模型。
现在考虑约束条件,即我们从数据中掌握的知识。定义特征函数$f(x,y)$:
\[f(x,y)=\begin{cases} 1,&当x,y满足某一事实.\\ 0.&不满足该事实. \end{cases}\]这样可以将数据集(比如文本)数学化。我们希望的是数据集中特征函数值的规律贴近真实分布中特征函数规律,也就是特征函数关于数据集分布(经验分布)的期望等于特征函数关于真实分布的期望。经验分布就是用数据频次作为概率的分布,用$\tilde{P}$表示:
\[\begin{aligned} P(X=x,Y=y)&=\frac{\nu(X=x,Y=y)}{l}\\ P(X=x)&=\frac{\nu(X=x)}{l}\\ \end{aligned}\]其中$\nu()$表示满足满足括号中条件的样本数。定义模型$P(Y\vert X)$关于$f$的期望$E_P(f)$:
\[E_P(f)=\sum_{x}\sum_{y}P(x,y)f(x,y)\approx\sum_{x}\sum_y\tilde{P}(x)P(y\vert x)f(x,y)\]和特征函数关于经验分布的期望$E_{\tilde P}(f)$:
\[E_{\tilde P}(f)=\sum_{x}\sum_y\tilde P(x,y)f(x,y)=\frac1l\sum_{x,y}f(x,y)\]因此两者相等便是模型需要满足的约束:
\[\sum_{x,y}\tilde P(x)p(y\vert x)f(x,y)=\sum_{x,y}\tilde{P}(x,y)f(x,y)\]考虑$n$个特征函数$f_i,i=1,\cdots,n$,那么模型就有$n$个约束,我们将满足约束的模型集合定义为$C$:
\[C=\{P\vert E_{P}(f_i)=E_{\tilde P}(f_i),i=1,\cdots,n\}\]前面提到,最大熵模型是判别式模型,因此我们的优化目标实际上是最大化条件熵,也就是
\[\begin{aligned} H(P) &=-\sum_{x}\tilde{P}(x)\sum_y P(y\vert x)\log P(y\vert x)\\ &=-\sum_{x,y}\tilde{P}(x)P(y\vert x)\log P(y\vert x) \end{aligned}\]下面给出最大熵模型需求解的优化问题的标准形式
\[\begin{aligned} \min_{P\in C}&\quad\sum_{x,y}\tilde{P}(x)P(y\vert x)\log P(y\vert x)\\ \text{s.t.}&\quad E_P(f_i)=E_{\tilde P}(f_i)\\ &\quad\sum_y P(y\vert x)=1 \end{aligned}\]最大熵模型的求解
定义上述优化问题的拉格朗日函数
\[\begin{aligned} \mathcal{L}(P,\pmb w,b)&=-H(P)+b\big[1-\sum_yP(y\vert x)\big]+\sum_{i=1}^nw_i\big(E_P(f_i)-E_{\tilde P}(f_i)\big)\\ \end{aligned}\]因为约束条件和优化函数都是凸函数,因此满足强对偶性,也就是
\[\min_{P\in C}\max_{\pmb w,b}\mathcal{L}(P,\pmb w,b)=\max_{\pmb w,b}\min_{P\in C}\mathcal{L}(P,\pmb w,b)\]因此可以求解右侧的对偶问题来求原问题。先求解$\min_{P\in C}\mathcal{L}(P,\pmb w,b)$,直接对$P(y\vert x)$求导
\[\begin{aligned} \dfrac{\partial\mathcal{L}}{\partial P}&=\sum_{x,y}\tilde{P}(x)[1+\log P(y\vert x)]-\sum_{y}b-\sum_{x,y}\bigg[\tilde{P}(x)\sum_{i=1}^nw_if_i(x,y)\bigg]\\ &=\sum_{x,y}\tilde{P}(x)\bigg[\log P(y\vert x)+1-b-\pmb w^T\pmb f(x,y)\bigg] \end{aligned}\]这里为了便于书写,我们将特征函数向量化,形成特征函数向量$\pmb{f}(x,y)$。令偏导为0,即
\[P(y\vert x)=\exp(\pmb w^T\pmb f(x,y)+b-1)=\frac{\exp(\pmb w^T\pmb f(x,y))}{\exp(1-b)}\]考虑概率和为1,不难得到
\[P_{\pmb w}(y\vert x)=\frac{\exp(\pmb w^T\pmb f(x,y))}{\sum_{y'}\exp(\pmb w^T\pmb f(x,y'))}\]然后利用优化算法最大化对偶函数,也就是
\[\max_{\pmb w}\quad\sum_{x,y}\tilde{P}(x,y)\pmb w^T\pmb f(x,y)+\sum_{x}\tilde{P}(x)\log\big(\sum_{y}\exp(\pmb w^T\pmb f(x,y)\big)\]设最优价为$\pmb w^*$,那么
\[P^*=P_{\pmb w^*}(y\vert x)=\frac{\exp(\pmb w^{*T}\pmb f(x,y))}{\sum_{y'}\exp(\pmb w^{*T}\pmb f(x,y'))}\]就是学习出来的最大熵模型。