引入
对于二次优化问题:
\[\min_{\pmb x}\quad f(\pmb x)=\frac12\pmb x^TA\pmb x-\pmb b^T\pmb x+c\]其中$A$是对称正定矩阵(SPD),我们很容易得到上述问题的解析解:
\[\begin{aligned} \dfrac{\partial f}{\partial\pmb x}&=A\pmb x-\pmb b=0\\ A\pmb x&=\pmb b\\ \pmb x&=A^{-1}\pmb b \end{aligned}\]可以发现该优化问题等价于求解线性方程组$A\pmb x=b$. 方程组的解与优化问题的最优解等价。我们可以通过高斯消元法来求出方程组的解,但这里我们想通过下降法来迭代求解。
最速下降法
下降法从当前点出发,寻找一个方向$\pmb{p}$,然后在该方向上寻找能够使目标函数下降最大的步长$\alpha$,也就是
\[\min_{\alpha}\quad f(\pmb x+\alpha\pmb p)\]我们还是可以得到$\alpha$的解析解:
\[\begin{aligned} \frac{\mathrm df(\pmb{x}+\alpha\pmb{p})}{\mathrm d\alpha} &=\frac{\mathrm df(\pmb{x}+\alpha\pmb{p})}{\mathrm d(\pmb x+\alpha\pmb p)}\frac{\mathrm d(\pmb{x}+\alpha\pmb{p})}{\mathrm d\alpha} \\ &=(A(\pmb x+\alpha\pmb{p})-\pmb b)^T\pmb p=0\\ \alpha&=-\frac{(A\pmb x-\pmb b)^T\pmb p}{\pmb{p}^TA\pmb p} \end{aligned}\]最速下降法每一次将当前点的负梯度方向作为下降方向,也就是$\pmb p=-(A\pmb x-b)$,设$\pmb r=b-A\pmb x$为剩余向量,代入得到
\[\alpha=\frac{\pmb r^T\pmb r}{\pmb r^TA\pmb r}\]于是对于第$k$次迭代,当前点$\pmb x_k$和目标点$\pmb x_{k+1}$的关系:
\[\pmb x_{k+1}=\pmb x_{k}+\alpha_k\pmb r_k\]因为
\[\begin{aligned} \pmb r_{k+1}^T\pmb r_k &=(\pmb b-A\pmb x_{k+1})^T\pmb r_k\\ &=(\pmb b-A(\pmb x_{k}+\alpha_k\pmb r_k))^T\pmb r_k\\ &=(\pmb r_k-\alpha_kA\pmb r_k)^T\pmb r_k\\ &=\pmb r_k^T\pmb r_k-\alpha_k\pmb r_k^TA\pmb r_k\\ &=0 \end{aligned}\]也就是说,相邻两次下降方向是正交的,就像下图这样:
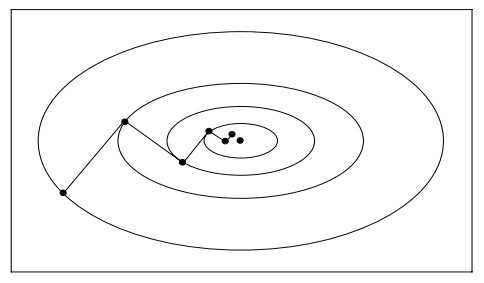
在该问题上使用最速下降方法有两个缺点:
- 迭代步数过大,收敛速度慢,而在极端情况下(条件数很大,也就是$A$的最大特征值和最小特征值的比值很大,此时椭球在某一个维度上会很扁),收敛速度会更慢;
- 当$\Vert\pmb r_k\Vert$很小时,计算会出现不稳定。
我们需要更好的迭代算法求解该问题。
共轭梯度法
共轭梯度法(Conjugate Gradient)是一种求解大型稀疏对称正定方程组十分有效的方法。我们仍选择一组搜索方向$\pmb{p}_0,\pmb{p}_1,\cdots$,但它们不再是具有正交性的$\pmb{r}_0,\pmb{r}_1,\cdots$。
首先我们引入共轭向量的概念:设$A$是对称正定矩阵,若$\mathbb{R}^n$中的向量组$\{\pmb p_0,\cdots,\pmb p_m\}$满足
\[\pmb p_i^TA\pmb p_j=0,\forall i,j\in[0,m],i\neq j\]那么我们称该向量组为一个$A$-共轭向量组或$A$-正交向量组。可以发现当$A=I$时,$A$-正交向量组正是一个一般的正交向量组。
回到优化问题,对于前$k$轮迭代,我们有
\[\begin{aligned} \pmb x_{k+1}&=\pmb x_k+\alpha_k\pmb p_k\\ \pmb x_k&=\sum_{i=0}^{k-1}\alpha_i\pmb p_i \end{aligned}\]初始方向可以设为$\pmb r_0$,而当$k\geq1$,我们希望确定$\pmb p_k$时满足
\[f(\pmb x_{k+1})=\min_{\alpha}\quad f(\pmb x_{k}+\alpha\pmb p_k)\]的同时(也就是$\pmb p_k$方向上最小),还希望
\[f(\pmb x_{k+1})=\min_{\pmb x\in\text{span}\{\pmb p_0,\cdots,\pmb p_k\}}f(\pmb x)\tag{*}\]也就是在所有已探索方向上都是最优的。这一点保证了之后的下降方向不会与之前的方向重复,而我们前面提到的最速下降无法保证这一点,可以参考上面的图像:$n=2$,而相邻下降方向正交,导致每隔一次迭代都会发生下降方向重复的问题,从而降低了收敛速率。
现在我们打算求解*式,将$\pmb x$进行分解:
\[\pmb x=\pmb y+\alpha\pmb p_k,\pmb y\in\text{span}\{\pmb p_0,\cdots,\pmb p_{k-1}\},\alpha\in\mathbb{R}\]从而我们有
\[\begin{aligned} f(\pmb x)&=f(\pmb y+\alpha\pmb p_k)\\ &=f(\pmb y)+\alpha\nabla f(\pmb y)^T\pmb p_k+\frac{\alpha^2}2\pmb p_k^T\nabla^2f(\pmb y)\pmb p_k\\ &=f(\pmb y)+\alpha(A\pmb y-\pmb b)^T\pmb p_k+\frac{\alpha^2}2\pmb p_k^TA\pmb p_k\\ \end{aligned}\]我们令交叉项为0,使得上式能够很好地对$\pmb y$和$\pmb\alpha$分别优化,也就是
\[\pmb y^TA\pmb p_k=0,\forall\pmb y\in\text{span}\{\pmb p_0,\cdots,\pmb p_{k-1}\}\]如果每一步迭代都这样选择$\pmb p_k$,那么向量组$\{\pmb p_1,\cdots,\pmb p_k\}$就是前面所说的$A$-共轭向量组。现在优化
\[\begin{aligned} \min_{\pmb x\in\text{span}\{\pmb p_0,\cdots,\pmb p_k\}}f(\pmb x) &=\min_{\pmb y}f(\pmb y)+\min_{\alpha}\frac{\alpha^2}2\pmb p_k^TA\pmb p_k+\alpha\pmb y^TA\pmb p_k-\pmb b^T\pmb p_k\\ \end{aligned}\]第一个问题的最优解就是$\pmb x_k$,第二个问题的最优解通过求导获得:
\[\alpha_k=\frac{\pmb p_k^T\pmb r_k}{\pmb p_k^TA\pmb p_k}\]我们获取了每一个迭代对应的步长,现在只需要出一个共轭向量组,这个共轭向量组的初始元素为$\pmb p_0=\pmb r_0$。由于共轭向量组并不唯一,不妨设
\[\pmb p_k=\pmb r_k+\beta_{t-1}\pmb p_{k-1}\]考虑$\pmb p_{k}A\pmb p_{k-1}=0$,解出系数
\[\beta_{k-1}=-\frac{\pmb p_{k-1}A\pmb r_k}{\pmb p_{k-1}^TA\pmb p_{k-1}}\]给定初始的位置$\pmb x_0$和方向向量$\pmb p_0=\pmb r_0$,求出$\alpha_0$,然后进行迭代得到$\pmb x_1$,计算出$\pmb r_1$,从而计算出$\beta_0$,得到新的共轭向量$\pmb p_1$,不断循环这样的过程得到序列$\{x_k\}$,这就是共轭梯度法。
简化计算
由于$\pmb r_i$具有正交性,必然有
\[\begin{aligned} \pmb r_{i+1}^T\pmb r_i &=(\pmb r_i-\alpha_iA\pmb p_i)^T\pmb r_i\\ &=\pmb r_i^T\pmb r_i-\alpha_i\pmb p_i^TA\pmb r_i\\ &=0\\ \alpha_i &=\frac{\pmb r_i^T\pmb r_i}{\pmb p_i^TA\pmb r_i}\\ &=\frac{\pmb r_i^T\pmb r_i}{\pmb p_i^TA(\pmb p_i-\beta_{i-1}\pmb p_{i-1})}\\ &=\frac{\pmb r_i^T\pmb r_i}{\pmb p_i^TA\pmb p_i} \end{aligned}\]类似的
\[\begin{aligned} \beta_{k-1} &=-\frac{\pmb p_{k-1}A\pmb r_k}{\pmb p_{k-1}^TA\pmb p_{k-1}}\\ &=-\dfrac{\pmb r_k^T(\pmb r_{k-1}-\pmb r_k)}{\alpha_i\pmb p_{k-1}^TA\pmb p_{k-1}}\\ &=\frac{\pmb r_{k}^T\pmb r_{k}}{\pmb r_{k-1}^T\pmb r_{k-1}} \end{aligned}\]最后算法
我们最终得到求解$A\pmb x=\pmb b$的算法,其中$A$是实对称正定矩阵。
\[\begin{aligned} &\text{CG}(A,\pmb b):\\ &\qquad\pmb x_0\gets\pmb 0\\ &\qquad\pmb r_0\gets\pmb b-A\pmb x_0\\ &\qquad\pmb p_0\gets\pmb r_0\\ &\qquad k\gets0\\ &\qquad\textbf{repeat}\\ &\qquad\qquad\alpha_k\gets\frac{\pmb r_k^T\pmb r_k}{\pmb p_k^TA\pmb p_k}\\ &\qquad\qquad\pmb x_{k+1}\gets\pmb x_k+\alpha_k\pmb p_k\\ &\qquad\qquad\pmb r_{k+1}\gets\pmb r_k-\alpha_kA\pmb p_k\\ &\qquad\qquad如果\pmb r_{k+1}足够小,则跳出循环\\ &\qquad\qquad\beta_k\gets\frac{\pmb r_{k+1}^T\pmb r_{k+1}}{\pmb r_{k}^T\pmb r_{k}}\\ &\qquad\qquad\pmb p_{k+1}\gets\pmb r_{k+1}+\beta_k\pmb p_k\\ &\qquad\qquad k\gets k+1\\ &\qquad \textbf{end} \end{aligned}\]$\pmb x_{k+1}$就是问题的解。