引言
我们在前面介绍了用随机傅里叶特征的方法求核函数的过程,而笔者在Kaslanarian/PySVM: 支持向量机模型(分类、回归和分布估计)的Python(numpy)实现 (github.com)实现了多个基于SMO算法支持向量机模型,其中的高斯核函数是基于直接计算实现的。因此,我打算将随机傅里叶特征(RFF)模块化,嵌入到SVM中,并进行性能与速度的比较。
RFF模块的设计
RFF模块类似于sklearn中的PCA模块,也就是基于以下三步进行变换:
rff = RFF()
rff.fit(X)
Z = rff.transform(X)
这一点可以通过继承sklearn.base.BaseEstimator实现:
class RFF(BaseEstimator):
def __init__(self, gamma=1, D=10000) -> None:
'''
Parameter
---------
gamma : 高斯核函数的参数
D : 抽样次数,等价于随机特征数
'''
super().__init__()
self.gamma = gamma
self.D = D
def fit(self, X):
self.n_features = np.array(X).shape[1]
self.w = np.sqrt(
self.gamma) * np.random.normal(size=(self.D, self.n_features))
self.b = 2 * np.pi * np.random.rand(self.D)
return self
def transform(self, X):
X = np.array(X)
Z = np.sqrt(2 / self.D) * np.cos(X @ self.w.T + self.b)
return Z
RFF的嵌入
在模型参数中加入rff和D两项,分别表示是否用RFF法计算核函数,以及随机特征数,然后对核函数注册进行修改:
if self.rff:
rff = RFF(gamma, self.D).fit(X)
rbf_func = lambda x, y: rff.transform(x) @ rff.transform(y).T
else:
rbf_func = lambda x, y: np.exp(-gamma * (
(x**2).sum(1).reshape(-1, 1) + (y**2).sum(1) - 2 * x @ y.T))
如果模型选用了rbf核,则将rbf_func作为核函数,其他不变:
self.kernel_func = {
"linear": lambda x, y: x @ y.T,
"poly": lambda x, y: (gamma * x @ y.T + coef0)**degree,
"rbf": rbf_func,
"sigmoid": lambda x, y: np.tanh(gamma * (x @ y.T) + coef0)
}[self.kernel]
事实上,分类SVM、回归SVM以及异常检测SVM都可以嵌入RFF模块。
性能测试
我们从耗时和准确率两个角度来对模块进行测试和分析。
首先是性能测试,以分类任务为例,采用sklearn中的digits数据集,1797条数据,10个类别:
| 核种类 | 准确率 |
|---|---|
| $\text{RBF}$ | $97.96\%$ |
| $\text{RFF},D=1$ | $41.48\%$ |
| $\text{RFF},D=10$ | $76.30\%$ |
| $\text{RFF},D=100$ | $96.48\%$ |
| $\text{RFF},D=1000$ | $97.41\%$ |
| $\text{RFF},D=10000$ | $97.41\%$ |
可以发现,当采样数达到$100$时,RFF下的SVM就已经和RBF下的SVM性能接近;当采样数到达1000时,分类性能基本相同。
再来看回归任务,以波士顿房价数据集为例,506条数据,13个特征:
| 核种类 | $R^2$ |
|---|---|
| $\text{RBF}$ | $0.662$ |
| $\text{RFF},D=1$ | $0.022$ |
| $\text{RFF},D=10$ | $0.270$ |
| $\text{RFF},D=100$ | $0.663$ |
| $\text{RFF},D=1000$ | $0.682$ |
| $\text{RFF},D=10000$ | $0.682$ |
随着$D$的增加,回归器在测试集上的$R^2$也在增加,当$D$足够大时,RFF的性能甚至超过了普通RBF核的性能。
接下来是分析时间。先用理论分析,对于一个$N\times d$的数据集,计算高斯核函数矩阵:
\[k(\pmb x,\pmb y)=\exp(-\gamma\Vert\pmb x-\pmb y\Vert_2^2)\]需要计算$N^2$次上式,每次计算需要求$d$维向量的内积,再计算指数幂,因此时间复杂度为$O(N^2d)$;而计算RFF时,我们要算
- 数据集矩阵$X_{N\times d}$与投影矩阵$W_{D\times d}$相乘,时间复杂度$O(NDd)$;
- 利用广播算法为上面的结果加上$b$,时间复杂度$O(ND)$;
- 广播$\cos$运算,时间复杂度$O(ND)$;
- 核矩阵计算,也就是计算$Z_{N\times D}Z_{N\times D}^T$,时间复杂度$O(N^2D)$.
因此,训练过程的时间复杂度是$O(N^2D+NDd)$,也就是说,对于很大的$N$或者$D$,计算往往十分耗时。虽然从理论上看,RFF似乎比普通RBF耗时;但RBF在计算指数函数时消耗了大量时间,这也是RBF核耗时的原因。所以我们需要从依靠实验观察。
from time import time
import numpy as np
import matplotlib.pyplot as plt
from rff import RFF
def calculate_rbf_time(N, d, gamma=1):
X = np.random.normal(size=(N, d))
t = time()
K = np.exp(-gamma * ((X**2).sum(1).reshape(-1, 1) + (X**2).sum(1) - 2 * X @ X.T))
ret = time() - t
return ret
def calculate_rff_time(N, d, D, gamma=1):
X = np.random.normal(size=(N, d))
t = time()
rff = RFF(D)
rff.fit(X)
Z = rff.transform(X)
K = Z @ Z.T
ret = time() - t
return ret
根据上面的性能测试,我们限制了抽样次数$D=1000$,对于不同的样本量$N$的数据,分别求RBF核和RFF核所需要时间:
n = 10000
rbf_list = [calculate_rbf_time(N, 10) for N in range(100, n + 1, 100)]
rff_list = [calculate_rff_time(N, 10, 1000) for N in range(100, n + 1, 100)]
plt.plot(range(100, n + 1, 100), rbf_list, label="rbf")
plt.plot(range(100, n + 1, 100), rff_list, label="rff")
plt.legend()
plt.show()
得到下图:
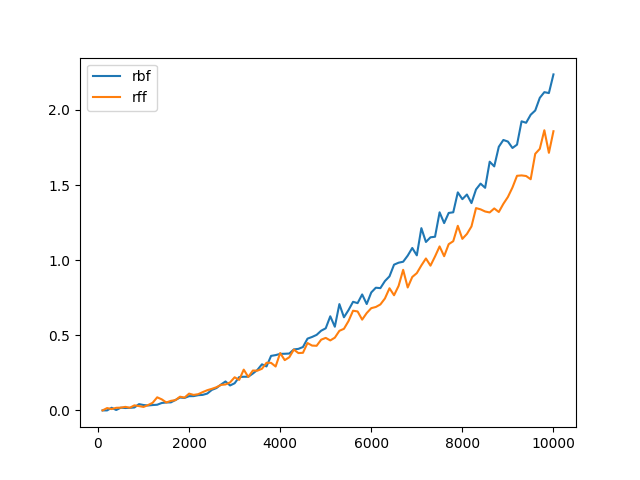
图像验证了计算时间确实是关于$N$的二次函数,此外,我们注意到当数据量越大,RFF相比于RBF有更大的速度提升。