引言
我们在之前提到利用numpy的广播算法来实现核函数的快速计算。而对于高斯核
我们会将中间二范数的平方拆开
\[\Vert\pmb{x}-\pmb{y}\Vert_2^2=\pmb{x}^T\pmb{x}+\pmb{y}^T\pmb{y}-2\pmb x^T\pmb y\]这已经比线性核多了几倍的运算量,再加上指数运算,对于大型数据集(十几万),是很耗时的。因此,Ali Rahimi和Benjamin Recht与2007年在《Random Features for Large-Scale Kernel Machines》提出随机傅里叶特征方法(RFF)来快速近似计算核函数。
思路
对于一对数据$\pmb x,\pmb y$,核函数$\phi(\mathbb{R}^d\to\mathbb{R}^\infty)$将它们映射到甚高维空间,然后计算它们的内积作为核函数的值:
\[k(\pmb x,\pmb y)=\phi(\pmb x)^T\phi(\pmb y)\]而RFF方法是选用一个映射$z(\mathbb{R}^d\to\mathbb{R}^D)$将数据映射到一个低维空间,但这里的“低”只是相对于$\phi$映射值域的无穷维来说的,$D$相比于$d$还是更大。然后将映射后的向量的内积作为核函数值的近似:
\[k(\pmb x,\pmb y)\approx z(\pmb x)^Tz(\pmb y)\]推导
首先明确,RFF主要是针对移位不变核:
\[k(\pmb x,\pmb y)=k(\pmb x-\pmb y)\]常见的移位不变核有高斯核,拉普拉斯核和柯西核,核函数分别是:
\[\begin{aligned} k_{\text{Gaussian}}(\Delta)&=\exp(-\frac{\Vert\Delta\Vert_2^2}{2})\\ k_{\text{Laplacian}}(\Delta)&=\exp(-\Vert\Delta\Vert_1)\\ k_{\text{Cauchy}}(\Delta)&=\prod_d(\frac{2}{1+\Delta_d^2}) \end{aligned}\]然后对移位不变核函数进行傅里叶逆变换:
\[\begin{aligned} k(\pmb x-\pmb y)&=\int_{\mathbb{R}^d}p(\pmb w)e^{j\pmb w^T(\pmb x-\pmb y)}\mathrm d\pmb w&(1)\\ &=\textbf{E}_{\pmb w}[e^{j\pmb w^T(\pmb x-\pmb y)}]&(2)\\ &=\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y))]&(3)\\ &=\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y)+2b)]+\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y))]&(4)\\ &=\textbf{E}_{\pmb w}[\sqrt 2\cos(\pmb w^T\pmb x+b)\sqrt 2\cos(\pmb w^T\pmb y+b)]&(5)\\ &=\textbf{E}_{\pmb w}[z_{\pmb w}(\pmb x) z_{\pmb w}(\pmb y)]&(6)\\ &=\dfrac1D\sum_{m=1}^Dz_{\pmb w_m}(\pmb x)z_{\pmb w_m}(\pmb y)&(7)\\ &=z(\pmb x)^Tz(\pmb y)&(8) \end{aligned}\]其中映射$z_{\pmb w}:\mathbb{R}^d\to\mathbb{R}$:
\[\begin{aligned} \pmb w&\sim p(\pmb w)\\ b&\sim\text{Uniform}(0,2\pi)\\ z_{\pmb w}(\pmb x)&=\sqrt2\cos(\pmb w^T\pmb x+b)\\ \end{aligned}\]我们现在证明上述一系列等式:
(1) 傅里叶逆变换。逆变换的标准式是
\[x(t)=\dfrac{1}{2\pi}\int_{-\infty}^\infty X(j\omega)e^{j\omega t}\mathrm d\omega\]这里将其推广到$\mathbb{R}^d$,同时将常数$\frac{1}{2\pi}$并进积分内。
(2) 我们可以认为$p(\pmb w)$是关于$\pmb w$的一个分布(详见Bochner定理),然后在有
\[\int p(\pmb w)f(\pmb w)\mathrm d\pmb w=\textbf{E}_{\pmb w}[f(\pmb w)]\]就可以将积分转为期望。前面三种移位不变核对应的$p(\pmb w)$:
| 核函数 | $k(\Delta)$ | $p(w)$ |
|---|---|---|
| 高斯核 | $\exp(-\frac{\Vert\Delta\Vert_2^2}{2})$ | $(2\pi)^{-\frac{D}{2}}\exp(-\frac{\Vert w\Vert_2^2}{2})$ |
| 拉普拉斯核 | $\exp(-\Vert\Delta\Vert_1)$ | $\prod_d\dfrac{1}{\pi(1+w_d^2)}$ |
| 柯西核 | $\prod_d\dfrac{2}{\pi(1+\Delta^2)}$ | $\exp(-\Vert\Delta\Vert_1)$ |
(3) 由于涉及的都是实值函数,欧拉公式变换下只有$\cos$项。
(4) 因为
\[\textbf{E}_{\pmb w}[\cos(\pmb w^T(\pmb x-\pmb y)+2b)]=\textbf{E}_{\pmb w}[\textbf{E}_{b}[\cos(\pmb w^T(\pmb x-\pmb y)+2b)\vert\pmb w]]\]令$t=\pmb w^T(\pmb x-\pmb y),x=2b$,则
\[\begin{aligned} \textbf{E}_{b}[\cos(\pmb w^T(\pmb x-\pmb y)+2b)\vert\pmb w]&=\int_{-\infty}^\infty p(x)\cos(t+x)\mathrm dx\\ &=\int_0^{4\pi}\dfrac{1}{4\pi}\cos(t+x)\mathrm dx\\ &=0 \end{aligned}\]所以整体的期望就是0。
(5) 和差化积公式。
(6) 定义映射$z_{\pmb w}$。
(7) 蒙特卡洛方法:抽样$D$次取均值,逼近期望。
(8) 可以将抽样求和拆解为两个向量的内积,得到映射$z$:
\[z(\pmb x)=\begin{bmatrix} \frac{1}{\sqrt D}z_{\pmb w_1(\pmb x)}\\ \frac{1}{\sqrt D}z_{\pmb w_2(\pmb x)}\\ \cdots\\ \frac{1}{\sqrt D}z_{\pmb w_D(\pmb x)}\\ \end{bmatrix}\]由此我们得到了一个低维显式随机投影$z$.
实验
我们利用sklearn数据集,利用FRR方法去计算核函数,并与标准核函数进行比较:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import *
from math import sqrt
# 标准的高斯核函数
std_gaussian = lambda x, y: np.exp(-((x**2).sum(1).reshape(-1, 1) +
(y**2).sum(1) - 2 * x @ y.T))
# 取鸢尾花数据集
X = load_iris().data
X = (X - X.mean(0)) / (X.std(0) + 1e-8)
d = X.shape[1] # 数据原维数
D = 10000 # 采样数,也就是映射z的投影维数
K1 = std_gaussian(X, X)
# 现在进行高斯核的FRR算法
b = np.random.uniform(0, 2 * np.pi, D)
w = np.random.multivariate_normal(np.zeros(d), np.eye(d), size=D)
Z = np.cos(X @ w.T + b) * sqrt(2 / D)
K2 = Z @ Z.T
选取第一行的元素进行比较:
plt.plot(K1[0][1:], label="std_kernel")
plt.plot(K2[0][1:], label="rff_kernel")
plt.legend()
plt.show()
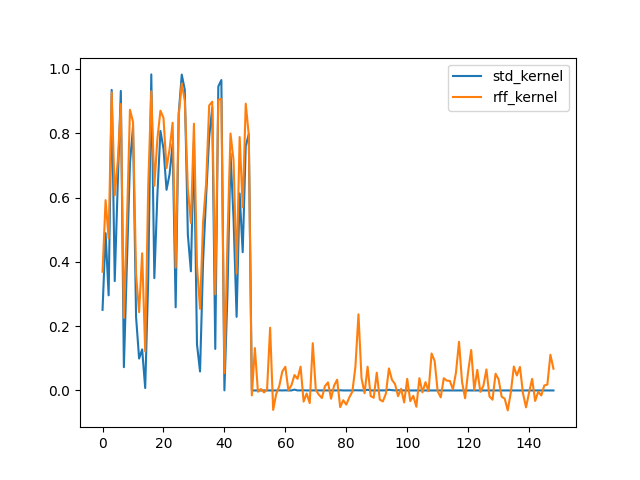
可以发现RFF方法能够较好的近似真实的高斯核函数。接着观察全局,可以绘制热力图:
sns.heatmap(K1)
plt.show()
sns.heatmap(K2, vmin=0, vmax=1)
plt.show()
标准的高斯核函数下的热力图:
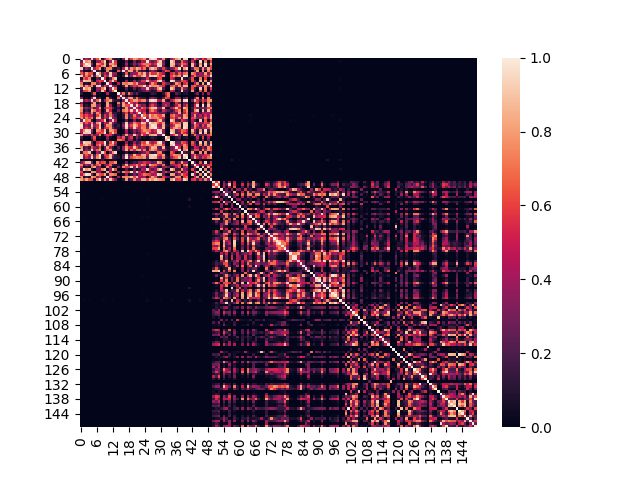
RFF方法下估计的核函数值热力图:
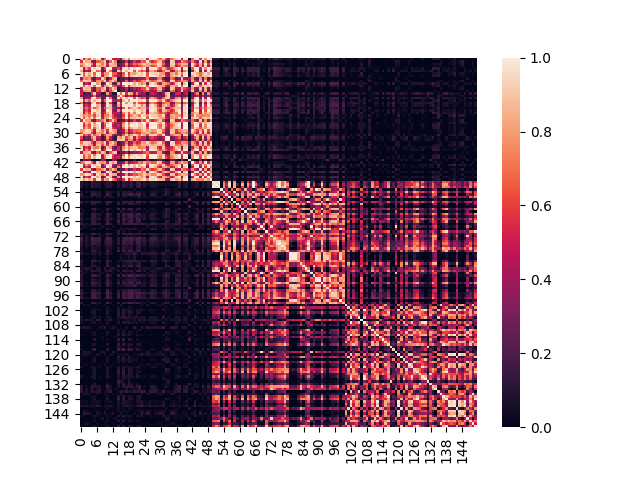
可以发现近似效果很好。
总结
我们详细推导了随机傅里叶特征法在核函数求解上的应用,并且通过可视化对近似核函数效果进行了验证。