引言
如果想对下面的数据集
进行回归,线性回归是一个很好的选择。当然,这样的数据往往只存在于理论中,真实世界的数据往往它复杂得多,比如这样的数据集:
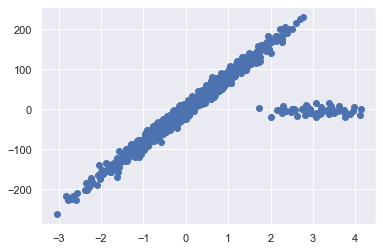
数据集中出现了离群点(outliers),如果我们仍使用线性模型,预测结果则会出现偏差:
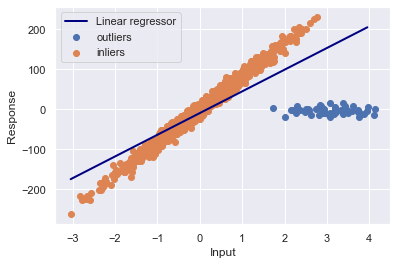
因此,我们需要一种回归模型,它能够识别出离群点并忽视它们进行回归。这种回归模型就是鲁棒回归(Robust regression。在统计学领域和机器学习领域,对异常值也能保持稳定、可靠的性质,称为鲁棒性。我们这里介绍两种鲁棒回归模型的工作原理和实现。
Huber回归
线性回归的核心是最小二乘法,也就是优化
\[\min_{w}\sum_{i=1}^n(wx_i-y_i)^2\]但优化
\[\min_{w}\sum_{i=1}^n\vert wx-y\vert\]更直观,且意义更明确,也就是最小化目标值和预测值间的距离,这叫做“最小一乘法”。绝对值函数带来的不可微特性使得最小一乘不如最小二乘易于求解,但这并不代表最小一乘在性能上不如最小二乘。事实上,最小一乘可以得到相比于最小二乘更鲁棒的参数解。
所谓的鲁棒性,也就是对异常值不敏感,对于一个异常值$(\bar{x}_i,\bar{y}_i)$,也就是距离
\[\vert w\bar{x}_i-\bar{y}_i\vert\]很大,在最小二乘中,二次函数将其损失放大(相比于绝对值函数),使得参数优化时向该异常样本大幅度倾斜,也就是对异常值敏感。这是笔者认为最小二乘不如最小一乘鲁棒的原因。
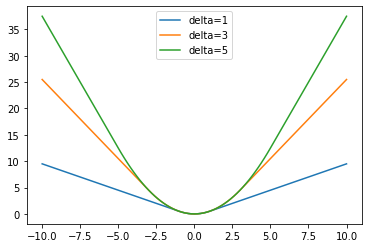
我们在前面提到,最小一乘的一个缺陷就是其在零点处不可微,这就是Huber回归出场的时候。Huber回归采用的损失函数为用二次函数平滑的绝对值函数:
\[f_\delta(x)=\begin{cases} \frac12x^2&\vert x\vert\leq\delta\\ \delta x-\frac12\delta^2&\vert x\vert>\delta \end{cases}\]对于不同的参数$\delta$,我们可以得到不同的Huber损失函数:
由此,Huber回归的优化问题:
\[\min_{w}\sum_{i=1}^{n}\text{huber}_\delta(wx_i-y_i)\]我们可以用梯度下降法求解该问题,代码地址:HuberRegressor.
对引言中的数据使用Huber回归,并与线性回归效果进行比较并可视化:
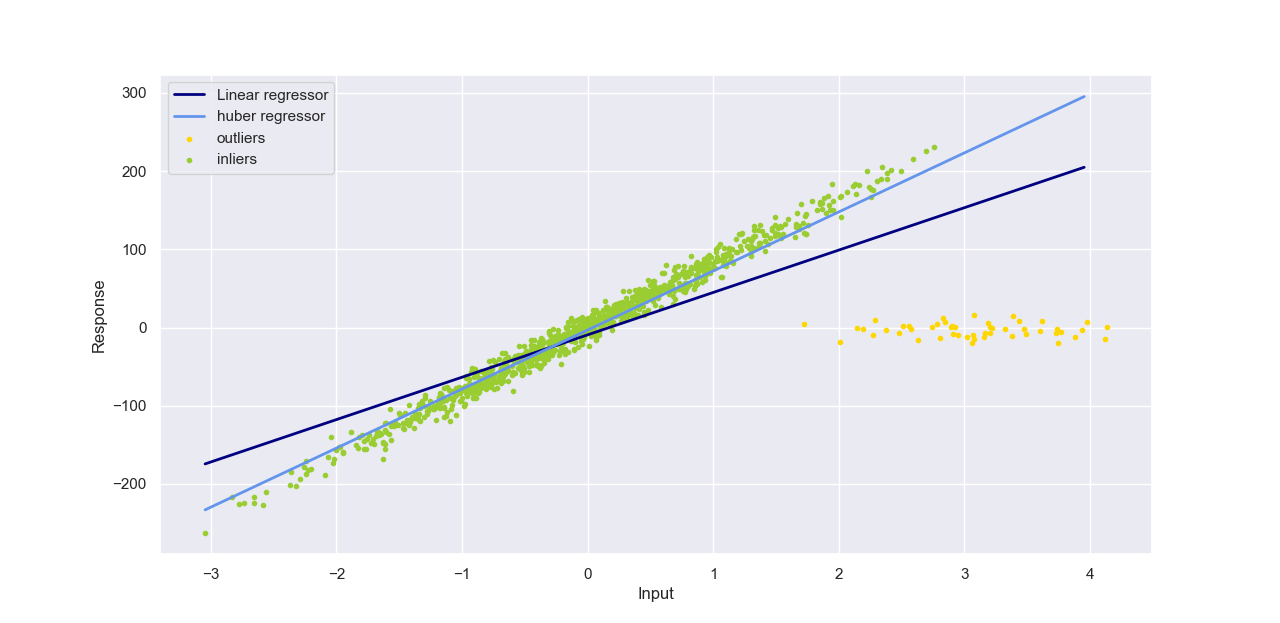
可以发现Huber回归结果更鲁棒,也就是对异常值不敏感。
RANSAC
从上图中可以看出,Huber回归的结果对异常点仍然有一定的偏向,是否有一种回归算法,能够判断出离群点,从而可以舍弃这些数据,再计算回归参数?
随机抽样一致算法(RANdom Sample Consensus, RANSAC),采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。算法的过程不难:
- 对于一个$n$特征训练数据集,我们随机抽取$n$个数据点,用线性回归法拟合出一个回归方程;
- 用该方程去预测训练集中的样本,将误差未超过设定阈值$\sigma$的样本点标记为未离群点(inliers);
- 找到能使未离群点数最大的回归方程,当最大未离群点数超过总样本数的1/2时,便停止迭代,返回其对应的回归方程参数,否则继续迭代。
该算法也常被用于图像处理。我们也不难写出算法:
pretotal = 0
max_iter = 1000
sigma = 0.5
for i in range(max_iter):
# 选取样本,样本数为自变量维数
sample_index = np.random.choice(l, X.shape[1])
sample_X, sample_y = X[sample_index], y[sample_index]
# 线性回归问题解析解w = (X^T X) X^T y
big_X = sample_X.T @ sample_X
if np.linalg.matrix_rank(big_X) < big_X.shape[0]:
# 在多维数据下,防止对奇异矩阵求逆,从而加上单位矩阵
big_X += 1e-3 * np.eye(big_X.shape[0])
coef = np.linalg.inv(big_X) @ sample_X.T @ sample_y
# 计算非离群点
total_inlier = np.sum(np.abs(X @ coef - y) < sigma)
if total_inlier > pretotal:
pretotal = total_inlier
best_coef = coef
# 迭代终止条件
if total_inlier > 0.5 * l:
break
# best_coe就是我们的目标参数
和前面类似,我们将RANSAC和线性回归的结果可视化以进行比较:
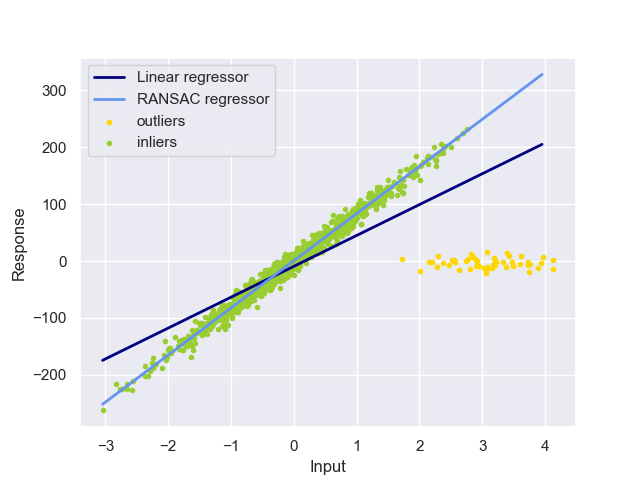
可以发现,RANSAC算法具有很好的鲁棒性,成功对非离群点进行很好的拟合。