引入
One Class SVM属于无监督的SVM算法,被用于对数据集中的异常点进行检测(也叫分布估计)。异常数据对机器学习效果有非常消极的影响,比如下面的人造数据分布:
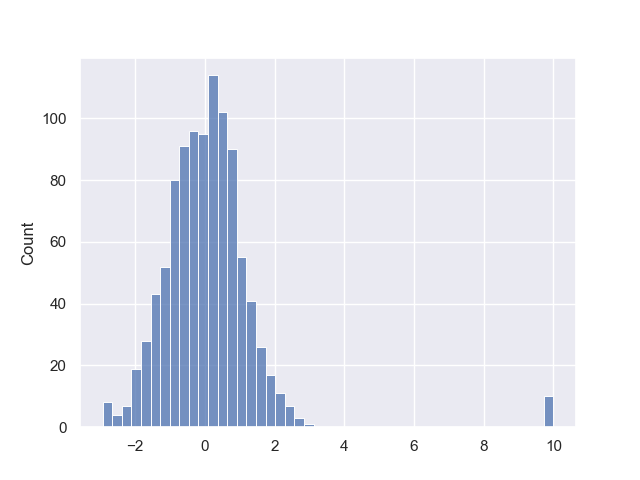
该数据集是从$\mathcal{N}(0,1)$分布中取990个样本,然后混杂10个从$\mathcal{N}(10,0.001)$的样本,那么这10个样本就属于异常点。我们无法通过标准化、归一化等预处理方法去剔除。
一种最简单的异常检测,就是通过正态分布的3$\sigma$原则去判定:去除所有不在区间$(\mu-3\sigma,\mu+3\sigma)$内的数据。但这种方法对数据分布有很高的要求(正态分布),因此我们需要其他的异常检测算法。One Class SVM正是面向该问题提出,其基本思想是,用SVM训练一个超平面:
\[f(\pmb x)=\sum_{i=1}^n\pmb \alpha_iK(\pmb x_i,\pmb x)+b=0\]用
\[\text{sgn}\bigg(\sum_{i=1}^n\pmb \alpha_iK(\pmb x_i,\pmb x)+b\bigg)\]作为决策函数,如果决策函数的值为1,则判定为属于该数据分布;函数值为-1则判定为离群点。
问题求解
one-class SVM优化问题的形式:给定无类别数据$X=[\pmb x_1,\pmb x_2,\cdots,\pmb x_l]$,我们要优化
\[\begin{aligned} \min\quad&\frac12\pmb w^T\pmb w-\rho+\dfrac{1}{\nu l}\sum_{i=1}^l\xi_i\\ \text{s.t.}\quad&\pmb w^T\phi(\pmb x_i)\geq\rho-\xi_i,\\ &\xi_i\geq0,i=1,\cdots,l \end{aligned}\]其对偶问题为
\[\begin{aligned} \min_{\pmb\alpha}\quad&\frac12\pmb\alpha^TQ\pmb\alpha\\ \text{s.t.}\quad&0\leq\alpha_i\leq1/(\nu l),i=1,\cdots,l\\ &\pmb e^T\pmb\alpha=1 \end{aligned}\]其中$Q_{ij}=K(\pmb x_i,\pmb x_j)$,这是一个但线性约束下的二次规划问题,可以用SMO算法求解,解出来后得到决策函数(也就是上面提到的决策函数)
\[\text{sgn}\bigg(\sum_{i=1}^l\alpha_iK(\pmb x_i,\pmb x)-\rho\bigg)\]注意到$\alpha_i$要控制在$[0,1/(\nu l)]$之内,当数据量,也就是$l$很大时,是不利于$\pmb\alpha$的迭代求解的。因此,在libsvm中求解的其实是对偶问题的一个放缩版本:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\frac12\pmb\alpha^TQ\pmb\alpha\\ \text{s.t.}\quad&0\leq\alpha_i\leq1,i=1,\cdots,l\\ &\pmb e^T\pmb\alpha=\nu l \end{aligned}\]这里将$\pmb\alpha$扩大了$\nu l$倍,而在https://welts.xyz/2021/09/25/mysvm/中,我们说明了$\rho$其实是优化函数$f(\pmb\alpha)$的梯度元素的线性组合:
\[\rho=\sum_{i=1}^l k_i\nabla_i f(\pmb\alpha)=\frac12\sum_{i=1}^lk_iQ_i^T\pmb\alpha\]如果$\pmb\alpha$扩大了$\nu l$倍,$\rho$会扩大相同的倍数,从而
\[\sum_{i=1}^l\alpha_iK(\pmb x_i,\pmb x)-\rho=0\equiv\sum_{i=1}^l\nu l\alpha_iK(\pmb x_i,\pmb x)-\nu l\rho=0\]形成的超平面是相同的,从而证明了两个对偶问题是等价的。
自实现和效果验证
我们在https://github.com/Kaslanarian/PythonSVM/blob/main/one_class.py中实现了One-class SVM,现在用我们自己实现的模型对上面的数据进行验证:
import matplotlib.pyplot as plt
import numpy as np
from one_class import OneClassSVM # 调用我们自己设计的模型
import seaborn as sns
X_train = np.random.randn(1000)
X_train[:10] = 0.001 * np.random.randn(10) + 10
model = OneClassSVM(nu=0.1)
model.fit(X_train.reshape(-1, 1))
X_test = np.linspace(-4, 16, 101)
pred = model.decision_function(X_test.reshape(-1, 1))
plt.plot(X_test, pred)
plt.show()
我们绘制出输入-决策函数值曲线:
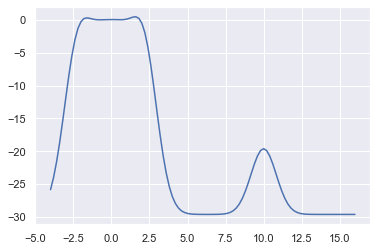
可以看到决策函数很好拟合了前面的数据分布。此外,决策函数值为负的点判定为离群点,从上面的图像来看,参数$\nu=0.1$训练出的模型过于严苛,只有很小一部分点不被排除,损失了大量数据,而且边界不显著。
我们将$\nu$设为0.9:
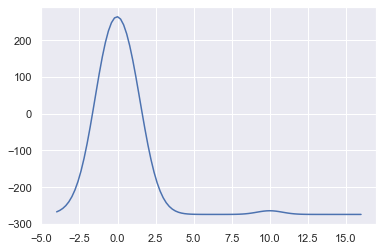
这样,决策边界比较显著,同时拟合结果更符合训练数据。
我们再用一个sklearn文档中的例子,它是将100个正常数据(二维正态分布)和20个异常数据(均匀分布)用OneClassSVM训练,绘制异常区域的轮廓,把异常区域划分为7个层次:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn import svm
from one_class import OneClassSVM
# 背景坐标点阵
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# 生成训练数据
X = 0.3 * np.random.randn(100, 2) # 100个正常数据,shape=(100,2),[0,1)之间
X_train = np.r_[X + 2, X - 2] # 向左侧平移2得到一组数据,向右侧平移2得到一组数据,两组数据串联,
# 生成测试数据
X = 0.3 * np.random.randn(20, 2) # 20个异常数据
X_test = np.r_[X + 2, X - 2] # 向左侧平移2得到一组数据,向右侧平移2得到一组数据,两组数据串联,
# 生成20个异常数据,
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
# 训练模型
# clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1) # 调用的是sklearn中的SVM
clf = OneClassSVM(nu=0.1, kernel='rbf', gamma=0.1)
clf.fit(X_train)
#----》判断数据是在超平面内还是超平面外,返回+1或-1,正号是超平面内,负号是在超平面外
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
# 统计预测错误的个数
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size
# 计算网格数据到超平面的距离,含正负号
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) # ravel表示数组拉直
Z = Z.reshape(xx.shape)
"""
绘图
"""
plt.title("Novelty Detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7),
cmap=plt.cm.PuBu) #绘制异常区域的轮廓, 把异常区域划分为7个层次
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2,
colors='darkred') # 绘制轮廓,SVM的边界点(到边界距离为0的点
plt.contourf(xx, yy, Z, levels=[0, Z.max()],
colors='palevioletred') # 绘制正常样本的区域,使用带有填充的轮廓
s = 40 # 样本点的尺寸大小
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s,
edgecolors='k') # 绘制训练样本,填充白色,边缘”k“色
b2 = plt.scatter(X_test[:, 0],
X_test[:, 1],
c='blueviolet',
s=s,
edgecolors='k') # 绘制测试样本--正常样本,填充蓝色,边缘”k“色
c = plt.scatter(X_outliers[:, 0],
X_outliers[:, 1],
c='gold',
s=s,
edgecolors='k') # 绘制测试样本--异常样本,填充金色,边缘”k“色
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
# 集中添加图注
plt.legend([a.collections[0], b1, b2, c], [
"learned frontier", "training data", "test regular data",
"test abnormal data"
],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlabel(
"error train: %d/200 ; errors novel regular: %d/40 ; errors novel abnormal: %d/40"
% (n_error_train, n_error_test, n_error_outliers))
plt.show()
分别调用sklearn中的和自设计的OneClassSVM,观察效果差别:
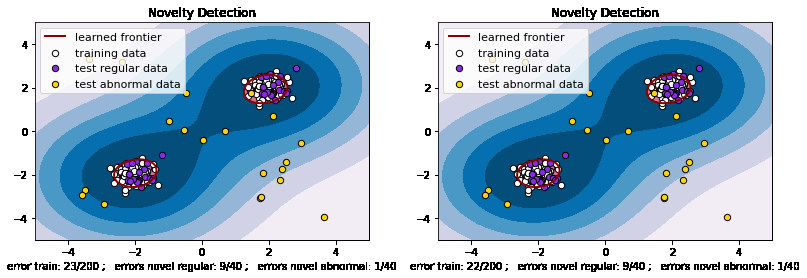
左边是sklearn模型,右边是我们设计的模型,可以发现两者训练结果差别不大,说明我们的实现是正确的。
总结
我们实现了OneClassSVM模型,它拥有和sklearn中的OneClassSVM相近的能力,可以胜任不少异常检测任务。