引言
在大致读完libsvm源码后,我们就可以尝试实现自己的支持向量机。在Kaslanarian/PythonSVM: 支持向量机模型(分类与回归)的Python(numpy)实现 (github.com)中,我们自实现了SMO优化算法,并实现了libsvm中提到的五种支持向量机。
SMO算法的实现
基础SMO
在支持向量分类($C$-SVC)和支持向量回归($\varepsilon$-SVR)中,我们要求解的对偶问题满足下面的形式:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^TQ\pmb\alpha+\pmb p^T\pmb\alpha\\ \text{s.t.}\quad&\pmb y^T\pmb\alpha=\delta,y_i\in\{-1,+1\}\\ &0\leq\alpha_i\leq C \end{aligned}\]由此,我们可以写出一个求解上述问题的类:
class Solver:
'''
Parameters
----------
l : 向量长度
Q : 待优化函数的二次项
p : 待优化函数的一次项
y : 限制条件中的y向量
Cp: 正样本的限制C
Cn: 负样本的限制C
tol: 容忍度
max_iter: 最大迭代次数
'''
def __init__(l, Q, p, y, Cp, Cn, tol, max_iter):
'''初始化构造函数'''
pass
def solve(self):
'''求解'''
pass
def select_working_set(self):
'''工作集选取'''
pass
def update(self, i, j):
'''对指定的工作集进行更新,剪辑等操作'''
pass
def calculate_rho(self):
'''
计算参数rho(ρ),
在C-SVC, ε-SVR和One-class-SVM中
ρ + b = 0
'''
pass
def get_alpha(self):
'''获取参数α'''
return self.alpha
def get_rho(self):
'''获取参数ρ'''
return self.rho
def get_b(self):
'''获取参数b'''
return self.b
Solver类的solve方法遵循下面的算法:
process SMO() {
for i<-1 to max_iter {
i, j <- select_working_set() /* 选择工作集 */
update(i, j) /* 更新一次 */
if coverage then break /* 如果收敛就不需继续迭代 */
}
calculate_rho() /* 计算偏移参数 */
}
其中工作集的选取和更新已经在https://welts.xyz/2021/07/10/wss/和https://welts.xyz/2021/07/11/libsmo/中提及,这里主要来研究参数$\rho$和$b$的计算。在周志华老师的《机器学习》中提到了计算偏移量$b$的启发式方法,也就是将所有符合条件的支持向量对应的$b$去均值,其中$\text{nSV}$为支持向量的个数:
\[\begin{aligned} b&=\dfrac{1}{\text{nSV}}\sum_{i=1}^{\text{nSV}}\bigg(y_i-\sum_{j=1}^n\alpha_jy_jx_j^Tx_i\bigg)\\ &=\dfrac{1}{\text{nSV}}\sum_{i=1}^{\text{nSV}}-y_i\nabla f_i(\alpha)\\ &=-\dfrac{\sum_{i:0<\alpha_i<C}y_i\nabla_if(\alpha)}{\vert\{i\vert0<\alpha_i<C\} \vert}\\ &=-\rho \end{aligned}\]现在问题来了,如果不存在满足$0<\alpha_i<C$的$\alpha_i$呢,我们需要另做处理:令
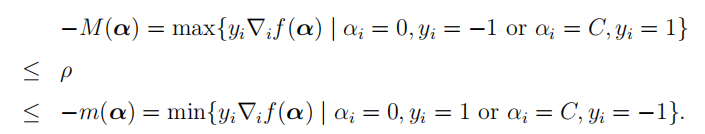
让$\rho$取上下界的均值。
NuSVM下的SMO
$\nu$-SVC和$\nu$-SVR下的SMO问题要比前面的复杂,体现在多出一个线性约束:
\(\begin{aligned}
\min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^TQ\pmb\alpha+\pmb p^T\pmb\alpha\\
\text{s.t.}\quad&\pmb{y}^T\pmb\alpha=\delta_1,y_i\in\{-1,+1\}\\
&\pmb e^T\pmb\alpha=\delta_2,\\
&0\leq\alpha_i\leq C
\end{aligned}\)
其中$\pmb e$为全1向量。那么,如果我们还是想原来那样选择工作集(working_set_select),假设选择一对$i,j$满足
\(y_i\neq y_j\)
那么根据约束条件,在更新时必须满足两个不等式:
\(\begin{cases}
\alpha_i+\alpha_j=C_1\\
\alpha_i-\alpha_j=C_2\\
\end{cases}\)
也就是$\alpha_i,\alpha_j$要同时在两条直线上:
可行域只有一个交点,结果便是无法更新。因此,$\nu$-SVM的在选取工作集时必须要满足 \(y_i=y_j\) 这样才能使约束缩减成一个,也就是$\alpha_i+\alpha_j=C_1$,因此在选择工作集时,我们分别从满足$y_i=+1$的$\alpha_i$中用原来的方法选出一对候选工作集$i_p,j_p$,类似的,再从满足$y_i=-1$的$\alpha_i$中选出一对$i_n,j_n$,最后返回哪一对取决于谁可以让目标值有更大的下降。
由此,我们可以写出求解该类问题的类NuSolver:
class NuSolver(Solver):
pass # 成员函数名和基类相同
其继承了前面的Solver类。值得注意的是,NuSolver中$b$和$\rho$的计算和Solver存在差异,这是由KKT条件的不同导致的,我们只介绍怎么做:先求
然后解
\[\begin{cases} \rho-b=r_1\\ \rho+b=r_2\\ \end{cases}\]就可求出$\rho$和$b$。如果在求$r_1,r_2$时不存在这样的支持向量,则和上面一样取上下界的均值,只不过要加上$y_i$的限制,比如$r_1$的上下界:
\[\max_{\alpha_i=C,y_i=1}\nabla_if(\pmb\alpha)\leq r_1\leq\min_{\alpha_i=0,y_i=1}\nabla_if(\pmb\alpha)\]由此我们可以求解上述的两种线性等式约束下的二次规划问题。