高阶张量与Pytorch

引言

在Numpy与数据结构 - 邢存远的博客 Welt Xing’s Blog (welts.xyz)中，我们讨论了numpy的向量和矩阵的五则运算，并在研究更高维数据结构前停了下来，因为当时的工作并不会涉及到它。

我们现在来看sklearn模块中的digits数据集，这是将8*8的数字图片展平成长度为64的向量的数据集：

from sklearn.datasets import load_digits
import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape) # 输出(1797, 64)
x = X[0]
plt.imshow(x.reshape(8, 8), cmap="gray")
plt.show()

第一条数据变换形状后如下：

zero

因此，原数据集应该是

X_origin = X.reshape(1797, 8, 8)

也就是1797张图片，这是在CV任务中常见的数据格式，这样的numpy数据结构的维度超越了向量和矩阵，而是三阶张量。

张量简介

张量（Tensor）本身是数学名词。在力学中有重要应用。张量这一术语起源于力学，它最初是用来表示弹性介质中各点应力状态的，后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要，在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广，矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。

但在机器学习/深度学习领域中，张量其实等于多维数组，比如：

\[\begin{bmatrix} 1 \end{bmatrix},\begin{bmatrix} 1\\2 \end{bmatrix},\begin{bmatrix} 1&2\\ 3&4\\ \end{bmatrix}\]

分别是实数、向量和矩阵，用张量的术语来说，就是零阶、一阶和二阶张量。一个以矩阵为元素的向量，就是三阶张量：

\[\begin{bmatrix} \begin{bmatrix} 1&2\\ 3&4\\ \end{bmatrix},\\\begin{bmatrix} 5&6\\ 7&8\\ \end{bmatrix} \end{bmatrix}\]

三阶张量可以用一个立方体表示，比如上面的数据，就是长宽高为2的正方体。我们在Pillow - 邢存远的博客 Welt Xing’s Blog (welts.xyz)中研究的RGB图片，也是三维张量：长和高是图片的长和高，宽是图片的通道数，比如jpg格式下的通道数就是3，png的通道数是4.

至于四阶张量，就是一个以三阶张量（立方体）为元素的向量，五阶张量是以三阶张量为元素的矩阵。类似于三阶张量与彩色图片对应，四阶张量在现实中也有对应的模型，那就是彩色视频，视频是一个“向量”，其中每一个帧（元素）就是一张彩色图片，对应的就是一个立方体（三阶张量）。

下图是1-5阶张量的视图：

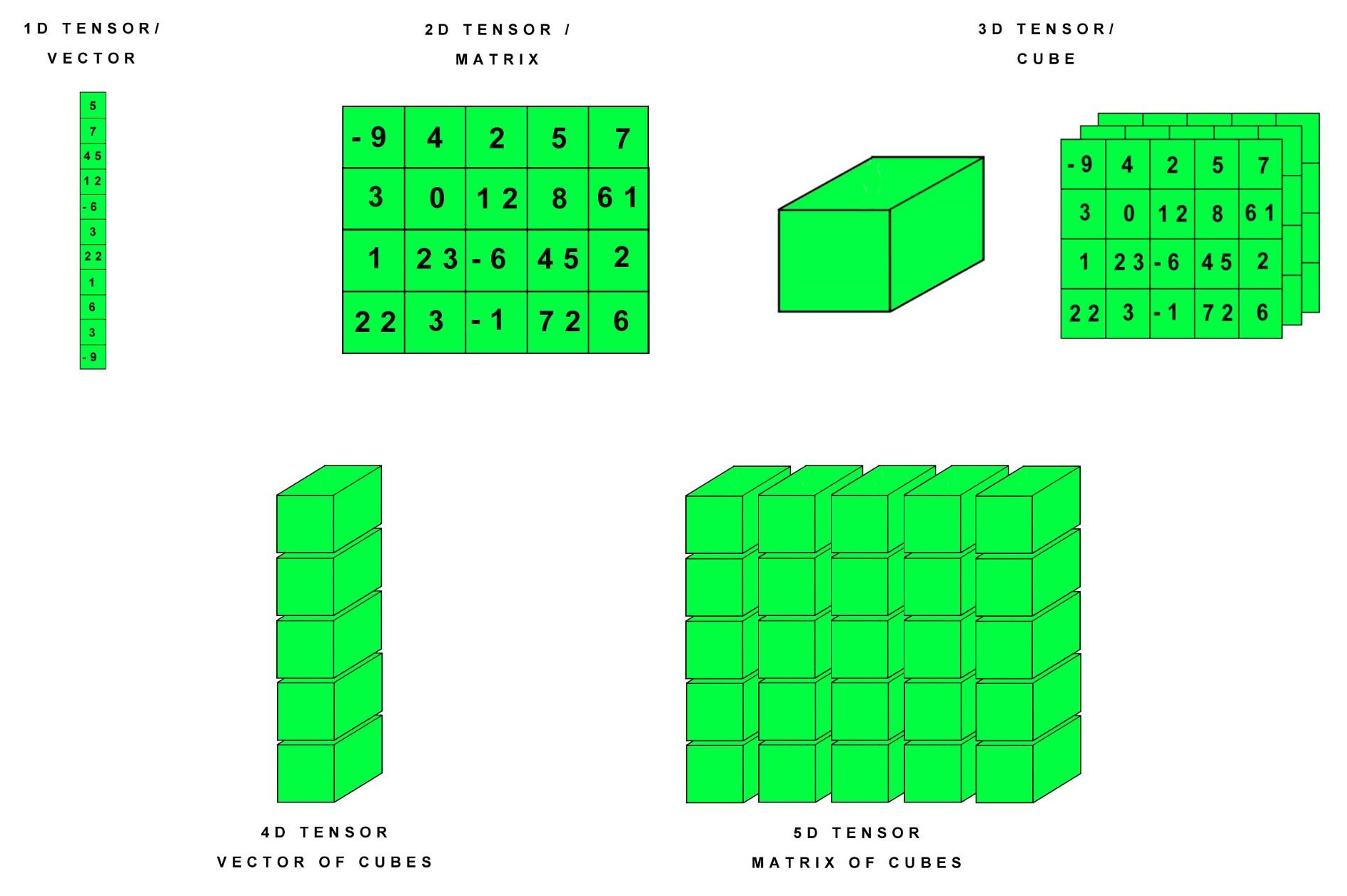
tensors

Tensor与array

我们想用torch来创建和计算张量，torch可以被看做的神经网络中的numpy，torch中tensor和numpy中的array有较强的兼容性，因此如果熟悉numpy的ndarray的使用，操作torch中的Tensor不会很难。

相互转换

import torch
import numpy as np

ndarray = np.random.randn(2, 3, 3) # 三阶张量
tensor = torch.from_numpy(ndarray) # numpy转torch
tensor2array = tensor.numpy()      # torch转numpy

print(ndarray, '\n')
print(tensor, '\n')

输出结果：

[[[-0.43864337  1.0760334   1.1875567 ]
  [ 1.6121431   0.77393113  2.57929563]
  [-0.08573594 -1.47966476  1.64749027]]

 [[-0.41425095 -1.5315761   1.09946891]
  [ 0.61153365  0.56446711  0.22129648]
  [ 0.27754899  0.72332455 -1.24759087]]]

tensor([[[-0.4386,  1.0760,  1.1876],
         [ 1.6121,  0.7739,  2.5793],
         [-0.0857, -1.4797,  1.6475]],

        [[-0.4143, -1.5316,  1.0995],
         [ 0.6115,  0.5645,  0.2213],
         [ 0.2775,  0.7233, -1.2476]]], dtype=torch.float64)

一个启发就是，我们不需要再花费大量时间去学torch中创建张量的语法，只需要用numpy创建再转成torch中的tensor即可。

此外，观察其输出，不难知道如何通过列表索引获取对应元素：

t = torch.randn(2, 3, 4)
t[0] # 3*4矩阵，两个3*4矩阵中的第一个
t[0, 1] # 等价于t[0][1]，是第一个矩阵的第二行
t[0, 1, 2] # 等价于t[0][1][2]，第一个矩阵的第二行的第三个元素

张量运算

torch中张量的运算和numpy兼容，向量和矩阵的乘法在之前已经讨论过了，我们这里主要研究三阶张量的运算规律。

广播四则运算

对于形状相同的张量：

t1 = torch.randn(2, 3, 4)
t2 = torch.randn(2, 3, 4)

print(t1 + t2)
print(t1 - t2)

输出的结果就是对应元素相加/相减。如果形状不同，则可能是广播加减法，比如：

t1 = torch.zeros((2, 3, 4)) # 全0张量
t2 = torch.randn(3, 4)

print(t2, '\n')
print(t1 + t2)

输出：

tensor([[-0.0456, -0.0922, -1.1588, -1.2053],
        [-0.0265,  0.2595, -2.2082, -0.0265],
        [ 0.0170, -0.1348, -0.4335, -0.6538]]) 

tensor([[[-0.0456, -0.0922, -1.1588, -1.2053],
         [-0.0265,  0.2595, -2.2082, -0.0265],
         [ 0.0170, -0.1348, -0.4335, -0.6538]],

        [[-0.0456, -0.0922, -1.1588, -1.2053],
         [-0.0265,  0.2595, -2.2082, -0.0265],
         [ 0.0170, -0.1348, -0.4335, -0.6538]]])

tensor[0]和tensor[1]元素相等，都是t1矩阵的值。

如何理解？将三阶张量$t$视作矩阵的数组（向量）。numpy和pytorch中，一个数组（向量）加上一个实数，结果就是将向量中的所有元素都加上这一实数。矩阵的数组加上一个矩阵$m$，那就是向量中的每个元素都加上这个矩阵。

这就要求$m$必须可以和$t[0]$相加，除了两者形状相等外（m.shape == t.shape[1:]），不要忘了矩阵和向量之间也可以进行广播加减法：

t1 = torch.zeros((2, 3, 4))
t2 = torch.randn(4) 
# 也可以是1*4矩阵，效果相同：torch.randn(1, 4)

print(t2, '\n')
print(t1 + t2)

输出

tensor([ 1.0410, -1.5886, -0.1257, -0.5639]) 

tensor([[[ 1.0410, -1.5886, -0.1257, -0.5639],
         [ 1.0410, -1.5886, -0.1257, -0.5639],
         [ 1.0410, -1.5886, -0.1257, -0.5639]],

        [[ 1.0410, -1.5886, -0.1257, -0.5639],
         [ 1.0410, -1.5886, -0.1257, -0.5639],
         [ 1.0410, -1.5886, -0.1257, -0.5639]]])

张量乘法

将高阶张量的后两个维度视作矩阵，然后执行矩阵乘法，就是张量乘法的核心。我们看最简单的：

t1 = torch.arange(2 * 2 * 3).view((2, 2, 3)) + 0. # "+0."进行类型转换
t2 = torch.ones(3)
t = t1 @ t2
print(t1, '\n')
print(t)

将(2,2,3)张量同长度为3的向量相乘，输出：

tensor([[[ 0.,  1.,  2.],
         [ 3.,  4.,  5.]],
        [[ 6.,  7.,  8.],
         [ 9., 10., 11.]]]) 

tensor([[ 3., 12.],
        [21., 30.]])

两个矩阵分别与全1向量相乘：

\[\begin{bmatrix} 0&1&2\\ 3&4&5 \end{bmatrix}\begin{bmatrix} 1\\1\\1\\ \end{bmatrix}=\begin{bmatrix} 3&12 \end{bmatrix}, \begin{bmatrix} 6&7&8\\ 9&10&11 \end{bmatrix}\begin{bmatrix} 1\\1\\1\\ \end{bmatrix}=\begin{bmatrix} 21&30 \end{bmatrix}\]

也就是结果t。进一步扩展，类似的，将三阶张量同单位矩阵相乘：

t1 = torch.arange(2 * 2 * 3).view((2, 2, 3)) + 0. # "+0."进行类型转换
t2 = torch.eye(3)
t = t1 @ t2
print(t1, '\n')
print(t)

输出：

tensor([[[ 0.,  1.,  2.],
         [ 3.,  4.,  5.]],
        [[ 6.,  7.,  8.],
         [ 9., 10., 11.]]]) 

tensor([[[ 0.,  1.,  2.],
         [ 3.,  4.,  5.]],
        [[ 6.,  7.,  8.],
         [ 9., 10., 11.]]])

还是三阶张量的两个矩阵同单位矩阵相乘：

\[\begin{bmatrix} 0&1&2\\ 3&4&5 \end{bmatrix}\begin{bmatrix} 1&&\\&1&\\&&1\\ \end{bmatrix}=\begin{bmatrix} 0&1&2\\ 3&4&5 \end{bmatrix}, \begin{bmatrix} 6&7&8\\ 9&10&11 \end{bmatrix}\begin{bmatrix} 1&&\\&1&\\&&1\\ \end{bmatrix}=\begin{bmatrix} 6&7&8\\ 9&10&11 \end{bmatrix}\]

然后拼接成结果t。

至于高阶张量之间的运算，规则是这样的：除去最后两个维度之外（最后两个维度满足矩阵乘法，即前一个矩阵的列数等于后一个矩阵的行数），剩下的维度按照上面提到的广播机制进行乘法运算。比如

t1 = torch.randn(2, 3, 4, 5)
t2 = torch.randn(3, 5, 2)
t = t1 @ t2

t1和t2最后两个维度分别是(4, 5)和(5, 2)，满足矩阵乘法，将一个矩阵视作是矩阵中的一个entry：

\[t_1=\begin{bmatrix} A_{11}&A_{12}&A_{13}\\ A_{21}&A_{22}&A_{23}\\ \end{bmatrix},t_2=\begin{bmatrix} B_{1}\\ B_{2}\\ B_{3}\\ \end{bmatrix}\]

每一个$A_{ij}$都是一个4*5矩阵，每一个$B_i$都是一个5*2矩阵，然后作广播乘法，得到：

\[t=\begin{bmatrix} A_{11}B_1&A_{12}B_2&A_{13}B_3\\ A_{21}B_1&A_{22}B_2&A_{23}B_3\\ \end{bmatrix}\]

每一个$A_{ij}B_j$都是一个4*2矩阵，从而t是一个形状为$(2,3,4,2)$的四阶张量：

print(t.shape)

输出

torch.Size([2, 3, 4, 2])

至此我们介绍完了张量的基本操作与运算，为后面的工作提供了帮助。

原理与运算

引言