引言
从本文开始笔者打算讨论卷积神经网络,和组里进度相匹配。卷积神经网络在过去的十年里,在与模式识别相关的各个领域都取得了突破性的结果;从图像处理到语音识别。其最有益的方面是减少人工神经网络中参数的数量。这一成就促使研究人员和开发人员都使用更大的模型来解决复杂的任务,而这对于经典的ANN是不可能的。关于CNN解决的问题,最重要的假设是不应该具有空间相关的特征。例如,在人脸检测应用程序中,我们不需要注意人脸在图像中的位置。唯一关心的是检测它们,而不管它们在给定的图像中的位置如何。CNN的另一个重要方面是,当输入向更深层传播时,要获得抽象的特征。例如,在图像分类中,边缘可以在第一层中检测到,然后在第二层中检测到更简单的形状,然后是更高级别的特征。
卷积
卷积的必要性
我们这里需要操作的jpg图片,比如:

满足下图的模型:
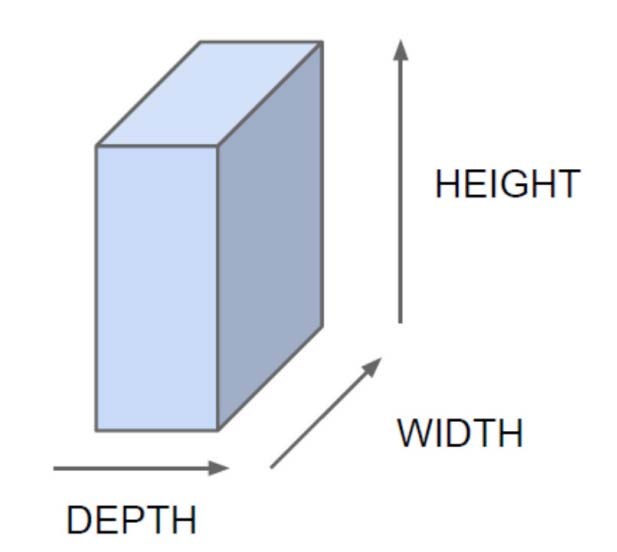
长608个像素,宽482像素,4通道的图片对应的height,width和depth就是608,482和4. 如果我们将该图片作为训练样本,即使是用一个单层感知机模型去进行二分类,也需要608*482*4+1=1172225 个参数,实在是太多。因此我们需要一种方法对图片进行压缩(池化),但要求压缩后图片的一个像素可以表征多个压缩前的像素(卷积)。卷积神经网络便是采用先卷积后池化的方式,先提取特征,再缩小参数数量,然后送入全连接网络进行学习。
卷积操作
下图是用一个3*3的卷积核对一个5*5图像去操作:
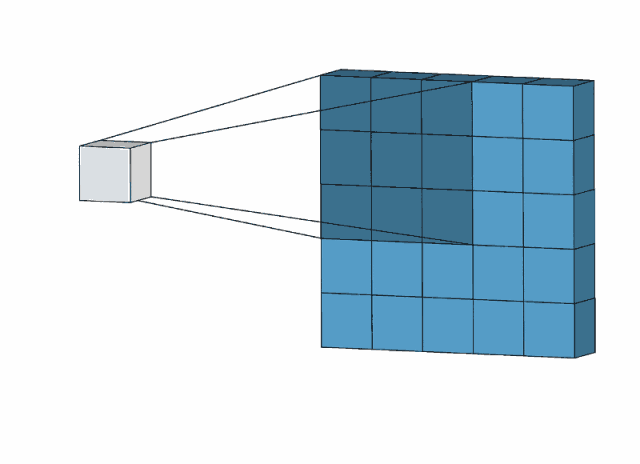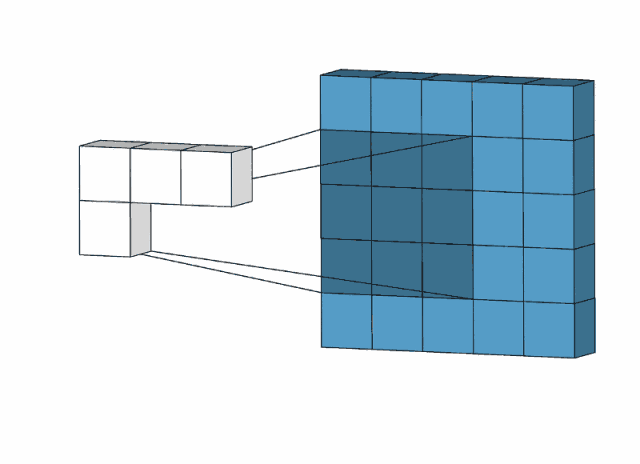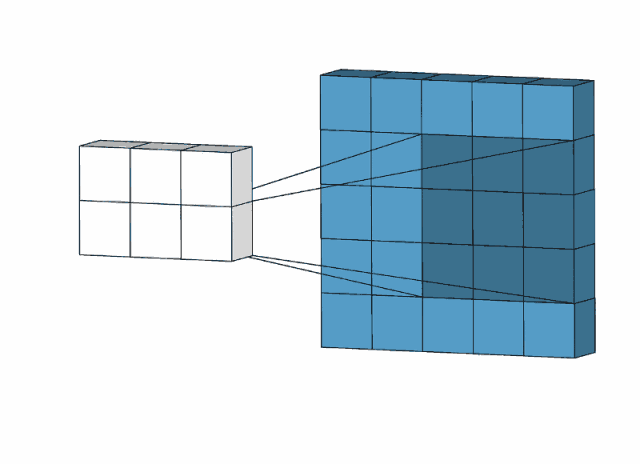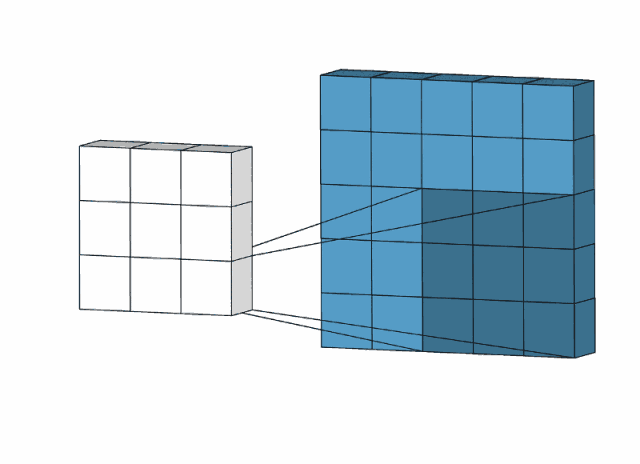
比如,我们用下面的卷积核
\[\text{kernel}=\begin{bmatrix} 1&0&-1\\ 0&0&0\\ -1&0&1\\ \end{bmatrix}\]对一个5*5图像
\[\text{img}=\begin{bmatrix} 1&3&1&0&4\\ 0&4&4&3&0\\ 1&2&4&0&4\\ 0&0&3&4&4\\ 4&0&0&2&2\\ \end{bmatrix}\]进行卷积操作,那么卷积核会按顺序遍历整个img,逐个进行哈达玛积(元素与元素相乘)再求和。比如这里,卷积核最开始和img左上角九个元素进行计算:
\[\begin{bmatrix} 1&0&-1\\ 0&0&0\\ -1&0&1\\ \end{bmatrix}⊙\begin{bmatrix} 1&3&1\\ 0&4&4\\ 1&2&4\\ \end{bmatrix}=\begin{bmatrix} 1&0&-1\\ 0&0&0\\ -1&0&4\\ \end{bmatrix}\]然后再求和,也就是3,作为我们卷积结果的第一行第一列元素:
\[\begin{bmatrix} 3&?&?\\ ?&?&?\\ ?&?&?\\ \end{bmatrix}\]然后卷积核向右移动一格,和矩阵
\[\begin{bmatrix} 3&1&0\\ 4&4&3\\ 2&4&0\\ \end{bmatrix}\]进行卷积求和,作为卷积结果的第一行第二列元素,以此类推,卷积结果是一个3*3的矩阵:
\[\begin{bmatrix} 3&1&-3\\ -1&5&5\\ -7&4&2\\ \end{bmatrix}\]对于一个三通道的图片,也就是有三个img矩阵,卷积核应该是逐通道分别卷积,卷积后生成的就是3*3*3的图片。
Stride
stride就是步的意思,在卷积的时候,我们不需要像上面那样一步一步地卷积,而是隔几步一次卷积。还是拿下面的矩阵举例:
\[\text{img}=\begin{bmatrix} 1&3&1&0&4\\ 0&4&4&3&0\\ 1&2&4&0&4\\ 0&0&3&4&4\\ 4&0&0&2&2\\ \end{bmatrix}\]当stride为2,使用3*3的卷积核,第一步还是和左上角的九个元素作卷积,但第二次跨了一步,是和
\[\text{img}=\begin{bmatrix} 1&0&4\\ 4&3&0\\ 4&0&4\\ \end{bmatrix}\]作卷积,这样的卷积生成的就是2*2矩阵。stride机制的加入可以使参数进一步减少,但更深层次的好处是减少了像素特征的重叠。
对于一个$N\times N$的图像输入,卷积核大小为$F\times F$,步长Stride为$S$,那么输出的尺寸:
\[O=1+\dfrac{N-F}{S}\]也就是$O\times O$的输出。
Padding
卷积操作的缺点之一是可能在图像边界上存在的信息的丢失。因为它们只有在卷积核滑动时才被捕获,所以它们永远没有机会被看到。解决这个问题的一个非常简单但有效的方法是使用零填充。零填充的另一个好处是管理输出大小。比如补零后的5*5数据变成了7*7,如下:
\[\begin{bmatrix} 0&0&0&0&0&0&0\\ 0&1&3&1&0&4&0\\ 0&0&4&4&3&0&0\\ 0&1&2&4&0&4&0\\ 0&0&0&3&4&4&0\\ 0&4&0&0&2&2&0\\ 0&0&0&0&0&0&0\\ \end{bmatrix}\]这样,如果令stride为1,也就是每次只移动一格,3*3的卷积核对数据进行卷积后,图片仍是5*5的。也正因如此,上面的公式需要修正:
\[O=1+\dfrac{N+2P-F}{S}\]$P$就是0填充的环数,比如这里就是1. Padding帮助我们防止网络输出大小随着深度的增加而缩小。因此,任意层数的深度卷积网络成为可能。
CNN的特征
权重共享(即始终使用同一个卷积核)给模型带来了不变性的转换。它有助于过滤学习特性,而不管空间特性(比如位置与旋转角度)如何。通过随机化卷积核,它们将学习上面那样的检测边缘,如果这样能提高学习表现。重要的是,如果对于输入来说空间特性是一个重要特征,那么使用共享权重是一个非常糟糕的主意。
这个概念也可以扩展到不同的维度。例如,如果是诸如音频的顺序数据,那么它可以使用一维音频。如果它是一个图像,则可以应用二维卷积。对于视频或三维图像,可以使用三维卷积。这个简单的想法击败了2012年ImageNet比赛中CV的所有经典的物体识别方法。
卷积公式
下面的公式是对上面卷积操作的形式化总结:
\[net(t,f)=(x*w)[t,f]=\sum_{m}\sum_{n}x[m,n]w[t-m,f-n]\]其中$net(t,f)$就是卷积后的输出,$x$是输入的图片,$w$是卷积核矩阵,”*“是卷积操作。
非线性层(Nonlinearity)
卷积后的下一层是非线性层。非线性层可用于调整或切断生成的输出。应用此层是为了使输出饱和或限制生成的输出。
多年来,Sigmoid和tanh是最流行的非线性函数。然而最近,修正线性单元(ReLU)更经常被使用,原因如下:
- ReLU在函数和梯度上都有更简单的形式。
- sigmoid和tanh在反向传播时易产生梯度消失,尤其是神经网络层数增加时。然而,ReLU对正输入有一个恒定的梯度。虽然该函数不可微分,但在实现中可以忽略它;
- ReLU创建了一个更稀疏的表示形式。因为梯度中的0导致得到值是完全的0。然而,Sigmoid和tanh的梯度结果总是非零的,这可能不有利于训练.
更多关于激活函数的细节可参考激活函数 Welt Xing’s Blog (welts.xyz),从理论和实现上探究和验证了激活函数间的区别。
池化层(Pooling)
池化的主要思想是降采样,以降低后面网络层的复杂性,可以认为类似于减少分辨率。
最大池化(Max-pooling)是最常见的池化方法之一。它将图像划分为子区域矩形,并且只返回该子区域内部的最大值。最大池化中最常用的大小之一是2×2:
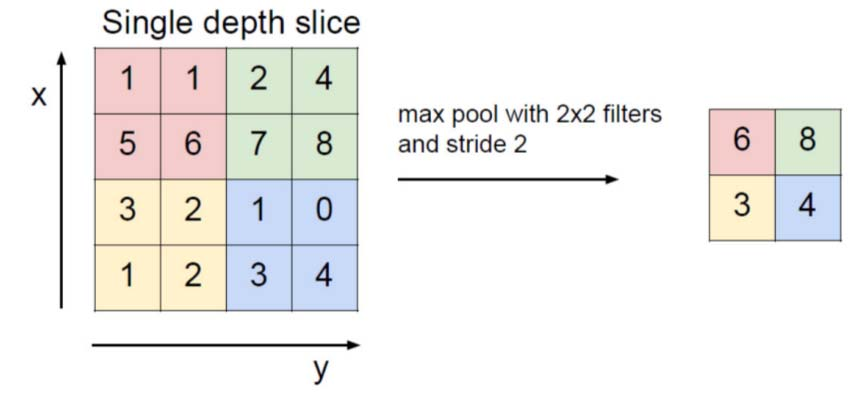
这意味着池化时的stride为2。为了避免降采样,可以令stride=1,但这并不常见。应该考虑到降采样并不能保留信息的位置。因此,只有在信息存在( presence of information )很重要(而不是空间信息)时才应该应用。此外,池化可以用于不相同的卷积核和stride,以提高效率。
全连接层
在池化结束后,将每一条数据转化成向量格式,送入全连接神经网络进行学习。全连接层的主要缺点是,它包含了许多参数,在训练例子中需要复杂的计算。因此,我们试图消除节点和连接的数量。使用dropout可以满足已删除的节点和连接。例如,LeNet和AlexNet在保持计算复杂度不变的同时设计了一个深且宽的网络。
流行的CNN结构
LeNet由Yan LeCun引入以进行数字识别,它有5个卷积层和一个全连接的层(如MLP):
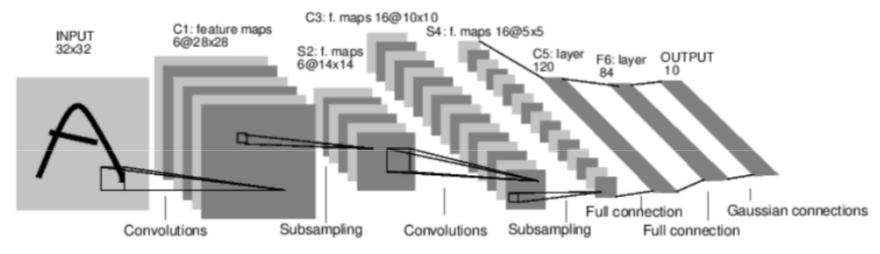
AlexNet有5个卷积层和2个全连接层。在第一、第二和第五卷积层之后进行最大池化。它总共有650K个神经元,60M个的参数和630M个连接。AlexNet是第一个证明深度学习在CV任务中是有效的模型。
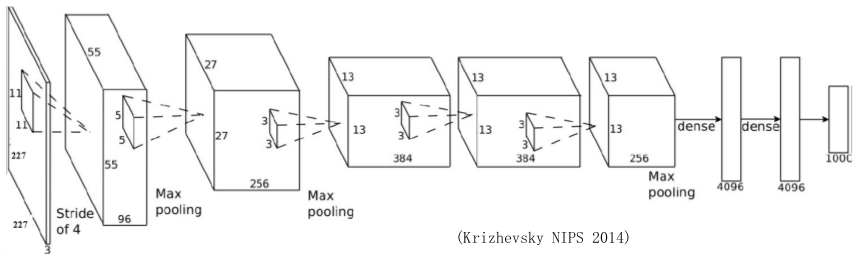
总结
我们讨论了与卷积神经网络(CNN)相关的重要问题,并解释了各参数对网络性能的影响。CNN中最重要的一层是卷积层,它需要网络内的大部分时间。网络性能还取决于网络层数。但另一方面,随着层数增加,训练和测试网络所需的时间也有所延长。今天,CNN认为是机器学习中的全功率工具,为许多应用程序,如人脸检测和图像,视频识别和语音识别。