An overview of gradient descent optimization algorithms

原文地址：https://arxiv.org/abs/1609.04747

摘要

虽然梯度下降优化算法越来越流行，但仍被视作黑箱（black-box）优化器，因为很难对它们的优点和缺点进行实际的解释。这篇文章旨在为读者提供关于不同算法的直观解释，从而更好使用它们。在此概述过程中，我们将研究梯度下降的不同变体，引入最常见的优化算法，在并行和分布式环境中回顾体系结构，并研究优化梯度下降的其他策略。

引言

梯度下降是最常用的优化算法之一，也是优化神经网络的最常见方法。与此同时，每个先进的深度学习库都包含了优化梯度下降的各种算法，以优化梯度下降，比如lasagne , caffe , 和keras。然而，这些算法经常被用作黑箱优化器，因为很难得到对其优缺点的实际解释。

梯度下降的思想和一些例子可以参考笔者的https://welts.xyz/2021/08/18/iteralgo/。因此在这里不作过多介绍。

我们对下面出现的基本符号做出约定：

• $\theta$：$\theta\in\mathbb{R}^d$，是我们需要优化的参数；
• $J$：目标函数，也就是损失函数；
• $\nabla_\theta J(\theta)$：函数$J$对参数$\theta$的梯度。

梯度下降变种（Gradient Descent Variants）

梯度下降有三种变体，差异体现在在使用多少数据来计算目标函数的梯度上。根据数据量，我们会在参数更新的准确性和耗时之间进行权衡。

批梯度下降

Batch gradient descent，也就是GBD，也被称作Vanilla gradient descent，也就是最原始的梯度下降。

Vanilla是神经网络领域的常见词汇，比如Vanilla Neural Networks、Vanilla CNN等。Vanilla本意是香草，在这里基本等同于raw。比如Vanilla Neural Networks实际上就是BP神经网络，而Vanilla CNN实际上就是最原始的CNN。

一次梯度更新需要所有的训练数据：

由于我们需要计算整个数据集的梯度才只执行一次更新，批梯度下降可能非常缓慢，并且对于内存无法容纳的数据集是很棘手的。

伪代码（仿Python）：

for i in range (nb_epochs):
	params_grad = evaluate_gradient(loss_function, data, params)
	params = params - learning_rate * params_grad

在一些深度学习库中已经实现了自动微分机制，因此可以很快求出梯度。然后沿着梯度的方向更新参数，学习速率$\eta$决定了我们执行更新的大小。批梯度下降会收敛到凸误差曲面的全局最小值，对非凸曲面收敛到局部最小值。

随机梯度下降

Stochastic Gradient Descent，也就是SGD，与BGD完全相反，是对每个训练样例$(x^{(i)},y^{(i)})$求梯度和更新：

批梯度下降对大型数据集执行冗余计算，因为它在每次参数更新之前重新计算类梯度。SGD通过每次执行一次更新来消除这种冗余。因此，它通常要快得多，也可以用来在线学习。SGD以高方差频繁更新，导致目标函数波动，如图所示：

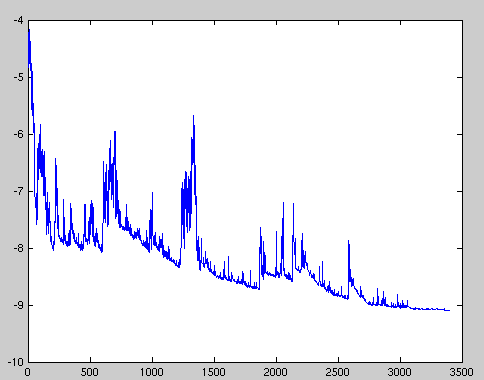
当批梯度下降收敛于盆地（basin）的最小值时，SGD的波动可以使其能够跳到新的、可能更好的局部最小值；另一方面，这最终使收敛到$J$最小值，SGD使得模型过拟合（文中用的是overshooting）。然而，研究表明，当我们缓慢降低学习率时，SGD表现出与BGD同的收敛行为，几乎可以肯确定对于非凸优化和凸优化问题分别收敛到局部或全局最小值。

伪代码（注意到打乱数据）：

for i in range (nb_epochs):
	np.random.shuffle(data)
	for example in data:
		params_grad = evaluate_gradient(loss_function, example, params )
		params = params - learning_rate * params_grad

小批次梯度下降

Mini-batch Gradient Descent将上述两种梯度下降进行了trade-off，每次更新只使用$n$个训练样本：

这样做的优点：

• 可以减少参数更新的方差，从而收敛更加稳定；
• 可以利用最先进的深度学习库中实现得很好的矩阵优化，从而非常高效地计算一个小批量数据的梯度。

常见的mini-batch大小范围在50到256之间，但由于不同的应用场景可能有所不同。小批量梯度下降通常是训练神经网络时的首选算法，即使在使用mini-batch GD时通常也称作SGD。为了简单起见，本文其余部分省略了参数$x^{(i：i+n)}；y^{(i：i+n)}$。

下面是mini-batch大小设为50时的伪代码：

for i in range (nb_epochs):
	np.random.shuffle(data)
	for batch in get_batches(data, batch_size =50):
		params_grad = evaluate_gradient(loss_function, batch, params )
		params = params - learning_rate * params_grad

挑战（Challenges）

小批梯度下降虽然有优点，但也带来了一些挑战：

• 选择一个合适的学习率可能是困难的（调参）。学习率过小则收敛太慢，而过学习率太大会阻碍收敛，并导致损失函数在最小值附近波动，甚至发散；

• 现如今有一些随着训练过程调整学习率的方法，比如根据预定义的时间降低学习率，或当目标变化低于阈值时去降低。然而，这些时间和阈值必须提前定义，而事实上它们会随着数据集的特征而变化；

• 此外，所有参数的更新共享了相同的学习率。如果我们的数据稀疏，并且我们的特性有非常不同的频率（”have very different frequencies”），我们也许不希望更新全部，而是对很少发生的特性执行更大的更新（” a larger update for rarely occurring features”）。

• 对于最小化神经网络中常见的高度非凸误差函数，我们需要避免函数点被困在它们的众多次优局部极小值中。有些学者则认为困难实际上不是来自局部最小值，而是来自鞍点。一个维度向上倾斜，另一个维度向下倾斜的点。这些鞍点通常被一个具有相同误差的平台所包围，这使得SGD逃逸是出了名的困难，因为梯度在所有维度上都接近于零：

  

梯度下降优化算法

文章在这里会介绍广泛使用的用于应对上述挑战的算法。二阶方法，如牛顿法不会被讨论，因为它们“在高维数据集的实践中不可行”。

动量机制

SGD会在所谓的峡谷（ravine）处沿着下降路径出现振荡：

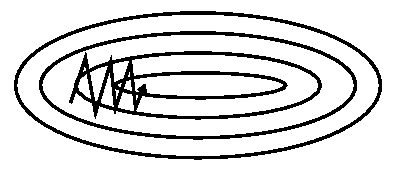
动量机制（Momentum）通过保存上一轮更新的信息推动本轮更新：

通过将上次的更新向量添加到当前更新向量，动量机制可以加速下降并减小振荡：

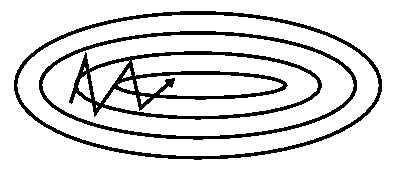
动量项系数$\gamma$通常设为0.9或附近的值。如果把梯度下降比作是一个小球从山顶掉下山坡，BGD可以理解为几乎匀速，平和地下降；加入了动量机制后，我们需要考虑之前的运动，小球的速度只会比上一次更快：对于梯度指向相同方向的维度，动量项增加了，并减少了对梯度变化方向的维度的更新。

Nesterov加速梯度

然而，一个盲目地沿着山坡滚下来的球是无法令我们满意的。我们想要有一个更聪明的球，一个知道它要去哪里的球，这样它就能在山坡由下降变为上升（也就是到达局部极小点）之前放慢速度

Nesterov Accelerated Gradient(NAG)便基于上述想法。我们使用动量项$γv_{t−1}$来移动参数$\theta$。NAG计算$θ−γv_{t−1}$，也就是下一个位置的近似（并不是精确更新，只是近似）。我们计算的不是更新前的梯度，而是更新后大致位置的梯度：

文章借用了Hinton教授的一门课程的slide配图来可视化上述过程：

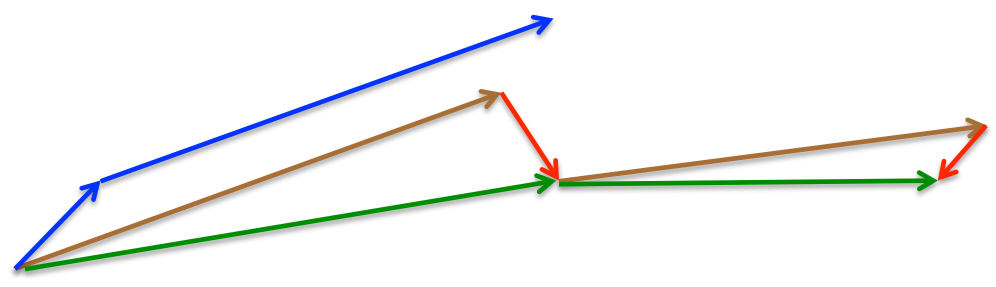
蓝色小箭头是矢量$-\nabla_\theta J(\theta)$，朴素的梯度下降使得$\theta$沿着该矢量移动；蓝色长箭头对应$-\gamma v_{t-1}$，$\theta$再沿着它去移动，便是动量机制下梯度下降的结果；棕色的长箭头和蓝色长箭头所对应的矢量相等，然后红色小箭头对应的是矢量$-\eta\nabla_\theta J(\theta−\gamma v_{t−1})$，也就是NAG中下一步大致位置的梯度，它被视作是梯度的一个矫正（Correction），绿色箭头是NAG算法单次下降$\theta$的运动轨迹。

现在，我们能够使更新适应损失函数的斜率，并反过来加速SGD，我们同时也希望更新适应每个单独的参数，以根据它们的重要性执行更大或更小的更新。

Adagrad

Adagrad是一种基于梯度的优化算法：它让学习率适应参数，对不频繁参数（infrequent parameters）执行更大的更新，对频繁参数（frequent parameters）执行更小的更新。因此，它非常适合处理稀疏数据。迪恩等人发现，Adagrad大大提高了SGD的鲁棒性，并将其用于在谷歌训练大规模神经网络，它还学会了在Youtube视频中识别猫。此外，彭宁顿等人使用Adagrad训练GloVe词嵌入，因为不频繁单词比频繁单词需要更大的更新。

之前，我们一次性对所有参数θ进行了更新，因为每个参数$\theta_i$使用相同的学习率$\eta$。由于Adagrad在每次对每个参数$\theta_i$使用不同的学习率，我们首先展示Adagrad的每个参数更新，然后我们对其进行向量化。为了简洁起见，我们设置$g_{t,i}$为目标函数对参数$\theta_i$在$t$时刻的梯度：

因此SGD的更新可以改写成：

Adagrad则是为每一个参数$\theta_i$选择其独特的学习率进行梯度下降：

其中$G_t\in\mathbb R^{d\times d}$是一个对角矩阵，$G_{t,ii}$对应$t$次更新下损失函数对$\theta_i$的梯度平方和。$\epsilon$是为防止分母为0而设置的一个平滑项，通常设$1e-8$。文章说如果分母没有进行开平方操作，则效果会变差。

我们可以将Adagrad更新向量化：

其中$\odot$是矩阵-向量的元素对应乘积（笔者认为矩阵乘法也是可以的），这样就可以直接更新所有参数。

Adagrad的一个好处是不需要手动调整学习率，大多数直接默认设置为常数0.01。

该算法的一个不足就是随着训练轮次的积累，也就是$t$的增加，由于$G_t$计算的是平方和，所以其元素不断增大，从而使学习率下降并趋于0，这样$\theta$便不再移动。下面的Adadelta算法就是为解决这一问题而设计。

Adadelta

Adadelta是Adagrad的延伸，致力于解决Adagrad中过快衰减到0的学习率的问题。Adadelta没有积累所有过去的平方梯度，而是将计算梯度范围的窗口限制在某个固定大小的$w$。

存储$w$个之前的平方梯度是低效的（比如用FIFO队列实现），因此梯度平方和被递归地定义为所有过去平方梯度的衰减平均值：

这里的参数$\gamma$和动量机制中的参数含义类似，应设置在0.9附近。类似Adagrad，我们写出Adadelta更新的向量形式：

由于分母对应的是梯度的均方根误差（不是均方误差），因此将其简写成：

从下面开始就没怎么看懂：文章说这样的更新从单位上说是不匹配的，参数$\theta$也应该有一个类似的项：

参数更新的均方根误差：

用均方根误差去替代学习率$\eta$：

可以发信Adadelta不需要事先设置学习率，因为它在更新规则中被消掉了。

RMSprop

RMSprop是Geoff Hinton提出，但并未发表的学习率调解法。其形式和Adadelta开始的形式相同：

Hinton建议将$\gamma$设置为0.9，$\eta$设置为0.001较好。

Adam

Adaptive Moment Estimation（Adam）是另一种计算每个参数的自适应学习率的方法。除了像Adadelta和RMSprop存储过去平方梯度$v_t$的指数衰减平均外，Adam还保持了过去梯度mt的指数衰减平均值，类似于动量机制：

$m_t$和$v_t$分别是一阶矩（均值）和二阶矩（非中心方差）的估计量，这也是Adam名字的由来（自适应矩估计）。当它们被初始化为零向量，Adam的作者观察到它们偏向于零，特别是在初始几步，特别是当衰减速率很小时(即$β_1$和$β_2$接近1)。

因此通过下式来矫正偏差：

以此进行Adam更新：

作者建议如下的参数设置：$\beta_1=0.9,\beta_2=0.999,\epsilon=1e-8$。

AdaMax

AdaMax是将上面的Adam的一些公式进行扩展：

AdaMax将$p$范数设置为无穷范数：$l^\infty$。无穷范数满足：

因此$v_t$的更新变成了：（用$u_t$去代替，防止和Adam中的更新混淆）

AdaMax的更新规则：

因为有个$\max$最大化操作，因此就不会偏向于0，从而不需要像Adam那样去矫正。

建议的参数设置：$\eta=0.002,\beta_1=0.9,\beta2=0.999$。

由于过于复杂，这里省略后面的Nadam方法。

可视化

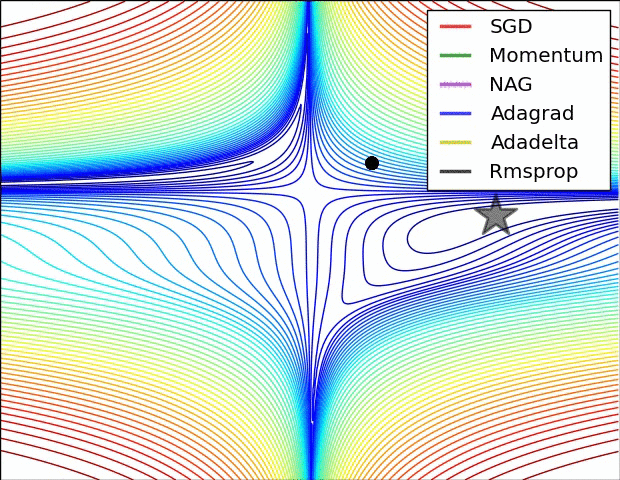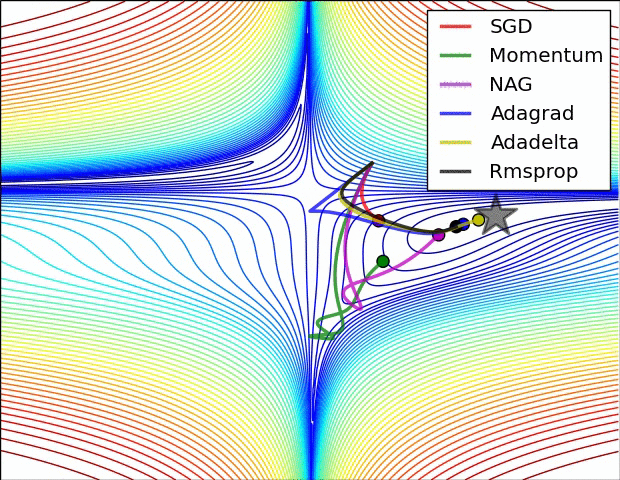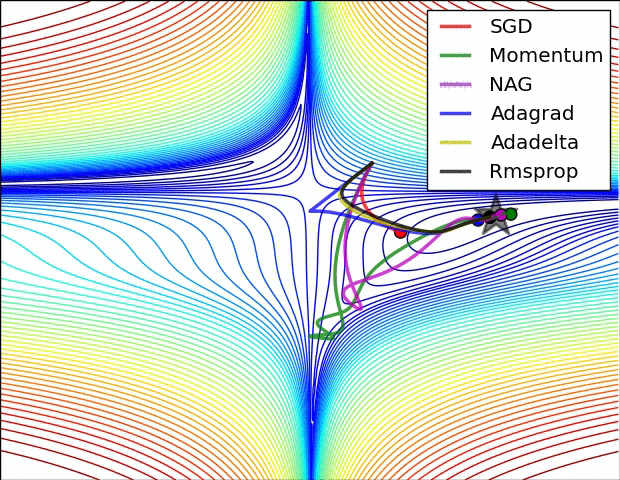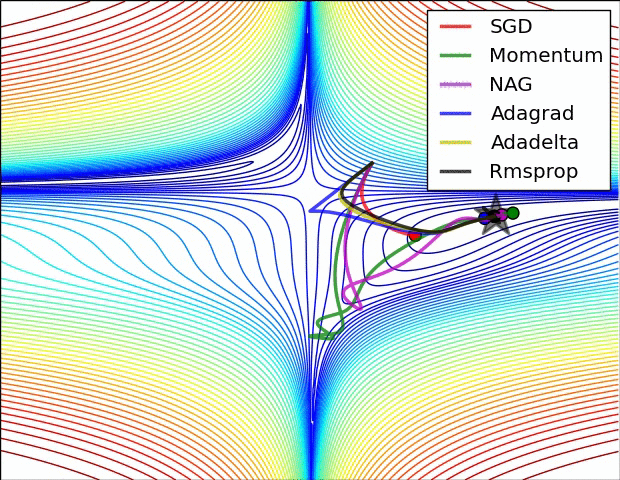
在上图中，我们看到了它们在损失函数（the Beale function）轮廓上的路径。所有这些下降都在同一点开始，并采取不同的路径来达到最小值。请注意，Adagrad、Adadelta和RMSprop立即向正确的方向移动，收敛速度相似，而动量和NAG被带出轨道，让人想起一个球滚下山上的场景。然而，NAG能够更快地纠正其路线，因为它通过展望未来，增加了反应能力，从而走向最优处。

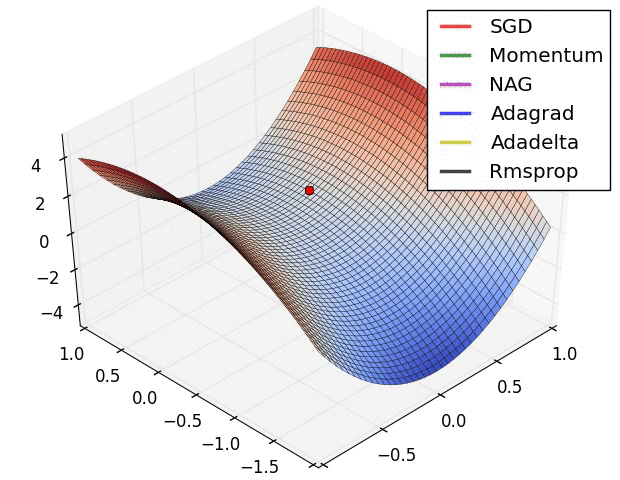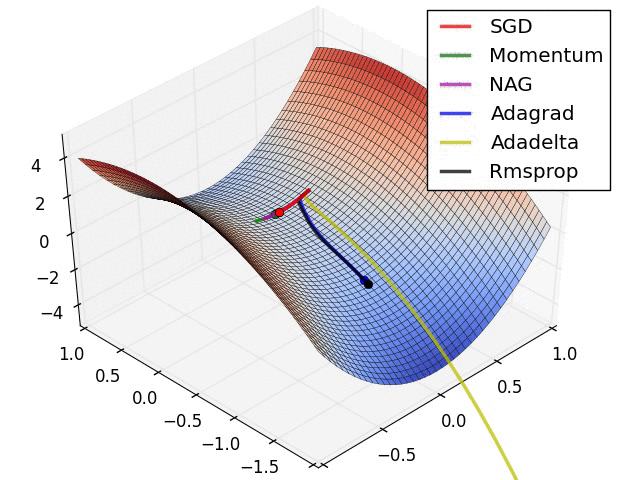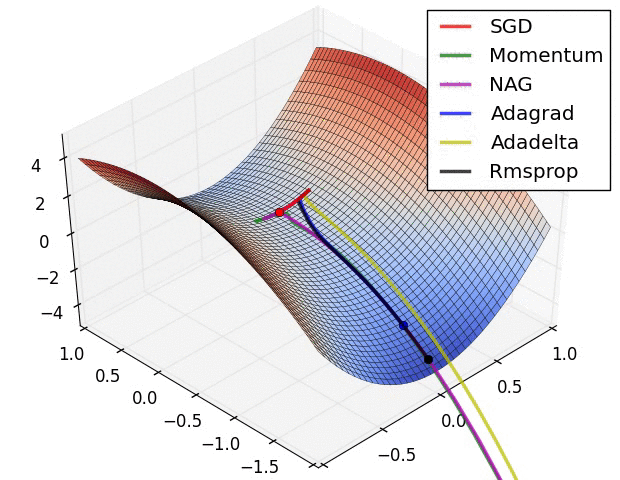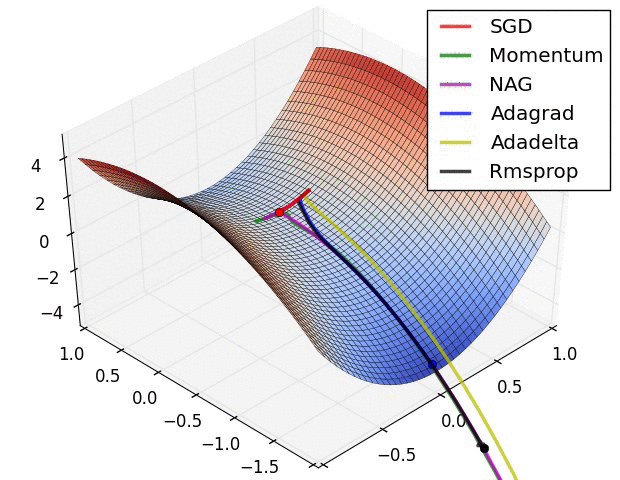
上图显示了算法在鞍点上的行为。一个维度有正斜率，而另一个维度有负斜率，这就像我们前面提到的那样给SGD带来了困难。请注意，SGD、动量和NAG发现很难打破对称，尽管后者两个最终设法逃脱了鞍点，而Adagrad、RMSprop和Adadelta快速冲向负斜坡，其中Adadelta下降得最快。

可以发现梯度下降优化算法的应用使得梯度下降有更好的收敛性。

如何选择？

如果输入数据稀疏，那么可能使用自适应学习速率方法获得最佳结果。另一个好处是，我们不再需要调整学习速率，使用默认值就可以获得最佳结果。总体上说，Adam是最好的选择。

有趣的是，许多最近的论文使用没有动量的SGD和一个简单的学习率退火时间表。SGD通常可以找到一个最小值，但它可能需要比一些优化器长得多的时间，更依赖于一个稳健的初始化和退火计划，并可能被困在鞍点而不是局部最小值。因此，如果关心快速收敛，训练一个深度或复杂的神经网络，您应该选择一种自适应学习速率方法。

并行化和分布式SGD

考虑到大规模数据解决方案的普遍性和低商品集群的可用性，分发SGD以进一步加速它是一个明显的选择。SGD本质上是顺序计算的：step by step，向最小值前进。它可以提供良好的收敛性，但可能速度很慢，特别是在大型数据集。相比之下，异步运行SGD的速度更快，但计算设备之间的通信会导致收敛性较差。此外，我们还可以在一台计算机上并行化SGD，而不需要大型计算集群。由于不是文章重点，只一笔带过。

优化SGD的其他策略

以下是一些其他的策略，可以与上述任何算法一起使用，以进一步提高SGD的性能。

• 数据打乱和Curriculum learning：由于不想让训练出的模型学习到数据的顺序特性，每次将数据打乱是一个好主意；然而在有些情况下（如训练LSTMs），控制顺序会带来更好的收敛性，这就是Curriculum learning的范畴了；
• Batch normalization：批标准化，在神经网络训练中，对每个隐藏层的输入都做一次标准化，防止正向传播时的函数值越来越边缘化；
• Early stopping：早停，在梯度下降的同时计算测试集误差，防止过拟合；

• Gradient noise：梯度噪声，对计算的梯度加上正态分布的噪声：

  \[g_{t,i}=g_{t,i}+N(0,\dfrac{\eta}{(1+t)^\gamma})\]

  研究表明，添加这种噪声可以使网络对于较差的初始化更健壮，并有助于训练深度和复杂的网络。一种可能是增加的噪声给了模型更多的机会逃逸和找到新的局部最小值，而这些最小值对于更深层次的模型更常见。

结语

本文最初研究了三种梯度下降的变量，其中小批梯度下降是最流行的。然后，文章介绍了最常用于优化SGD的算法：动量、内斯特罗夫加速梯度、Adagrad、Adadelt、RMSprop、Adam、AdaMax、Nadam，以及优化异步SGD的不同算法。最后，我们考虑了其他改进SGD的策略，如打乱数据和Curriculum learning、批标准化和早停。

• Previous
  泛函分析论
• Next
  实变函数论