常用的迭代优化算法

引言

在学习机器学习的过程中，我们总是避不开优化问题，而且这些问题常常没有解析解。而在计算机算力不断增强的今天，迭代算法由于其计算的重复性和可并行性渐渐受到欢迎。这里我们会简单描述几种常见的迭代优化算法。

梯度下降法

引入

我们先从$\mathbb{R}$上的函数说起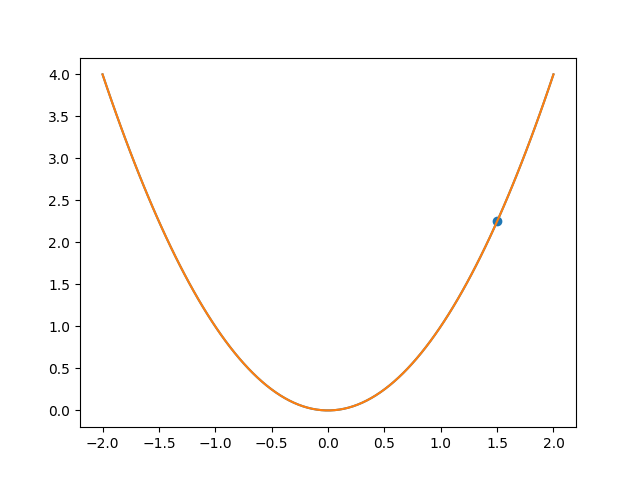， 假设我们正处于$(1.5,2.25)$处，如果我们想要到达最小值点，那么必然是向下走，这里的“下”其实就是导数为负的意思，这就是梯度下降法的朴素思想：如果一个函数是凸函数，那么我们可以不断“向下跑”得到。

由于计算机无法处理连续态下的问题，所以下降只能通过离散化的不断迭代实现：我们制定一个步长$\eta$，不断循环

直到$f(x^{(k+1)})=f(x^{(k)})$，或者宽容一点，$\vert f(x^{(k+1)})-f(x^{(k)})\vert\lt\epsilon$.

对上面这个例子去进行“导数”下降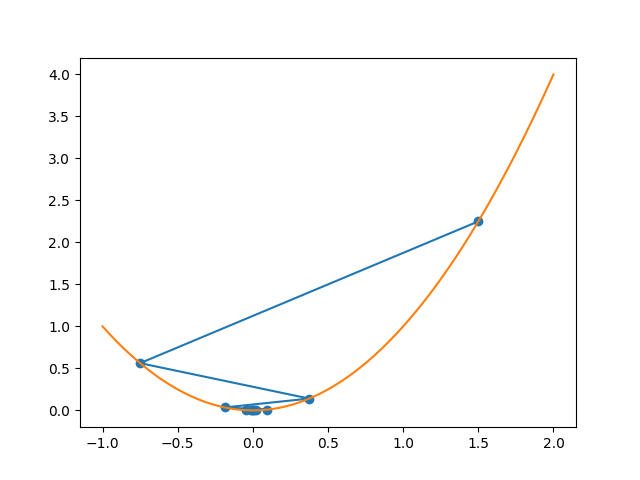： 我们选取了较大的步长$(0.75)$，因此会产生振荡，但最后到达了极值点附近。

真正的梯度下降

我们刚才只能算是“导数下降”，但梯度下降也就是将$\mathbb{R}$上函数扩展到$\mathbb{R}^n$，正如梯度就是导数在多维欧几里得空间的推广：

可以证明，梯度向量的方向是函数下降速度最快的方向。我们尝试对二元函数$f(x_1,x_2)=x_1^2+x_2^4$进行梯度下降求解，容易知道其梯度

import matplotlib.pyplot as plt
import numpy as np

# 初始点设置为(4, 3)
x1 = [4]
x2 = [3]

eta, epsilon = 0.01, 1e-10

f = lambda x1, x2 : x1**2 + x2**4

while True:
    x1k, x2k = x1[-1], x2[-1]
    der1, der2 = 2 * x1k, 4 * x2k**3
    x1k_new = x1k - eta * der1
    x2k_new = x2k - eta * der2
    x1.append(x1k_new)
    x2.append(x2k_new)
    if abs(f(x1k_new, x2k_new) - f(x1k, x2k)) < epsilon:
        break

效果如下

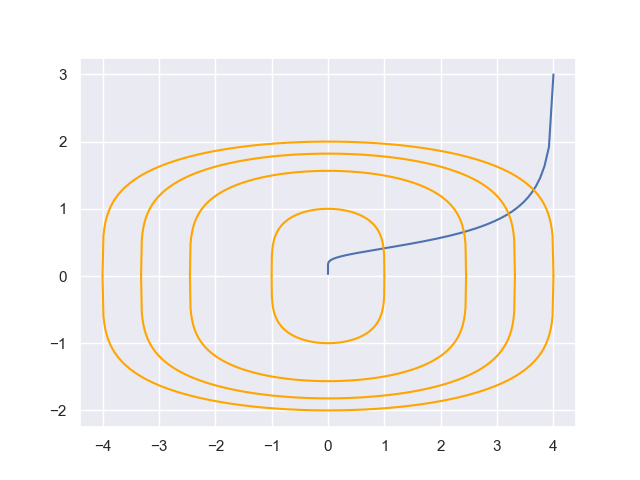
其中黄色部分为函数等高线$x_1^2+x_2^4=k$.

缺陷

我们前面提到过，当目标函数是凸函数时，梯度下降法得到的确实是全局最优解；而一般情况下不保证是全局最优的，比如下图：

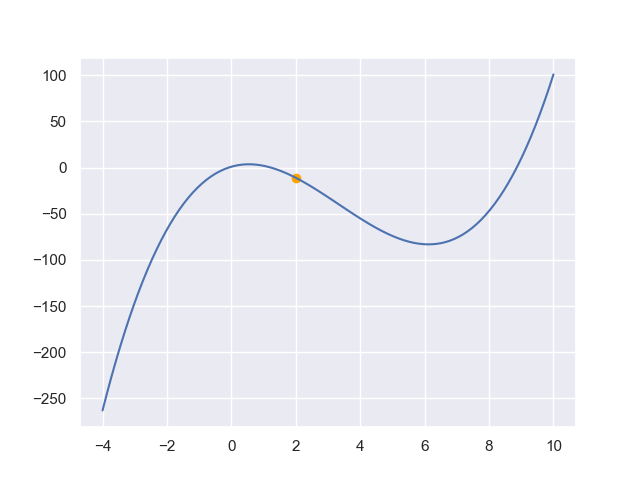
此外，梯度下降的收敛速度也不是很快.

牛顿法

和梯度下降类似，牛顿法也是求解无约束优化问题常用的迭代算法，拥有下降速度快的特点。事实上牛顿法原本是用来近似求解方程的方法，因此我们从它最根本的目的开始

从低维情况开始

这里我们从简单的$\mathbb{R}$上二次函数$y=2x^2+3x-5$说起：

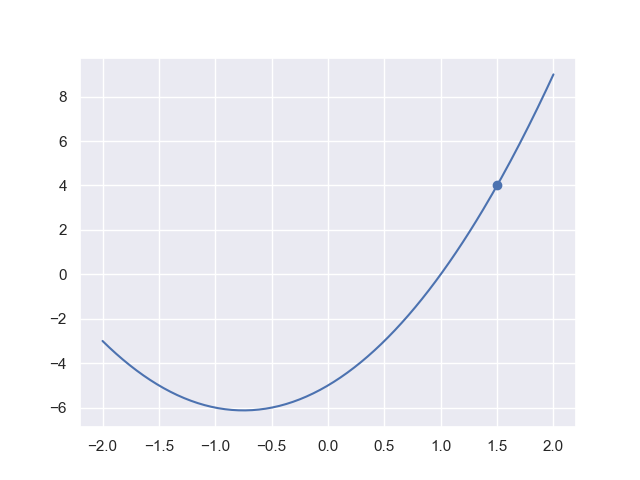
我们现在处于$(x_0,y_0)=(1.5,4)$的位置，我们想找到$y=0$的解。类似于梯度下降，我们也可以不断向解所在的方向行走直到到达解的位置。显然，行走方向由点所处的位置决定：

或许大家会想到类似这样的迭代公式：

恰好能符合上面的移动规则，而这就是牛顿法：它首先作一条过$(x_0,f(x_0))$的切线：

得到其零点：

这种方法符合上面的移动规则，从而达到逼近方程零点的目的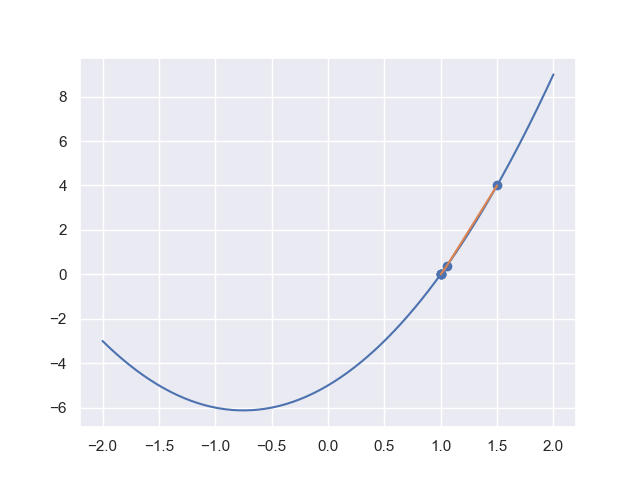： 可以发现它很快逼近了零点$x=1$. 那么牛顿法是如何将求零点和最优化联系起来的呢？这里我们有高等数学的一个定理：可微函数的极值点必是驻点（驻点就是导函数零点）。这启发我们，通过牛顿法寻找导函数$f’(x)$的零点，进而得到极值点。

我们对$f(x)$进行$x_0$附近的泰勒展开：

当$f’(x)=0$，对上式求导，我们有

进而

与上面的求解方程的牛顿法形式相同。我们知道泰勒公式的等号只有在$x\to x_0$时才成立，当$x$与$x_0$误差较大时，$f’(x_0-\dfrac{f’(x_0)}{f’‘(x_0)})\neq0$，但我们知道$x_0-\dfrac{f’(x_0)}{f’‘(x_0)}$与$x_0$相比更加接近我们的目标，于是将该式迭代使用。

我们还是用四次函数$y=x^4-x^3+x^2-x+1$作为例子，但这次是去求解极值点：

x_list =[-2] # 初始点设-2

f = lambda x : x**4 - x**3 + x**2 - x + 1
df = lambda x : 4*x**3 - 3*x**2 + 2*x - 1
d2f = lambda x : 12*x**2 - 6*x + 2

epsilon = 1e-10

while True:
    xk = x_list[-1]
    xk_new = xk - df(xk) / d2f(xk)
    x_list.append(xk_new)
    if abs(df(xk_new)) < epsilon:
        break

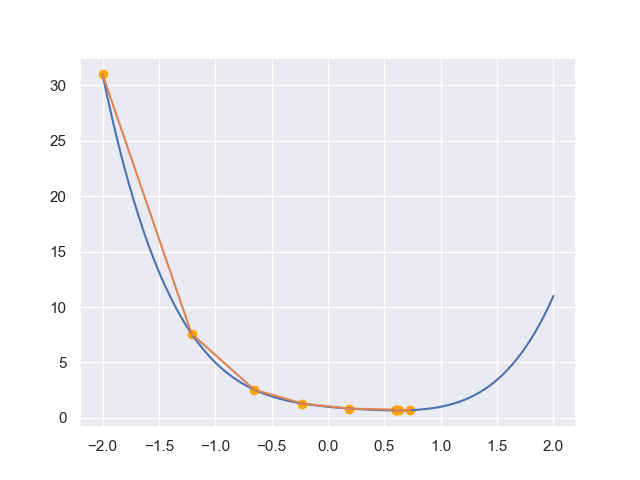可以发现通过牛顿法我们可以更快逼近极值点.

$\mathbb{R}^n$下的牛顿法

我们只需要写出$n$维情况下的展开，便可以得到牛顿法的广义形式：

其中$H(x_0)$是一个$n$阶矩阵，其中每个元素满足

称作黑塞矩阵。由偏导数性质，当函数连续，偏导数与求导顺序无关，因此$H$是对称矩阵。若$\nabla f(x)=0$，对上式求导则有

从而得出$n$元函数下的牛顿法迭代公式：

我们对函数$f(x_1,x_2)=\dfrac{1}{4}(x_1^4+2x_1^2x_2^2+x_2^4)$进行牛顿法测试求极值点：

# %%
import numpy as np

f = lambda x1, x2: (x1**4 + 2 * x1**2 * x2**2 + x2**4) / 4
df = lambda x1, x2: np.array([
    [x1**3 + x1 * x2**2],
    [x2 * x1**2 + x2**3],
])
d2f = lambda x1, x2: np.array([
    [3 * x1**2 + x2**2, 2 * x1 * x2],
    [2 * x1 * x2, x1**2 + 3 * x2**2],
])

# 起始点(3, 4)
x1 = [3]
x2 = [4]

epsilon = 1e-10

while True:
    x1k, x2k = x1[-1], x2[-1]
    x_new = np.linalg.inv(d2f(x1k, x2k)) @ df(x1k, x2k)
    x1k_new, x2k_new = x_new.T[0]
    print(x1k_new, x2k_new)
    x1.append(x1k_new)
    x2.append(x2k_new)
    new_gradient = df(x1k_new, x2k_new)
    if np.sum(new_gradient) / 2 < epsilon:
        break

结果如下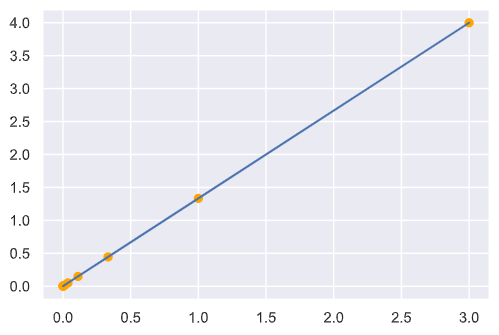： 迭代坐标：

3 4
0.9999999999999999 1.3333333333333333
0.33333333333333337 0.4444444444444443
0.11111111111111109 0.1481481481481481
0.03703703703703703 0.049382716049382706
0.012345679012345673 0.016460905349794237
0.004115226337448557 0.0054869684499314125
0.0013717421124828525 0.0018289894833104707
0.0004572473708276174 0.0006096631611034901
0.00015241579027587248 0.00020322105370116335

迭代速度很快，但注意到我们每次都需要求解一次矩阵的逆，计算较为复杂，由此引入下面的拟牛顿法。

拟牛顿法

我们希望能找到一个黑塞矩阵的逆的替代矩阵，这就是拟牛顿法的基本思想。先来看看牛顿法迭代中黑塞矩阵满足的条件，当我们位于$x_0$时，下一步迭代要到达的$x$满足泰勒展开式

对$x$求导，整理：

记$y_k=\nabla f(x^)-\nabla f(x^{(k)}),\delta_k=x^{(k+1)}-x^{(k)}$，则

上式便称作拟牛顿条件. 如果$H_k$正定，那么我们可以保证牛顿法搜索方向（也就是$x^{(k)}$的变化方向，$H^{-1}\nabla f$）是下降的，由此我们可以在保证方向正确的条件下步数更小地迭代：

将上面迭代关系式代入二阶泰勒展开式（用$g_k$代表$\nabla f(x^{(k)})$）：

由于$H_k$是正定矩阵，$H_k^{-1}$自然也时，因此二次型$g_k^\top H_k^{-1}g_k\geqslant0$，从而当$\lambda$为一个充分小的正数时，$f(x_1)<f(x_0)$，也就是说迭代方向确实是向着“下坡”的方向.

在拟牛顿法中将$G_k$作为$H_k^{-1}$的近似，则要求$Gk$：①每次迭代$G_k$正定；②满足拟牛顿条件：

根据拟牛顿条件选择$G_k$作为$H_k^{-1}$的近似或选择$B_k$作为$H_k$的近似的算法乘坐拟牛顿法。

根据拟牛顿条件，在每次迭代中需要更新矩阵$G_{k+1}$：

更新方法的不同导致了拟牛顿法的多种实现。

具体的实现算法

下面介绍的都是Broyden类拟牛顿法.

DFP算法

假设上面的矩阵迭代由$G_k$加上两个附加项构成：

为满足拟牛顿条件，我们需要找到合适的$P_k,Q_k$使得

因此我们可以使$P_k,Q_k$满足：

一个可满足的$P_k,Q_k$：

这样就有能得到迭代公式：

正式的算法如下：

$\textbf{function }\text{DFP}(f, \varepsilon,x,G)\textbf{ returns }x^\star:$
$\quad g\gets\nabla f(x)$
$\quad\textbf{if }|g<\varepsilon|$
$\qquad x^\star\gets x$
$\qquad\textbf{return }x^\star$
$\quad\textbf{while }\text{True}$
$\qquad p\gets -Gg$
$\qquad \lambda\gets\mathop{\arg\min}\limits_{\lambda\geqslant 0}f(x+\lambda p)$
$\qquad x\gets x+\lambda p$
$\qquad g\gets\nabla f(x)$
$\qquad\textbf{if }|g|\leqslant\varepsilon$
$\qquad\quad\textbf{break}$
$\qquad G\gets G+P+Q$
$\textbf{return }x$

BFGS算法

BFGS是目前最流行的拟牛顿法，它采取了和上面不一样的思路：通过近似$H_k$得到$B_k$并迭代。它也要满足拟牛顿条件：

而$B_k$和$B_{k+1}$的迭代使用的是和上面类似的方法：

找打合适的$P_k,Q_k$，得到矩阵的迭代公式：

BFGS算法过程和上面类似，唯一的不同就是上面是根据$p=-Gg$求出，这里是通过方程$Bp=-g$求出.

Broyden类算法

我们可以用BFGS中$B_k$的迭代得到相应$G_k$的迭代公式（计算过程较难，省略）：

成为BFGS算法关于$G_k$的迭代公式. 考虑到两种算法得到的$G$都符合拟牛顿条件，我们将两种算法导出的$G_{k+1}$记为$G^{\text{DFP}}$和$G^{\text{BFGS}}$，它们的线性组合

也满足拟牛顿条件，而且是正定的，这样我们就得到了一系列拟牛顿法，称为$\text{Broyden}$类算法.

• Previous
  ProtoNN:Compressed and Accurate kNN for Resource-scarce Devices
• Next
  南京大学2021春季：智能系统设计与应用