引言
按照《机器学习》西瓜书上的内容,我们实现了以Sigmoid为激活函数的单隐层神经网络。同时我们在之前的文章中说明了在代码框架中实现激活函数的替换是可行的。这里对激活函数进行一个总结并用我们设计的神经网络进行实验。
激活函数简介
在神经元模型中,神经元接收到来自其他神经元传递的输入信号,这些信号通过带权重的连接进行传递,“连接权重”相当于输入信号与神经元之间的“媒介”,当神经元接收到总数入值与阈值进行比较,然后通过“激活函数”处理来产生神经元的输出。
激活函数,理想中的激活函数是阶跃函数,输入值映射到输出值为“0”或“1”,“1”是神经元兴奋,“0”为神经元抑制。但是阶跃函数有不连续,不光滑等性质。因此我们想用一些连续的函数来近似阶跃函数,比如Sigmoid函数:
\[f(x)=\dfrac{1}{1+\exp(-x)}\]两者关系图像如下:
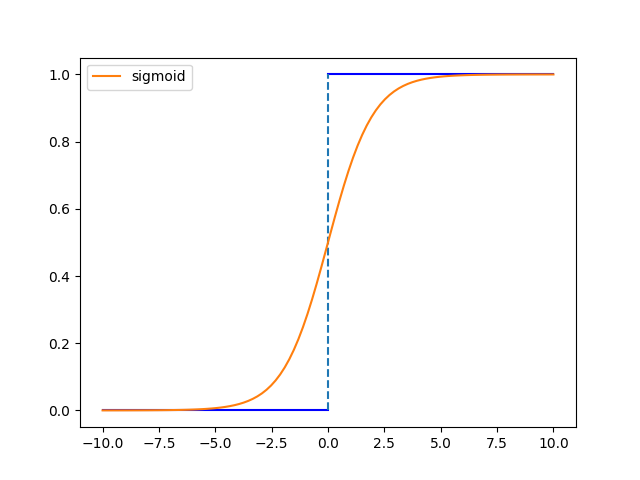
Sigmoid函数值域有限,单调连续并且求导容易,缺陷是幂运算提高了计算成本,其导数特性将带来梯度消失:我们知道Sigmoid函数满足
\[f'(x)=f(x)\big(1-f(x)\big)\]而$f(x)\in(0,1)$,两个$(0,1)$区间的数相乘会使数值更小。当深度增加时,反向传播中逐层求梯度会使梯度最终变成0,从而网络前端的权重参数无法更新,这就是梯度消失。
有些资料还提出Sigmoid的一个缺点:不是以0为中心,导致收敛速度下降。以现有知识,笔者无法解释。
类似的,$\tanh$函数和Sigmoid函数有相似的优缺点,但是以0为中心,收敛速度下降的问题有所改善:
\[f(x)=\dfrac{e^{x}-e^{-x}}{e^x+e^{-x}}\]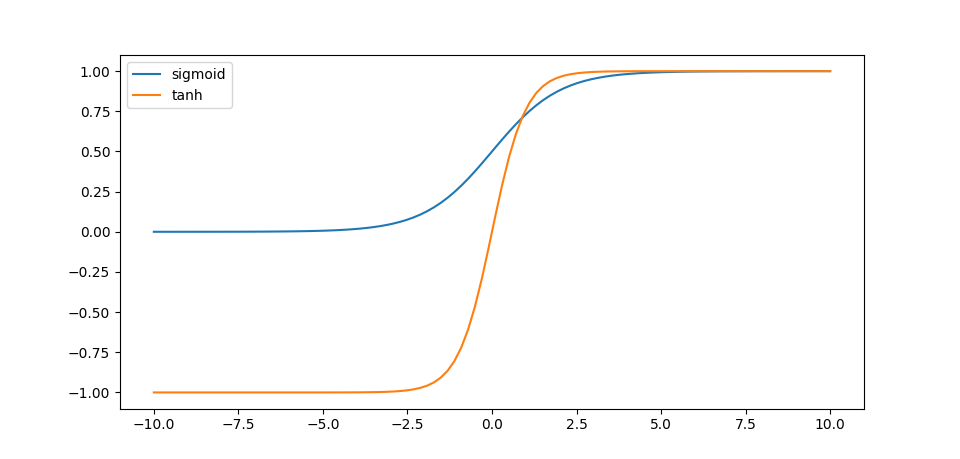
$\tanh$函数满足 \(f'(x)=1-f(x)^2\) 显然$\tanh(x)\in(-1,1)$,$f’(x)$仍处于$(0,1)$区间内,且随着反向传播趋近于0,有梯度消失的危险。
显然如果要避免梯度消失,我们就不能让激活函数限制在某一区间内。而Sigmoid和$\tanh$函数都有计算成本高的特点(计算指数),本着简单的原则,ReLU(Rectified Linear Unit)函数被提出:
\[f(x)=\max(x,0)\]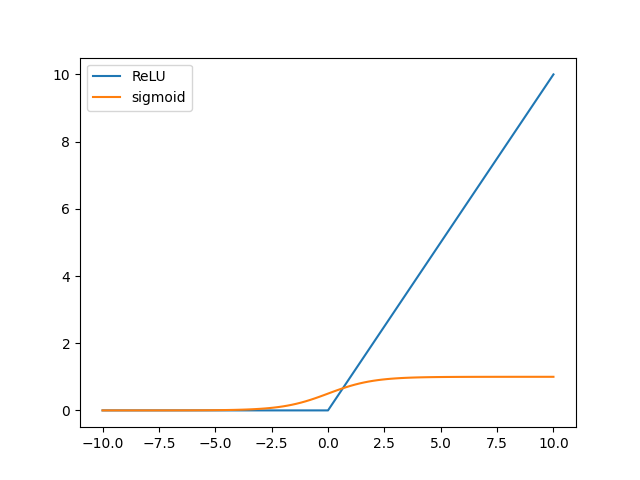
显然ReLU的梯度非0即1,。ReLU函数提高了收敛速度,且改善了梯度消失问题,且运算速度很快;而该函数会使得一些神经元的输出为0,从结构上缓解了过拟合。其缺点就是对参数初始化和学习率很敏感,考虑极端情形:所有的参数都是0,那么所有的神经元都会死亡;此外由于ReLU的输出和Sigmoid一样都是恒大于0,不以0为中心,影响网络收敛性。
对于上面的一些缺陷,带泄露的线性整流函数(Leaky ReLU)不会让神经元轻易死亡:
\[f(x)=\begin{cases} x,\;\;x\ge0\\ \alpha x,x<0 \end{cases}\]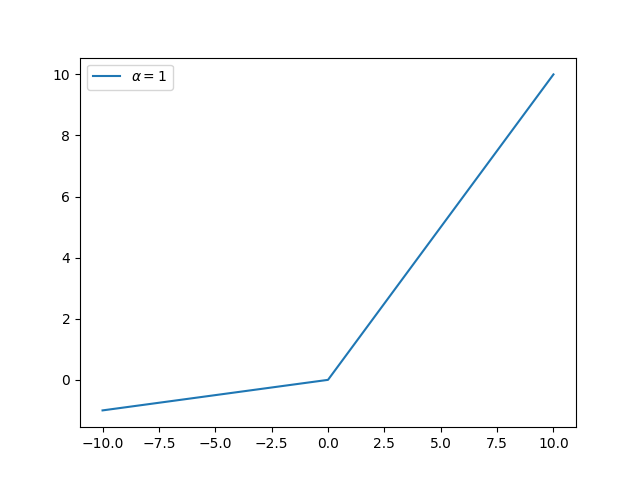
其中$0\lt \alpha\lt1$,而如果$\alpha$是学习的参数,或者是服从某一分布的随机数,那就是另外的算法了。
用多种激活函数进行学习
在我们自己设计的神经网络传播过程中:
(链接:ml-model-code/neuron.py at main · Kaslanarian/ml-model-code (github.com))
for epoch in range(epoches):
hidden = sigmoid(X @ self.__V - self.__G) # 隐藏层
output = sigmoid(hidden @ self.__W - self.__T) # 输出层
g = deriv_sigmoid(output) * (y - output) # 输出层
e = deriv_sigmoid(hidden) * (g @ self.__W.T) # 隐藏层
self.__W += lr * hidden.T @ g / X.shape[0] # 输出层
self.__T -= np.mean(lr * g, axis=0)
self.__V += lr * X.T @ e / X.shape[0] # 隐藏层
self.__G -= np.mean(lr * e, axis=0)
这里的两层激活函数都是sigmoid,理论上我们可以将这两层的激活函数进行替换,但为了遵循输出层Sigmoid的概率语义,我们最好只修改隐层的激活函数。
数据集,以及模型评估
这里我们将全Sigmoid激活函数网络作为对照组,为了保证结果比较的准确性,我们应确保网络的初始参数,训练集和测试集最好完全相同。
我们选择sklearn自带的breast_cancer(乳腺癌)数据集:
# 获取数据概况
from sklearn.datasets import load_breast_cancer
import numpy as np
X, y = load_breast_cancer(return_X_y=True)
print(X.shape, y.shape) # (569, 30), (569, 1)
print(np.unique(y)) # array([0, 1])
我们可以知道,该数据有30个特征,两个类别。我们预处理X, y并设计一个30*50*2的神经网络:
X = (X - X.mean()) / X.std() # 中心化和标准化对神经网络学习很重要
y = np.array([y]).T
one_hot_model = OneHotEncoder(sparse=False)
one_hot_model.fit(y)
train_X, test_X, train_y, test_y = train_test_split(X, y, train_size=0.7)
train_y = one_hot_model.transform(train_y)
net = Net(30, 50, 2)
我们在Net类中加入一个__mse_list列表,每隔一段迭代便保存当前的最小均方误差;同时我们定义了下面几个函数:
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(y):
return y * (1 - y)
def relu(x):
x[x < 0] = 0
return x
def deriv_relu(y):
y[y > 0] = 1
return y
def leaky(x):
x[x < 0] = 0.1 * x[x < 0]
return x
def deriv_leaky(x):
x[x <= 0] = 0.1
x[x > 0] = 1
return x
def tanh(x):
return np.tanh(x)
def deriv_tanh(y):
return 1 - y**2
分别对应四种激活函数及其导数,我们让四种不同中间层激活函数的神经网络对相同的训练集进行学习50000轮,之所以那么多轮是因为训练使用累积BP,采用批处理机制会减少训练轮数。在训练结束后,使用测试集对四种模型进行测试。结果如下:
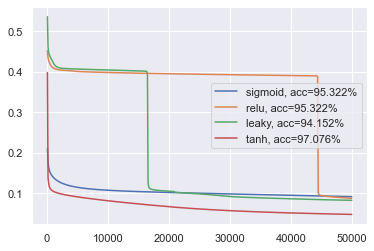
- 表现最佳的是$\tanh$,有更快的收敛速度,验证了前面“以零为中心的激活函数会带来更快的收敛速度”的说法。
- ReLU函数族都伴随着误差突降的现象,相比来说,Sigmoid和$\tanh$要平滑得多;笔者认为是由于ReLU和Leaky ReLU都是带有尖点(也就是不连续点)的函数,因此带来了误差上的突变。
- 与ReLU相比,Leaky ReLU确实更好,体现在误差突变的更早,是否归咎于其不连续点的斜率突变程度要比ReLU要小?有待探究。
总结
我们在这里主要介绍了几种激活函数以及实验观察其在单隐层神经网络中的表现,但得到的结论有限,比如我们没有见识到在层数增加的情况下,ReLU函数族相较于Sigmoid和$\tanh$的优势,这些需要我们构建出多层反向传播网络后才可以一探究竟。