引言
$\text{BP}$算法是当今神经网络的核心,虽然Geoffrey Hinton表示自己对于反向传播「非常怀疑」,并提出「应该抛弃它并重新开始」,但它仍占据绝对地位,本文是作者在实现单隐层神经网络时所作的公式推导的总结,希望从各种方向拓展神经网络的用法,包括层数和激活函数。
基本的单隐层BP算法
我们在实现单隐层神经网络已经详细介绍了神经网络的BP算法的计算方法,在此不过多赘述。
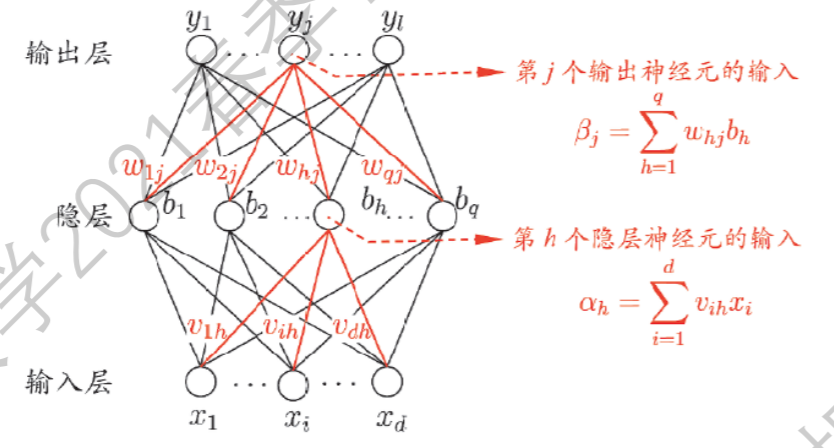
我们这里重新定义一下符号:设输入层神经元$d$,隐层神经元$q$个,输出层神经元$l$个;于是设输入层第$i$个神经元到隐层第$h$个神经元的权重为$v_{ih}$,隐藏层第$h$个神经元到输出层第$j$个神经元的权重为$w_{hj}$,隐藏层第$h$个神经元处的$\text{bias}$为$\gamma_h$,输出层第$j$个神经元的$\text{bias}$为$\theta_j$. 从而我们有第$h$个隐层神经元的输入:
\[\alpha_h=\sum_{i=1}^dv_{ih}x_i\]第$j$个输出层神经元的输入:
\[\beta_j=\sum_{h=1}^qw_{hj}b_h\]其中
\[b_h=\text{sigmoid}(\alpha_h-\gamma_h)\]对于一个给定的数据$(\pmb x,\pmb y)$,我们需要对其平方误差进行求导:
\[\begin{aligned} E&=\dfrac{1}{2}\|\hat{y}-y\|^2_2\\ \dfrac{\partial E}{\partial w_{hj}}&=\dfrac{\partial E}{\partial\hat{y}_j}\cdot\dfrac{\partial\hat{y}_j}{\partial\beta_j}\cdot\dfrac{\partial\beta_j}{\partial w_{hj}}\\ &=(\hat{y}_j-y_j)\cdot\hat{y}_j(1-\hat{y}_j)\cdot b_h \end{aligned}\]这里因为(下面的$f$就是$\text{logisitic}$函数)
\[\hat{y}_j=\text{logisitic}(\beta_j-\theta_j)\\ \dfrac{\mathrm{d}}{\mathrm{d}x}f(x)=f(x)(1-f(x))\]接下来是输出层的偏置更新:
\[\begin{aligned} \dfrac{\partial E}{\partial\theta_j}&=\dfrac{\partial E}{\partial\hat{y}_j}\cdot\dfrac{\partial\hat{y}_j}{\partial\theta_j}\\ &=(\hat{y}_j-y_j)\cdot\dfrac{\partial\hat{y}_j}{\partial(\beta_j-\theta_j)}\cdot\dfrac{\partial(\beta_j-\theta_j)}{\partial\theta_j}\\ &=-(\hat{y}_j-y_j)\cdot\hat{y}_j(1-\hat{y}_j) \end{aligned}\]可以发现$w_{hj}$和$\theta_j$对应的偏导都有共同项$(\hat{y}_j-y_j)\cdot\hat{y}_j(1-\hat{y}_j)$,因此我们设$g_j=\hat{y}_j(1-\hat{y}_j)({y}_j-\hat{y}_j)$,梯度更新时就可以简写为
\[\begin{cases} \Delta{w_{hj}}=-\eta\dfrac{\partial E}{\partial w_{hj}}=\eta g_jb_h\\ \Delta{\theta_j}=-\eta\dfrac{\partial E}{\partial\theta_j}=-\eta g_j \end{cases}\]然后向前一层,也就是输入到隐层的权重和隐层偏置,类似的,我们进行求导:
\[\begin{aligned} \dfrac{\partial E}{\partial v_{ih}} &=\dfrac{\partial E}{\partial\alpha_h}\cdot\dfrac{\partial\alpha_h}{\partial v_{ih}}\\ &=\dfrac{\partial E}{\partial b_h}\cdot\dfrac{\partial b_h}{\partial\alpha_h}\cdot\dfrac{\partial\alpha_h}{\partial v_{ih}}\\ &=\dfrac{\partial}{\partial b_h}\bigg(\dfrac{1}{2}\sum_{j=1}^l(\hat{y}_j-y_j)^2\bigg)\cdot\dfrac{\partial b_h}{\partial\alpha_h}\cdot\dfrac{\partial\alpha_h}{\partial v_{ih}}\\ &=\bigg(\sum_{j=1}^l(\hat{y}_j-y_j)\dfrac{\partial\hat{y}_j}{\partial b_h} \bigg)\dfrac{\partial b_h}{\partial\alpha_h}\cdot\dfrac{\partial\alpha_h}{\partial v_{ih}}\\ &=\bigg(\sum_{j=1}^l(\hat{y}_j-y_j)\dfrac{\partial\hat{y}_j}{\partial\beta_j}\cdot\dfrac{\partial\beta_j}{\partial b_h}\bigg)\dfrac{\partial b_h}{\partial\alpha_h}\cdot\dfrac{\partial\alpha_h}{\partial v_{ih}}\\ &=\dfrac{\partial b_h}{\partial\alpha_h}\cdot\dfrac{\partial\alpha_h}{\partial v_{ih}}\cdot\bigg(\sum_{j=1}^l(\hat{y}_j-y_j)\dfrac{\partial\hat{y}_j}{\partial\beta_j}\cdot\dfrac{\partial\beta_j}{\partial b_h}\bigg)\\ &=b_h(1-b_h)\cdot x_i\bigg( \sum_{j=1}^l(\hat{y}_j-y_j)\hat{y}_j(1-\hat{y}_j)\cdot w_{hj}\bigg)\\ &=b_h(1-b_h)\cdot x_i\bigg(\sum_{j=1}^l-g_jw_{hj}\bigg)\\ &=-b_h(1-b_h)\cdot x_i\bigg(\sum_{j=1}^lg_jw_{hj}\bigg)\\ \end{aligned}\]加下来是隐藏层权重$\gamma_h$:
\[\begin{aligned} \dfrac{\partial E}{\partial\gamma_h}&=\dfrac{\partial E}{\partial b_h}\cdot\dfrac{\partial b_h}{\partial v_{ih}}\\ &=\dfrac{\partial}{\partial b_h}\bigg(\dfrac{1}{2}\sum_{j=1}^l(\hat{y}_j-y_j)^2\bigg)\cdot\dfrac{\partial b_h}{\partial \gamma_h}\\ &=\bigg(\sum_{j=1}^lg_jw_{hj}\bigg)\cdot b_h(1-b_h)\\ \end{aligned}\]可以发现$v_{ih}$和$\gamma_{h}$有共同项$(\sum_{j=1}^lg_jw_{hj})b_h(1-b_h)$,因此设
\[e_h=\bigg(\sum_{j=1}^lg_jw_{hj}\bigg)\cdot b_h(1-b_h)\]从而得到它们的梯度调整项:
\[\begin{cases} \Delta{v_{ih}}=\eta e_hx_i\\ \Delta\gamma_h=-\eta e_h \end{cases}\]至此我们已经完成单隐层神经网络BP算法的推导。
如何支持其他激活函数
我们发现,在前面求偏导的过程中,由于Sigmoid函数满足
\[f'(x)=f(x)(1-f(x))\]的关系,因此$e$和$g$中都有明显的$x(1-x)$的项,类似的,对于$\tanh$函数:
\[\tanh(x)=\dfrac{x^x-e^{-x}}{e^x+e^{-x}}\]其函数与导函数之间满足
\[f'(x)=1-f(x)^2\]我们只需要对$g$和$e$修改成:
\[\begin{aligned} g_j&=(1-\hat{y}_j^2)({y}_j-\hat{y}_j)\\ e_h&=\bigg(\sum_{j=1}^lg_jw_{hj}\bigg)\cdot (1-b_h^2) \end{aligned}\]