引言
我们这里介绍libSVM中的非接口函数,还是下面的结构层次图:
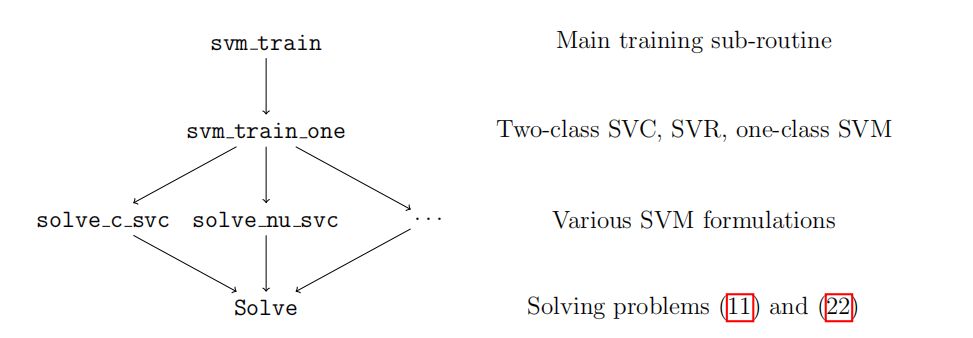
我们已经在前面介绍了Solve类,现在介绍上面的函数。
求解具体问题
libSVM中有五个求解具体SVM问题的函数:
solve_c_svc;solve_nu_svc;solve_one_class;solve_epsilon_svr;solve_nu_svr;
分别对应五种问题(见支持向量机 - 种类汇总),但都要借助基础的Solver类实现。这些函数都用static关键字修饰,因此无法被模块外直接调用。先看solve_c_svc:
static void solve_c_svc(const svm_problem *prob, const svm_parameter *param,
double *alpha, Solver::SolutionInfo *si, double Cp,
double Cn) {
int l = prob->l;
double *minus_ones = new double[l];
schar *y = new schar[l];
int i;
for (i = 0; i < l; i++) {
alpha[i] = 0;
minus_ones[i] = -1;
if (prob->y[i] > 0)
y[i] = +1;
else
y[i] = -1;
}
Solver s;
s.Solve(l, SVC_Q(*prob, *param, y), minus_ones, y, alpha, Cp, Cn,
param->eps, si, param->shrinking);
double sum_alpha = 0;
for (i = 0; i < l; i++)
sum_alpha += alpha[i];
if (Cp == Cn)
info("nu = %f\n", sum_alpha / (Cp * prob->l));
for (i = 0; i < l; i++)
alpha[i] *= y[i];
delete[] minus_ones;
delete[] y;
}
在正式求解之前,函数会初始化参数和规范化数据,比如将$\alpha$设置为零向量,将$p$设置为全-1向量(就是minus_one);而对于数据中的标签$y$,由于外部数据有时会用0和1区分正负类,因此将其映射到$\{-1,+1\}$。在求解完成后,实际上输出的$\alpha$是$\begin{bmatrix}\alpha_i y_i\end{bmatrix}_{1\times l}$,这样设计是为了方便决策函数的表达:
struct decision_function {
double *alpha;
double rho;
};
这样就不需要多出一个成员schar *y来存储$y_i$,同时减少计算量。solve_nu_svc、solve_one_class的流程与solve_c_svc大致相同,区别就在于初始条件的设置和多出一些参数。还剩下两个回归问题,我们来看solve_epsilon_svr:
static void solve_epsilon_svr(const svm_problem *prob,
const svm_parameter *param, double *alpha,
Solver::SolutionInfo *si) {
int l = prob->l;
double *alpha2 = new double[2 * l];
double *linear_term = new double[2 * l];
schar *y = new schar[2 * l];
int i;
for (i = 0; i < l; i++) {
alpha2[i] = 0;
linear_term[i] = param->p - prob->y[i];
y[i] = 1;
alpha2[i + l] = 0;
linear_term[i + l] = param->p + prob->y[i];
y[i + l] = -1;
}
Solver s;
s.Solve(2 * l, SVR_Q(*prob, *param), linear_term, y, alpha2, param->C,
param->C, param->eps, si, param->shrinking);
double sum_alpha = 0;
for (i = 0; i < l; i++) {
alpha[i] = alpha2[i] - alpha2[i + l];
sum_alpha += fabs(alpha[i]);
}
info("nu = %f\n", sum_alpha / (param->C * l));
delete[] alpha2;
delete[] linear_term;
delete[] y;
}
注意到这里我们需要长度为$2l$的数组存储$\alpha$和$\alpha^\star$,然后在长度为$l$的向量中填入的是$\alpha-\alpha^\star$。solve_nu_svr与之类似,不过多赘述。
单次训练
svm_train_one负责训练一次支持向量机并输出结果(一个decision_function),它根据传入参数指定的SVM种类进行指定的求解:
switch (param->svm_type) {
case C_SVC:
solve_c_svc(prob, param, alpha, &si, Cp, Cn);
break;
case NU_SVC:
solve_nu_svc(prob, param, alpha, &si);
break;
case ONE_CLASS:
solve_one_class(prob, param, alpha, &si);
break;
case EPSILON_SVR:
solve_epsilon_svr(prob, param, alpha, &si);
break;
case NU_SVR:
solve_nu_svr(prob, param, alpha, &si);
break;
}
然后计算出支持向量个数和到达边界的支持向量个数:
int nSV = 0;
int nBSV = 0;
for (int i = 0; i < prob->l; i++) {
if (fabs(alpha[i]) > 0) {
++nSV;
if (prob->y[i] > 0) {
if (fabs(alpha[i]) >= si.upper_bound_p) ++nBSV;
} else {
if (fabs(alpha[i]) >= si.upper_bound_n) ++nBSV;
}
}
}
最后将计算结果返回:
decision_function f;
f.alpha = alpha;
f.rho = si.rho;
return f
可以说流程十分简单。
多分类下的分布估计
libSVM提供了sigmoid_train,sigmoid_predoct和multiclass_probablity以及svm_binary_svc_probability负责分类问题的分布估计任务。从这里我们了解到我们要利用已知样本对下式极大似然估计出参数$A$和$B$:
libSVM在sigmoid_train中采用“带回溯的牛顿法”去求解这个优化问题(留坑)。而sigmoid_predict就是在已求出参数的情况下对$r_{ij}$进行估计:
static double sigmoid_predict(double decision_value, double A, double B) {
double fApB = decision_value * A + B;
// 1-p used later; avoid catastrophic cancellation
if (fApB >= 0)
return exp(-fApB) / (1.0 + exp(-fApB));
else
return 1.0 / (1 + exp(fApB));
}
这里一个有趣的手法就是对$Af+B$的值进行讨论,如果非负,则返回
\(\dfrac{\exp (-Af-B)}{1+\exp (-Af-B)}\)
否则按原式计算,这样设计的目的应该是防止指数爆炸带来的数据溢出。在将所有的$r_{ij}$求出来后,便是对类别分布$[p_i]$的估计,也就是论文中提到的概率估计迭代算法,这一算法由multiclass_probability函数来计算。而svm_binary_svc_probability先做交叉验证,然后用决策值来做概率估计,需要调用sigmoid_train函数。
回归问题的噪声估计
svm_svr_probablity函数先用五折交叉验证校准误差,然后以拉普拉斯分布为先验分布,对误差进行最大似然估计。
多分类数据整理
svm_group_classes函数允许多达16类的数据输入,然后对这些数据进行整理和排序:按不同类数据在数据集中第一次出现的顺序作为类别顺序;将同类数据排在一起,并给出其在数据集中的起始点和数量。这样处理显然是为了后续训练的方便。
至此,libSVM只剩下一些接口函数未被提及,这些函数被用户调用,可以用机器学习的步骤去总结。