引言
SVM可以在不提供先验概率的情况下对标签数据(和分类任务中的目标值)进行分布估计,我们这里简单介绍这些问题的思路以及libSVM中相应的算法。
k分类问题的概率估计
给定共$k$类数据,对于任意数据$\pmb x$,我们的目标是估计出
\[p_i=\Pr(y=i\vert\pmb x),i=1,\cdots,k\]我们用“一对一”的方法,先估计成对概率:
\[r_{ij}\approx\Pr(y=i\vert y=i\text{ or }j,\pmb x)\]我们做出假设,$r_{ij}$可以写成如下形式:
\[r_{ij}\approx\dfrac{1}{1+\exp(A\hat{f}+B)}\]其中:
\[\hat{f}=f(\pmb x)=\sum_{i=1}^l\alpha_iy_i K(\pmb x_i,\pmb x)+b\]然后我们利用基于训练数据的极大似然估计法,估计出参数$A$和$B$。由于会过拟合,因此libSVM会先采用5折交叉验证去获取$\hat{f}$。
在得到所有的$r_{ij}$后,我们便着手寻找一组能够最契合$r_{ij}$的概率分布$[p_1,p_2,\cdots,p_k]$,这相当于求解下面的优化问题:
\[\begin{aligned} \min_{\pmb p}\quad&\dfrac12\sum_{i=1}^k\sum_{j:j\neq i}(r_{ji}p_i-r_{ij}p_j)^2\\ \text{subject to}\quad&p_i\ge0,\forall i\\ &\sum_{i=1}^kp_i=1 \end{aligned}\]该问题基于下面的概率等式(不难证明):
\[\Pr(y=j\vert y=i\text{ or }y=j,\pmb x)\cdot\Pr(y=i\vert\pmb x)=\Pr(y=i\vert y=i\text{ or }y=j,\pmb x)\cdot\Pr(y=j\vert\pmb x)\]接着我们可以将原问题重构成矩阵形式:
\[\min_{\pmb p}\quad\dfrac12\pmb p^\top Q\pmb p\\ Q_{ij}=\begin{cases} \sum_{s:s\neq i}r_{si}^2\quad\text{if }i=j\\ -r_{ji}r_{ij}\quad\quad\text{else} \end{cases}\]可以证明$p_i$非负的约束是冗余的。这样只剩下$\sum p_i=1$的约束,设其对应的拉格朗日乘子为$b$,从而直接写出最优性条件:
\[\begin{bmatrix} Q&\pmb e\\\pmb e^\top&0 \end{bmatrix}\begin{bmatrix} \pmb p\\b \end{bmatrix}=\begin{bmatrix} \pmb 0\\1 \end{bmatrix}\]其中$\pmb e$是$k$维全1向量。除了使用高斯消去法去解这个方程组,我们也可以使用普通的迭代法,以更好地在计算机上解决。由
\[\begin{aligned} Q\pmb{p}+b\pmb e&=0\\ -\pmb{p}^\top Qp&=b\pmb{p}^\top\pmb e\\ &=b \end{aligned}\]从而最优解$\pmb p$满足
\[(Q\pmb{p})_t-\pmb{p}^\top Q\pmb{p}=Q_{tt}p_t+\sum_{j:j\neq t}Q_{tj}p_j-\pmb{p}^\top Q\pmb{p}\]我们根据这个等式提出得到$\pmb p$的迭代算法:
-
随机初始化$p_i$,满足$p_1\ge0$,$\sum p_i=1$;
-
按照$1,2,\cdots,k,1,\cdots$的顺序去进行如下操作:
\[\begin{aligned} p_i\gets&\dfrac{1}{Q_{tt}}\big[-\sum_{j:j\neq t}Q_{tj}p_j+\pmb p^\top Q\pmb p \big]\\ \pmb p\gets&\dfrac{1}{\sum p_i}\pmb p\quad(\text{normalization}) \end{aligned}\] -
如果$\pmb p$满足上述矩阵方程,则停止迭代。
注:我们可将$p_i$的迭代和$\pmb p$的规范化进行融合:
\[p_i\gets p_i+\dfrac1{Q_{tt}}\big[-(Q\pmb p)_t+\pmb p^\top Q\pmb p \big]\]考虑到迭代终止条件过于严苛,我们提出一个收敛阈值:
\[\Vert Q\pmb p-\pmb p^\top Q\pmb{pe}\Vert_\infty=\max_{t}\vert(Q\pmb p)_t-\pmb p^\top Q\pmb p\vert\lt0.005/k\]利用$k$来控制收敛。
回归问题的噪声估计
我们假定数据集$\mathcal{D}$是从下面的模型采集得来:
\[y_i=f(\pmb x_i)+\delta_i\]其中$f(\pmb x)$是潜在的未知函数,$\delta_i$来自一个独立同分布的随机噪声。给定测试数据$\pmb x$,我们希望估计出$\Pr(y\vert\pmb x,\mathcal{D})$,从而完成一些概率分布相关任务,比如区间估计:估计出
\[y\in[f(\pmb x)-\Delta,f(\pmb x)+\Delta]\]的概率。我们设$\hat f$为SVR对训练集$\mathcal{D}$学习后得到的拟合函数,然后设$\zeta=\zeta(\pmb x)\equiv y-\hat{f}(\pmb x)$为预测误差。这里需要用交叉验证来减小偏差使得$\zeta_i$更准确。根据实验得到下面的直方图:
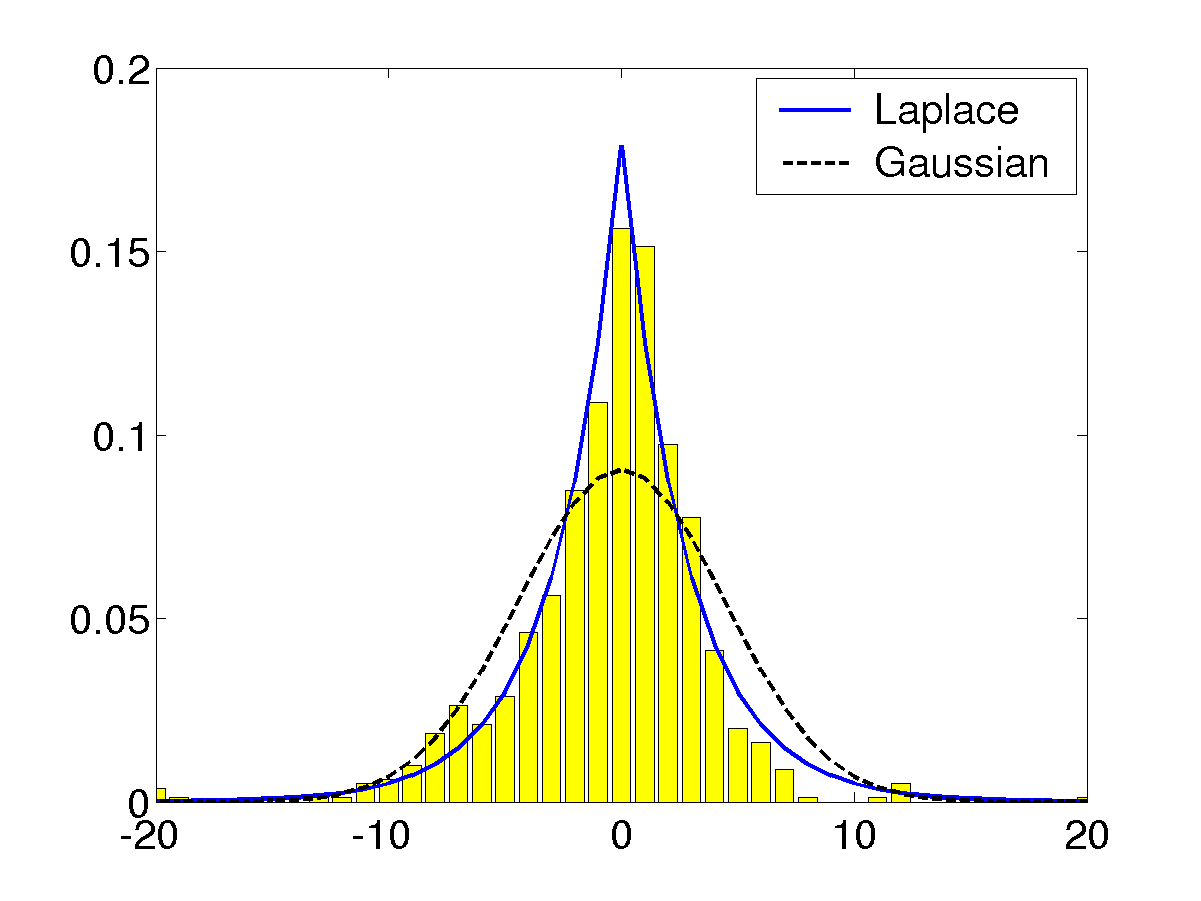
libSVM采用零均值的拉普拉斯分布来拟合误差:
\[p(z)=\dfrac{1}{2\sigma}\exp(-\dfrac{\vert z\vert}{\sigma})\]其中的参数$\sigma$可以利用极大似然法去估计:
\[\sigma=\dfrac{\sum_{i=1}^l\vert\zeta_i\vert}{l}\]于是我们有
\[y=\hat{f}(\pmb x)+z\]其中$z$是满足参数为$\sigma$的拉普拉斯分布。