引言
我们会在这里介绍总共五种支持向量机,分别用于分类、回归和分布估计任务。
C-SVC
C-SVC,也就是$C$-Support Vector Machine, 是最简单的二分类支持向量机

其实是解决下面的优化问题:
\[\begin{aligned} \min_{\pmb w,b,\pmb\xi}\quad&\dfrac12\Vert\pmb w\Vert^2+C\sum_{i=1}^l\xi_i\\ \text{subject to}\quad&y_i(\pmb w^\top\phi(x_i)+b)\geqslant1-\xi_i\\ &\xi_i\geqslant 0,i=1,\cdots,l \end{aligned}\]我们也不难得到其对应的对偶问题:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^\top Q\pmb\alpha-\pmb{e}^\top\pmb{\alpha}\\ \text{subject to}\quad& \pmb{y}^\top\alpha=0,\\ &0\leqslant\alpha_i\leqslant C,i=1,\cdots ,l \end{aligned}\]其中$Q$是一个全1向量,而$Q_{ij}=y_iy_jK(\pmb x_i,\pmb x_j)=y_iy_j\phi(\pmb x_i)^\top\phi(\pmb x_j)$。当我们解决了上面的对偶问题后,我们就可以得到$\pmb w$的解:
\[\pmb w=\sum_{i=1}^ly_i\alpha_i\phi(\pmb x_i)\]从而决策函数:
\[\text{sgn}(\pmb w^\top\phi(\pmb x)+b)=\text{sgn}\bigg(\sum_{i=1}^ly_i\alpha_i K(x_i,x)+b\bigg)\]$\varepsilon$-SVR
$\varepsilon$-SVR,也就是$\varepsilon$-Support Vector Regression,是利用支持向量机来解决回归问题:
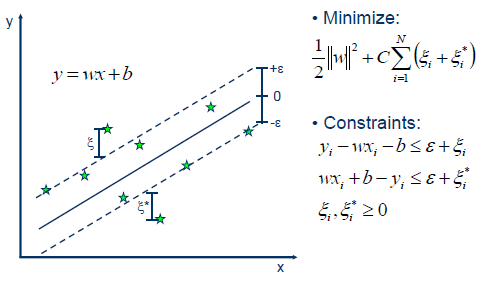
实际的优化问题已经在上图写出,而其对偶问题为:
\[\begin{aligned} \min_{\pmb{\alpha},\pmb{\alpha}^*}\quad&\dfrac12(\pmb{\alpha}-\pmb{\alpha}^*)^\top Q(\pmb{\alpha}-\pmb{\alpha}^*)+\varepsilon\sum_{i=1}^l(\alpha_i+\alpha_i^*)+\sum_{i=1}^l z_i({\alpha}_i-{\alpha}_i^*)\\ \text{subject to}\quad&\pmb e^\top(\pmb{\alpha}-\pmb{\alpha}^*)=0\\ &0\leqslant\alpha_i,\alpha^*_i\leqslant C,i=1,\cdots ,l \end{aligned}\]这里的$z_i$是对应数据的输出,如此设置是为了不和分类问题中的标签$y_i$混淆。
这里$Q_{ij}=K(x_i,x_j)$。当我们求出该对偶问题后,也就能得到拟合函数
\[z(\pmb x)=\sum_{i=1}^l(-\alpha_i+\alpha_i^*)K(\pmb{x}_i,\pmb x)+b\]$\nu$-SVC
$\nu$-Support Vector Classification在前面的$C$-SVC基础上引入了一个新参数$\nu$,用以控制训练误差和支持向量的数量:
\[\begin{aligned} \min_{\pmb w,b,\pmb\xi,\rho}\quad&\dfrac12\Vert\pmb w\Vert^2-\nu\rho+\dfrac1l\sum_{i=1}^l\xi_i\\ \text{subject to}\quad&y_i(\pmb w^\top\phi(\pmb x_i)+b)\geqslant\rho-\xi_i\\ &\xi_i\geqslant0,i=1,\cdots,l\\&\rho\geqslant 0 \end{aligned}\]对应的对偶问题:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\dfrac12\pmb\alpha^\top Q\pmb\alpha\\ \text{subject to}\quad&0\leqslant\alpha_i\leqslant\frac{1}{l},,i=1,\cdots,l\\ &\pmb{e}^\top\pmb\alpha\geqslant \nu,\pmb y^\top\pmb{\alpha}=0 \end{aligned}\]可以把它和$C$-SVC 的对偶问题进行比较,发现框架大体相同,$\nu$其实是对$\pmb e^\top\pmb\alpha$进行了限制。两种SVC问题的决策函数是相同的。
$\nu$-SVR
类似的,$\nu$-Support Vector Regression是将$\nu$引入$\varepsilon$-SVR,它解决的是一个优化问题:
\[\begin{aligned} \min_{\pmb x,b,\pmb\xi,\pmb\xi^*,\varepsilon}\quad&\dfrac12\Vert\pmb w\Vert^2+C\big(\nu\varepsilon+\frac1l\sum_{i=1}^l(\xi_i+\xi^*_i)\big)\\ \text{subject to}\quad&(\pmb w^\top\phi(\pmb x_i)+b)-z_i\leqslant\varepsilon+\xi_i\\ &z_i-(\pmb w^\top\phi(\pmb x_i)+b)\leqslant\varepsilon+\xi_i^*\\ &\xi_i,\xi^*\geqslant0,i=1,\cdots,l\\ &\varepsilon\geqslant0 \end{aligned}\]发现约束条件与$\varepsilon$-SVR差别不大,其对偶问题:
\[\begin{aligned} \min_{\pmb{\alpha},\pmb{\alpha}^*}\quad&\dfrac12(\pmb{\alpha}-\pmb{\alpha}^*)^\top Q(\pmb{\alpha}-\pmb{\alpha}^*)+\pmb z^\top({\pmb\alpha}-{\pmb\alpha}^*)\\ \text{subject to}\quad&\pmb e^\top(\pmb{\alpha}-\pmb{\alpha}^*)=0,\pmb e^\top(\pmb\alpha+\pmb\alpha_i^*)\leqslant C\nu\\ &0\leqslant\alpha_i,\alpha^*_i\leqslant C/l,i=1,\cdots ,l \end{aligned}\]其解出的近似函数和$\varepsilon$-SVR相同。
One-class SVM
现实中存在这样一个问题,在数据集$X$中判断某个数据$x_i$是不是异常数据,也就是说,对于$x_i$,我们想判断$x_i$与$X\backslash x_i$有多相似,如果相似度低,就将其剔除。可以发现这与分类任务并不完全相同,因为涉及到的类别只有一种。用于处理这一问题的支持向量机被称作One-class SVM。这一过程也被称为分布估计(Distribution estimate)。
One-class SVM的原问题:
\[\begin{aligned} \min_{\pmb w,\pmb\xi,\rho}\quad&\dfrac{1}{2}\Vert\pmb w\Vert^2-\rho+\dfrac{1}{\nu l}\sum_{i=1}^l\xi_i\\ \text{subject to}\quad&\pmb{w}^\top\phi(\pmb x_i)\ge\rho-\xi_i,\\ &\xi_i\geqslant0,i=1,\cdots,l. \end{aligned}\]其对偶问题:
\[\begin{aligned} \min_{\pmb\alpha}\quad&\dfrac{1}{2}\pmb\alpha^\top Q\pmb\alpha\\ \text{subject to}\quad&0\le\alpha_i\le1/(\nu l),i=1,\cdots l\\ &\pmb e^\top\alpha=1 \end{aligned}\]其中$Q_ij=K(x_i,x_j)$,决策函数:
\[\text{sgn}\bigg(\sum_{i=1}^l\alpha_iK(\pmb x_i,\pmb x)-\rho\bigg)\]