引言
我们之前已经通过简单的数学方法求出在选定变量$i$和$j$后对应的$\alpha$分量的更新公式:
\[\alpha_i^{k+1}=\alpha_i^k+\dfrac{y_i}{\eta}(E_j-E_i)\\ \alpha_j^{k+1}=\alpha_j^k+\dfrac{y_j}{\eta}(E_i-E_j)\]这种写法是抽象的,难以通过程序实现;而我们已经知道了LIBSVM中如何筛选出合适的变量,我们希望通过利用我们在筛选变量时得到的结论和变量(及其符号),继续推导出$\alpha$的更完备的更新公式,从而与上式形成闭环。同时补充剪辑算法。
LIBSVM中更新$\alpha$
我们在选择变量时提到,我们选择$x_j$时希望能让
\[f(\alpha^k+d)-f(\alpha^k)\]越小越好,那么我们自然会做出如下的变量更新:
\[\begin{cases} \alpha_i^{k+1}=\alpha_i^k+d_i=\alpha_i^k+y_i\dfrac{b_{ij}}{a_{ij}}\\ \alpha_j^{k+1}=\alpha_j^k+d_j=\alpha_j^k-y_j\dfrac{b_{ij}}{a_{ij}} \end{cases}\tag{*}\]我们已经知道$\eta=a_{ij}$,而若我们想证明两种更新方式是等价的,也就是证明:
\[b_{ij}=E_j-E_i\]我们对等式两边进行展开:
\[\begin{aligned} -y_i\nabla f(\alpha)_i+y_j\nabla f(\alpha)_j&=\sum_{k=1}^m\alpha_ky_kK_{kj}+b-y_j-\sum_{k=1}^m\alpha_ky_kK_{ki}-b+y_i\\ &=-y_i(\sum_{k=1}^m\alpha_ky_ky_iK_{ki}-1)+y_j(\sum_{k=1}^m\alpha_ky_ky_jK_{kj}-1)\\ &=-y_i\nabla f(\alpha)_i+y_j\nabla f(\alpha)_j \end{aligned}\]从而证明两种迭代公式的等价性。但我们想要更精细地求解,因此抛弃《统计学习方法》中粗略的$E_1-E_2$的表示法,使用*式来分析。我们将$b_{ij}$用其实际含义替换,发现需要分类讨论:
-
如果$y_i\neq y_j$:
\[\begin{aligned} \alpha_i^{k+1}&=\alpha_i^k+y_i\dfrac{b_{ij}}{a_{ij}}\\ &=\alpha_i^k+\dfrac{-\nabla f(\alpha)_i-\nabla f(\alpha)_j}{a_{ij}}\\ \alpha_j^{k+1}&=\alpha_j^k-y_j\dfrac{b_{ij}}{a_{ij}}\\ &=\alpha_j^k+\dfrac{-\nabla f(\alpha)_i-\nabla f(\alpha)_j}{a_{ij}}\\ \end{aligned}\]定义
\[\delta_{y_i\neq y_j}=\dfrac{-\nabla f(\alpha)_i-\nabla f(\alpha)_j}{a_{ij}}\] -
如果$y_i=y_j$,类似的,我们有
\[\begin{aligned} \alpha_i^{k+1} &=\alpha_i^k-\dfrac{\nabla f(\alpha)_i-\nabla f(\alpha)_j}{a_{ij}}\\ \alpha_j^{k+1}&=\alpha_j^k+\dfrac{\nabla f(\alpha)_i-\nabla f(\alpha)_j}{a_{ij}}\\ \end{aligned}\]定义
\[\delta_{y_i=y_j}=\dfrac{\nabla f(\alpha)_i-\nabla f(\alpha)_j}{a_{ij}}\]
对$\alpha$进行剪辑
我们在前面提到,由于$\alpha_i\in[0,C]$,因此我们在更新时需要将$\alpha$限制在该区间内,该步骤称为剪辑(Clipping),我们在《SMO计算方法》里仅提到了大致流程,这里进行一个深入讲解。
我们只讨论$y_i\neq y_j$的情况,$y_i=y_j$的情况下讨论是类似的。由上面的更新公式,我们有:
\[\alpha_i^{k+1}-\alpha_i^{k}=\alpha_j^{k+1}-\alpha_j^{k}\]此时两变量的状态$(\alpha_i,\alpha_j)$对应左图的虚线(图片摘自《统计学习方法》,这里是将$x_1$作为$x_i$,$x_2$作为$x_j$):
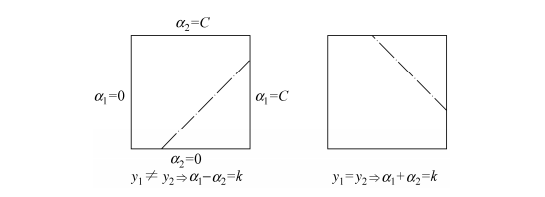
而更一般的情形如下图所示,$\alpha_i\in[0,C_i]$,每个变量的边界不一定相同,常常在类别不平衡的问题中使用:
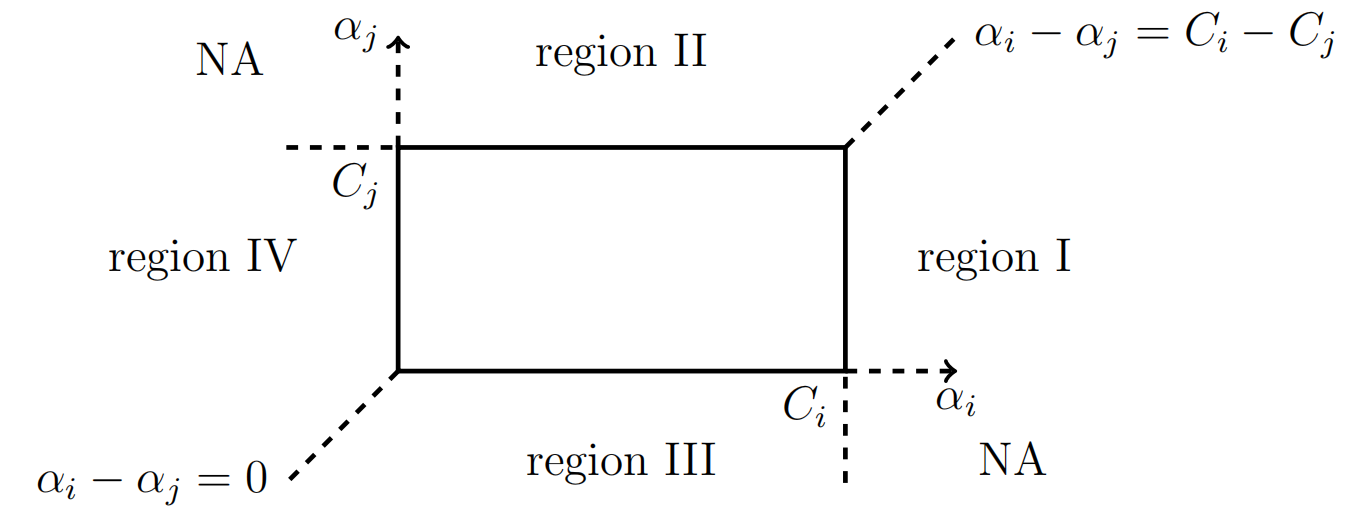
显然$(\alpha_i,\alpha_j)$必须在图中的矩形中,而在更新的过程中,参数对存在跳出矩形区域的可能,也就是Region I到Region IV这四个不合理区域,需要将这些区域的点扳回矩形中;NA则是不可达点,因为$y_i\neq y_j$的情况下参数对只能向左下方或者右上方跳动。
以处于Region I的点为例,此时有
\[\begin{cases} \alpha_i\gt C_i\\ \alpha_i-\alpha_j>C_i-C_j \end{cases}\]我们将$\alpha_i$挪到矩形边缘中,同时保持$\alpha_i$和$\alpha_j$的关系:
\[\begin{cases} \alpha_i^{k+1}=C_i\\ \alpha_j^{k+1}=C_i-(\alpha_i^k-\alpha_j^k) \end{cases}\]同理,对于Region II,我们有
\[\begin{cases} \alpha_i^{k+1}=C_j+\alpha_i^{k}-\alpha_j^k\\ \alpha_j^{k+1}=C_j \end{cases}\]Region III:
\[\begin{cases} \alpha_i^{k+1}=\alpha_i^k-\alpha_j^k\\ \alpha_j^{k+1}=0 \end{cases}\]Region IV:
\[\begin{cases} \alpha_i^{k+1}=0\\ \alpha_j^{k+1}=-(\alpha_i^k-\alpha_j^k ) \end{cases}\]对于$y_i=y_j$的情况有类似的处理方式。