引言
本文是笔者在参加Kaggle月赛,使用模型时调参实验记录,供自己和他人的日后参考。
问题引入
比赛任务是对一个200000条,75个特征,9个类别的有标签数据进行学习,然后对一个100000条的无标签数据集进行预测,然后对数据进行对数损失评估:
\[\text{loss}=-\dfrac{1}{N}\sum_{i=1}^N\sum_{j=1}^M y_{ij}p_{ij}\]我们对上式进行一个解释:我们对测试集进行分类时,是依靠概率进行分类:
\[M=\begin{bmatrix} p_{ij} \end{bmatrix}_{N\times M}\]此问题中$N=100000,M=9$,$p_{ij}$表示第$i$个数据是第$j$类的概率,我们上传的分类结果就是$M$的表格形式;而$y_{ij}$是一个指示器:对于数据$i$,如果分类是正确的,也就是正确答案是$j$类,而你提交的预测结果恰为$j$,也就是预测正确,那么$y_{ij}=1$,否则为$0$:
\[\text{Given }x_i\text{ belongs to class c}:\\ y_{ij}=\begin{cases} 1\qquad\text{if } c=j\\ 0\qquad\text{else} \end{cases}\]所以可以看出$\text{loss}$越小,分类效果越好。我们的任务就是找到$\text{loss}$越小的分类器。
原理浅析
常用的算法有GBDT,随机森林等,我们先使用深度森林模型进行分类,随机森林是一种集成学习方法,由多个决策树构成,用投票法决定输出概率或结果:假设我们有$n$个决策树,对于一个$C$分类问题,$c_i(i=1,2,\cdots,n)$表示第$i$棵决策树的对数据$\boldsymbol{x}$的分类结果,从而对于整个随机森林,$\boldsymbol{x}$是第$c$类的概率:
\[\Pr(\boldsymbol{x}\in c)=\dfrac{1}{n}\sum_{i=1}^n\mathbb{I}(c_i=c)\]其中$\mathbb{I}(p)$是一个指示器函数:如果$p$命题为真则函数值为$1$,否则为$0$.
代码书写
我们通常使用scikit-learn中的RandomForestClassifier模块进行深度森林模型的实现:
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
# We don't mention how to read and process data here
model = RandomForestClassifier()
model.fit(train_x, train_y)
proba = model.predict_proba(test_x.values)
output = pd.DataFrame({
'id': test_x.index,
'Class_1': proba[:, 0],
'Class_2': proba[:, 1],
'Class_3': proba[:, 2],
'Class_4': proba[:, 3],
'Class_5': proba[:, 4],
'Class_6': proba[:, 5],
'Class_7': proba[:, 6],
'Class_8': proba[:, 7],
'Class_9': proba[:, 8],
})
output.id += 200000 # In order to satisfy format required by kaggle
output.to_csv("my_submission.csv", index=False)
第一次提交
然后我们去官网提交观察结果:

$\text{loss}$是2.01416,什么水平呢?截止到6月11日,第一名的成绩是1.74403,作为参考,比赛方设计了一个基准:$p_{ij}$都是$0.1111$,也就是$\dfrac{1}{9}$,即随机猜测,它的分数是2.19722,说明我们还差的很远。
由于每天只能提交五次(防止恶意提交),我们必须得自己设计评估函数,将给定的测试数据进训练,测试和评估,选定最合适的参数后训练再提交。
设计完整的任务流程
我们首先得对有标签数据集划分成训练集和测试集:
def data_split(path="train.csv", frac=0.8):
# 根据path获取数据
# 随机打乱数据(shuffle)
# 定义bound
bound = int(data_len * frac)
# 划分
df_train = df.iloc[:bound]
df_test = df.iloc[bound:]
return (
df_train.iloc[:, :-1], # 训练集特征向量
df_train['target'], # 训练集标签
df_test.iloc[:, :-1], # 测试集特征向量
df_test['target'], # 测试集标签
)
在训练模型后,我们需要对已有模型进行评估(estimate),为此我们定义一个estimate函数,计算对应的loss:
from numpy as np
from sklearn.preprocessing import OneHotEncoder
def evaluation(result, test_y):
result = result.values
test_y_array = test_y.values.reshape(-1, 1)
result[result == 0.0] = 0.0000001
enc = OneHotEncoder()
enc.fit(test_y_array)
y = enc.transform(test_y_array).toarray()
loss = -np.sum(np.log(result) * y) / result.shape[0]
return loss
值得注意的是,我们将概率预测为$0$的$p_{ij}$项改成极小的0.0000001,是为了在后面的对数运算中避免$\log0$的异常,我们相信在kaggle的判定程序中也有类似的处理,但惩罚可能比较大。这一函数也为后面的调参环节提供数值依据。
参数的设计与选取
到这里,我们需要思考的是,可以控制的参数有哪些,这些参数的变化会对模型的性能产生什么影响,以及如何观察。
一个简单的例子
我们先从最简单的参数:分割训练集和测试集的比例(frac)开始,我们将其分为0.1, 0.2, …, 0.9,观察损失函数:(前提是控制变量)
import matplotlib.pyplot as plt
import seaborn as sns
loss_lost = []
for i in range(1, 10):
frac = i / 10
loss_sum = 0
for j in range(4):
train_x, train_y, test_x, test_y = data_split(frac=frac)
model = train(train_x, train_y)
output = test(test_x, model)[0]
loss = evaluation(output, test_y)
loss_sum += loss
loss_lost.append(loss_sum / 4)
print("%d iteration is over" % i)
sns.set()
plt.plot(loss_lost)
plt.show()
注意到我们在每个frac中都要进行交叉验证,我们将参数与损失之间的关系通过作图展示:
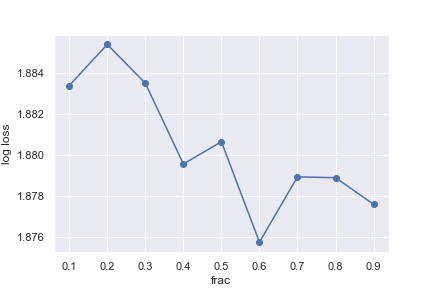
我们发现训练集:测试集为6:4时有最佳效果,我们原本是200000个测试集和100000训练集,所以为了更好的结果,我们选择从训练集中随机提取150000条数据。
学习器的参数
我们更应该考虑的是学习器的参数,所以这一部分主要是观察RandomForestClassifier的参数含义以及对性能的影响。
RF需要调整的参数包括两部分:框架参数和决策树参数,我们来做一个简单介绍。
框架参数
n_estimators:最大的弱学习器,这里也就是决策树的个数。太少会欠拟合,而太大则伴随计算量的增加和模型提升的减小。oob_score:即是否采用袋外样本来评估模型的好坏,默认为False。袋外分数反应了一个模型拟合后的泛化能力。criterion:决策树做划分时的判定标准,默认为gini,表示基尼指数,你也可以选择entropy,表示信息熵增益,一般选择默认的gini。
其中对性能最重要的是n_estimators,也就是最大决策树个数。
决策树参数
- 决策树划分的最大特征数
max_features,默认是auto,表示划分最多考虑$\sqrt{N}$个特征,等价于sqrt,也可以是log2,表示$\log_2N$个特征,如果是整数则是特征的绝对数,浮点数则表示总特征数的百分比,一般用默认参数即可。 - 决策树最大深度
max_depth, 默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。 - 内部节点再划分所需最小样本数
min_samples_split: 这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。 - 叶子节点最少样本数
min_samples_leaf: 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比。如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。 - 叶子节点最小的样本权重和
min_weight_fraction_leaf:这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝。 默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。 - 最大叶子节点数
max_leaf_nodes: 通过限制最大叶子节点数,可以防止过拟合,默认是”None”,即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制,具体的值可以通过交叉验证得到。 - 节点划分最小不纯度
min_impurity_split: 这个值限制了决策树的增长,如果某节点的不纯度(基于基尼系数,均方差)小于这个阈值,则该节点不再生成子节点。即为叶子节点 。一般不推荐改动默认值$1e-7$。 - 类别权重
class_weight:指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多,导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重,或者用“balanced”,如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。当然,如果你的样本类别分布没有明显的偏倚,则可以不管这个参数,选择默认的None。
对我们这个多特征多样本数量的学习任务,我们主要考虑max_features、max_depth、min_sample_split、min_sample_leaf和class_weight。
我们接下来就是对这些参数进行探究。
调参实验
类似于上面的例子,我们通过控制变量队模型参数进行探究。
n_estimators
先来观察n_estimators的数量对学习器性能的影响:
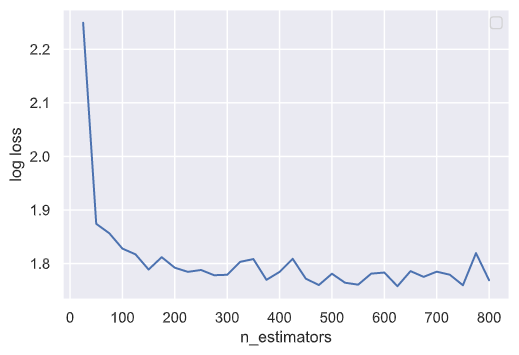
我们在其他参数默认的情况下对不同的n_estimators以25为步长进行测试,测试结果告诉我们,n_estimators的增加确实会带来loss的降低,但当其过大时效果则不是很好。
max_features
我们再来看看max_features对模型性能的影响,我们先来看看默认的auto,也就是$\sqrt{N}$个特征和$\log_2N$的区别,我们尝试用频率来观察效果以避免偶然性:
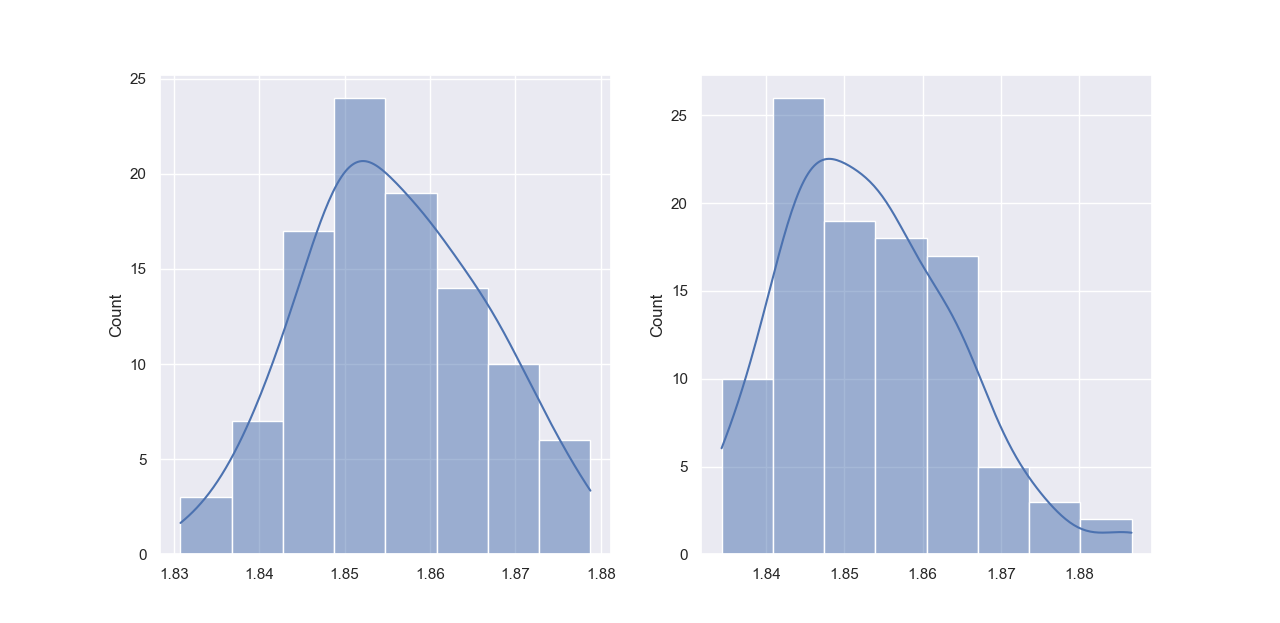
左边是sqrt,右边是log2。从均值上看,显然sqrt要优于log2。
max_depth
我们尝试探究最大深度对学习器的性能的影响,下面是n_estimators分别在100, 200, 500的情况下梯度对对数损失的影响:
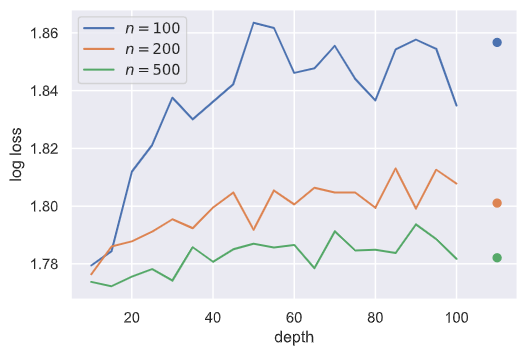
其中最右端的三个点是depth=None情况下的性能,用于参考。可以发现,深度在20附近时,指定深度更优,但随着深度增加,性能往往不如让决策树展开至叶节点。一个合理的解释是,当depth过大,就超过决策树真正的深度,等价于指定depth为None。这一点在n_estimators为500时更明显。
min_sample_split
min_sample_split在我们这个大样本学习任务中应该增大,我们进行探究:
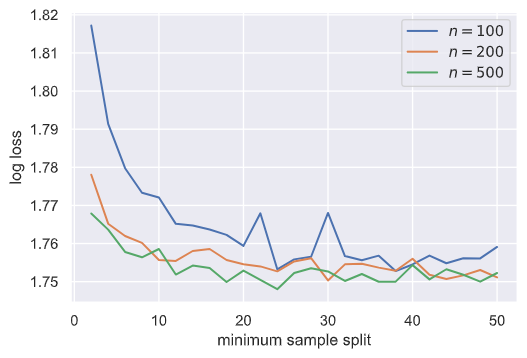
告诉我们将其设置为10到20即可,太大则效果不明显甚至有反效果。
min_sample_leaf
和上面一样,min_sample_leaf在数据量较大的情况下应该增大,我们通过实验来验证这一结论:
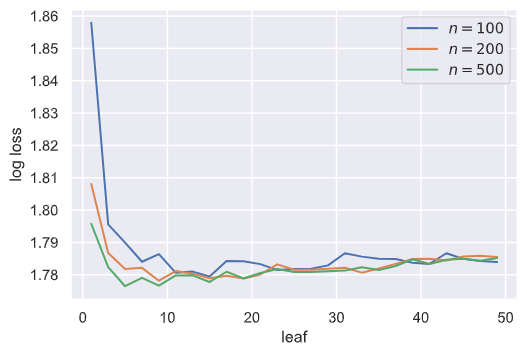
我们发现当min_sample_leaf小于10的时候,性能有较大提高,但在10之后,性能有所下降,可能是叶子节点最少样本数过大会导致分类不彻底。
class_weight
我们会比较设置class_weight为balanced和None的学习器之间的性能区别,通过观察分布:
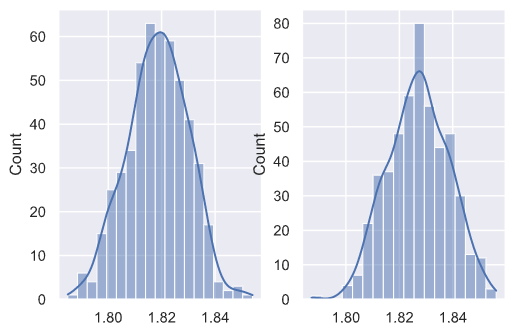
我们发现class_weight设置为balanced确实有助于提升性能。