引言
本文本是没有必要写的,但5月17日早上发生的一系列事情导致我等乐子人无暇听课,详情参考《枕溪本纪》。本文是对习题课上关于PCA内容的整理与复习。
问题引入
在一个正交属性空间的样本点集合中,我们如何使用一个超平面对所有样本进行恰当表达?说起来可能难以理解,我们用下面的图距离,比如我们有个三个特征的样本点集:

它们是没有类别标签的,但我们还是想根据已知数据将这些样本进行分类,这就是一个经典的无监督学习,就像下面这样:
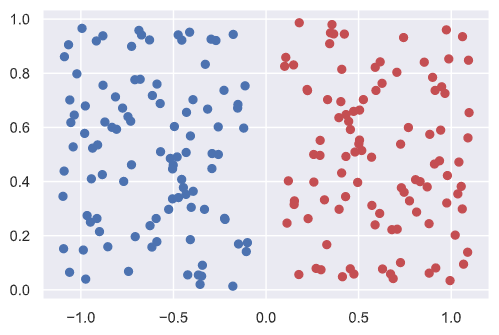
即使图中样本没有标签,我们也可以用肉眼进行分类,而对于多维的数据,比如上面的三维数据,我们可以找到一个平面,将数据投影其上:

这样点集的特征就很鲜明。我们的目标就是找到一个这样的超平面。
问题求解
若存在这样的超平面,那么它大概具有如下性质:
- 最大可分性:样本点在这个超平面上的投影尽可能分开(类比到线性判别分析,这里每个点都是一个类);
- 最近重构性:样本点到这个超平面的距离都足够近。
我们会证明两种推导是等价的。这就是主成分分析($\text{Principal component analysis}$)。在正式求解PCA问题之前,我们先对数据进行中心化:
\[\sum_{i}x_i=0\]我们等下会看到这样操作的原因。
最大可分性
样本点$\pmb x_i$在新空间中超平面上的投影是$\pmb W^\top\pmb x_i$,比如$\pmb x_i$是一个$4$维向量,通过左乘一个矩阵将其变换成一个$2$维向量,也就是投影到一个超平面:
\[(\pmb W_{4\times2})^\top\pmb x_i=\pmb x'_i\]为了让投影尽可能分开,我们应使投影后的方差最大化:
\[\text{maximize }\sum_{i}(\pmb{W}^\top\pmb{x}_i\pmb{x}_i^\top\pmb{W})\]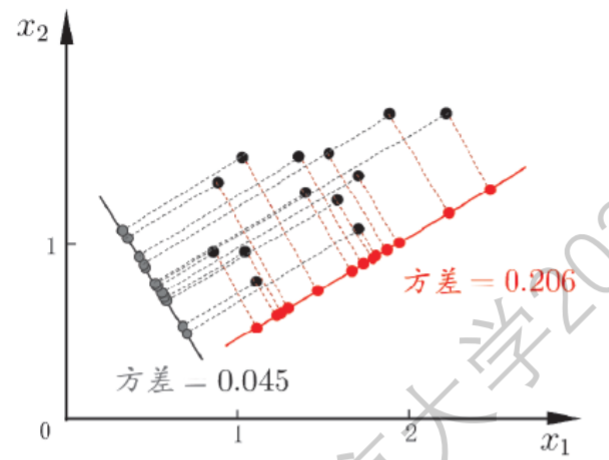
将问题形式化:
\[\begin{aligned} &\text{max }\text{tr}\big(\pmb{W}^\top\pmb{XX}^\top\pmb{W}\big)\\ &\text{s.t. }\pmb{W}^\top\pmb{W}=\mathbf{I} \end{aligned}\]也就是
\[\begin{aligned} &\min_{\pmb W}-\text{tr}\big(\pmb{W}^\top\pmb{\Sigma}\pmb{W}\big)\\ &\text{s.t. }\pmb{W}^\top\pmb{W}=\mathbf{I} \end{aligned}\]
- 这里的$\pmb\Sigma=\pmb{XX}^\top$,就是协方差矩阵,而协方差的定义是$\sum_{i}(x_i-\mu)(x_i-\mu)^\top$,我们之前的中心化其实是简化了该式.
- 这里的$\pmb W$是一个矩阵,根据投影的性质,我们知道$\pmb W$的行数必然大于等于列数;特别的,如果列数为1,矩阵退化为向量,那么会投影到$\mathbb{R}$. 此时上面的迹运算也可以省去。
我们利用拉格朗日乘子法去求解该凸优化问题:
- 构造拉格朗日函数:
- 令$\dfrac{\partial L}{\partial\pmb{W}}=0$:
也就是
\[\pmb\Sigma\pmb{W}=\lambda\pmb{W}\]显然$\pmb{W}_{n\times m}(m\leqslant n)$是实对称矩阵$\pmb\Sigma$的$m$个特征向量排列成的列向量矩阵:
\[\pmb{W}_{n\times m}=\begin{bmatrix} \textbf{v}_1&\cdots&\textbf{v}_m \end{bmatrix},\pmb{\Sigma}\textbf{v}_i=\lambda\textbf{v}_i\]这里我们选择$n$个特征值中最大的$m$个对应的特征向量来组成我们的$\pmb W$,这就是主成分分析(PCA)的解。
最近重构性
假定经过投影变换后得到的新坐标系时$\{\pmb w_1,\pmb w_2,\cdots,\pmb w_n\}$,其中$\pmb w_i$时标准正交基向量:
\[\|\pmb{w}_i\|_2=1,\pmb w_i^\top\pmb w_j=0(i\neq j)\]我们的任务使得我们需要丢其新坐标系的部分坐标,即将维度降到$m\lt n$,则样本点$\pmb x_i$在低维坐标系中的投影是$\pmb z_i=(z_{i1},z_{i2},\cdots,z_{im}),z_{ij}=\pmb w_j\pmb x_i$。如果基于$\pmb z_i$来重构$\pmb{x}_i$,则有
\[\hat{\pmb x}_i=\sum_{j=1}^mz_{ij}\pmb w_j\]原样本点$\pmb x_i$与投影重构后的样本点$\hat{\pmb x}_i$之间距离:
\[\begin{aligned} \sum_{i=1}^n\bigg\|\sum_{j=1}^mz_{ij}\pmb{w}_j-\pmb{x}_i\bigg\|_2^2 &=\sum_{i=1}^n\pmb{z}_i^\top\pmb{z_i}-2\sum_{i=1}^n\pmb{z}_i^\top\pmb{W}^\top\pmb{x}_i+\sum_{i=1}\|\pmb x_i\|^2_2\\ &\propto-\text{tr}\bigg(\pmb{W}^\top\big(\sum_{i=1}^n\pmb{x}_i\pmb{x}_i^\top\big)\pmb{W}\bigg)\\ &=-\text{tr}(\pmb{W}^\top\pmb{XX}^\top\pmb{W}) \end{aligned}\]最近重构性要求上式尽可能小,那么这个优化问题等价于我们在”最大可分性”中提出的问题,进而证明其等价性。
下图是分别用Fisher投影(监督)和PCA(无监督)去降维的效果:
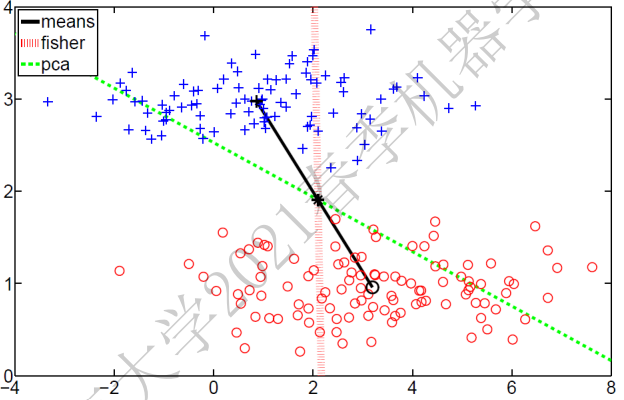
PCA应用
数据的处理
之前我们提到,我们在进行PCA计算前会对数据进行中心化预处理,也就是
\[\sum_{i}\pmb x_i=\pmb 0\]这是为了减少计算的复杂度。除此以外,我们还会对数据进行标准化:
\[\pmb z_i=\dfrac{\pmb x_i-\pmb \mu}{\pmb\sigma}\]这是为了让不同维度的数据尺度相同(身高和体重就是不同的尺度)。
维度的设置
我们将数据从高维降维时,如果维度下降太小,则效果不好;反之则可能丢失一些特征,因此选择好下降的维数时重要的。
一个简单的方法是用户指定,比如在前面,我们想尝试用肉眼去分类无标记样本,那么将数据将至2维并可视化是一个不错的选择;除此以外,我们是否能够想监督学习那样,找到一个欠拟合(类比低维)和过拟合(类比高维)的折中点呢:
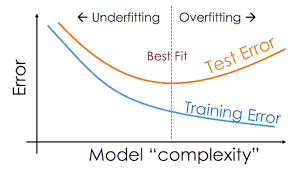
很遗憾,监督学习中的经验不一定在无监督学习中奏效。下图揭示了在PCA这样一个无监督学习任务下,随着模型复杂度上升,测试误差和训练误差的变化趋势:
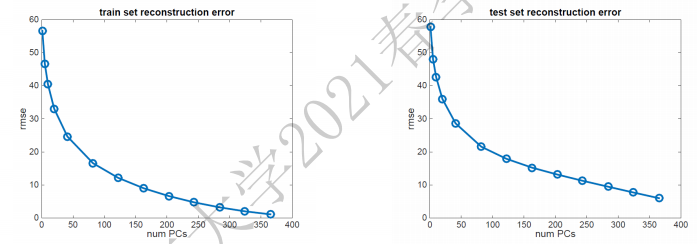
纵轴含义是平均重构误差$\text{rmse}$(Reconstruction mean square loss),度量的是重构后的点与之前位置的欧几里得距离,越小说明“最近重构性”越被满足。
上图告诉我们:维数减少得越多,重构误差越大,意味着一些特征的丢失。因此我们无法通过重构误差和监督模型的误差曲线来寻找最好的模型。
我们可以采用一些启发式方法,比如设置“重构阈值”,我们刚才提到,我们选择几个最大特征值对应的特征向量来作为投影矩阵算子。我们可以设置一个阈值$t=95\%$,然后寻找满足下式的$m$的最小值:
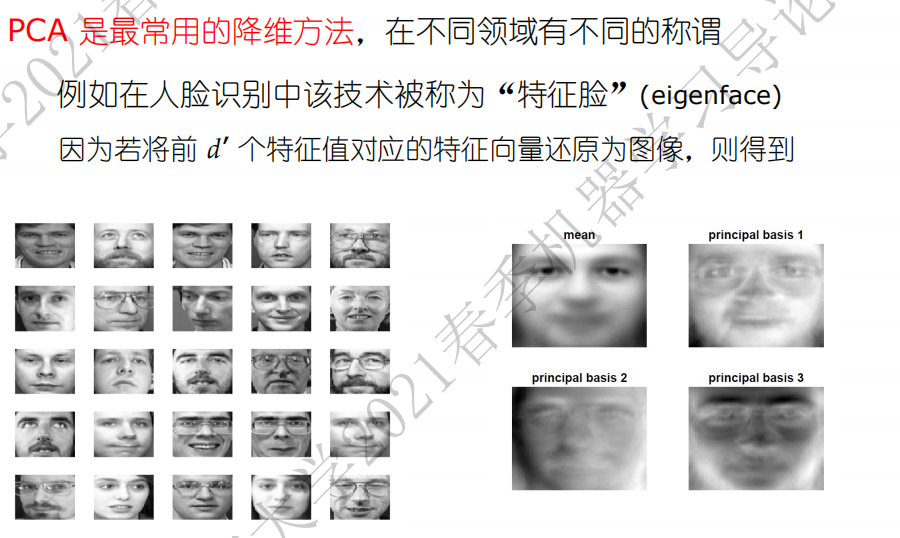
\[\dfrac{\sum_{i=1}^m\lambda_i}{\sum_{i=1}^n\lambda_i}\]人脸识别