引言
PID算法是一种比较常用的飞行控制算法,但实际上,PID算法思想能够应用在很多需要控制在稳态的系统中(比如温控)。本文我们尝试用举例和纯数学推导,来证明PID算法的合理性。
公式框架
作为控制算法,PID必然是应用在一个反馈系统中:
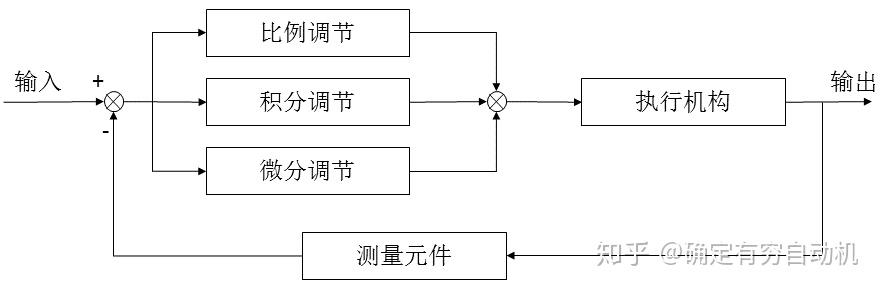
算法的特点是涉及到积分和微分:
\[U(t)=K_p(err(t)+\dfrac{1}{T_t}\int_0^t err(t)\mathrm{d}t+T_D\dfrac{\mathrm{d}err(t)}{\mathrm{d}t})\]总的来说,当得到系统的输出后,将输出经过比例,积分,微分3种运算方式,叠加到输入中,从而控制系统的行为,下面用一个简单的实例来说明。
水缸中的水和比例控制算法
假设有一个柱形水缸,其中水的高度是$h$,我们设置一个标准高度$H(h<H)$,我们不断向其中加水,目的是使水的高度最后维持在$h=H$的位置. 比例控制算法,也就是删去积分项和微分项的PID算法,其想法是随着$h$逐渐逼近$H$,加水的速度会逐渐减缓,我们可以有这样的关系:
\[\dfrac{\mathrm{d}h}{\mathrm{d}t}=k(H-h),k>0,h\in[0,H]\tag{1}\]为了问题的简洁,我们假设初始状态水缸中没有水,不难发现$(1)$式是一个微分方程:
\[\begin{aligned} \dfrac{\mathrm{d}h}{\mathrm{d}t}&=k(H-h)\\ \dfrac{\mathrm{d}h}{H-h}&=k\mathrm{d}t\\ \int\dfrac{\mathrm{d}h}{H-h}&=\int k\mathrm{d}t+C\\ -\ln(H-h)&=kt+C\\ h(t)&=H-Ce^{-kt} \end{aligned}\]所以$h$会随着时间推移逐渐收敛到$H$,这是在理想状态下一种平滑的维稳方式.
积分控制算法
但现实不会那么完美,假设水缸破了一个洞,水缸中的水会匀速从洞口流出,我们仍使用比例控制算法:
\[\dfrac{\mathrm{d}h}{\mathrm{d}t}=k(H-h)-v_{\text{out}}\tag{2}\]这里的$v_{\text{out}}$是单位时间里流失的水柱高度.
我们尝试求解这个微分方程:
\[\begin{aligned} \dfrac{\mathrm{d}h}{\mathrm{d}t}&=k(H-h)-v_{\text{out}}\\ \dfrac{\mathrm{d}h}{k(H-h)-v_{\text{out}}}&=\mathrm{dt}\\ \int\dfrac{\mathrm{d}h}{(H-\frac{v_{\text{out}}}{k})-h}&=\int k\mathrm{d}t\\ h(t)&=H-\dfrac{v_{\text{out}}}{k}-Ce^{-kt} \end{aligned}\]如果此时仍然坚持使用比例控制算法,那么水位最后只会收敛到$H-\dfrac{v_{out}}{k}$,而达不到要求,你或许会觉得水缸破洞是一件概率低的事情,但如果情景是一辆行驶中的汽车,如果想要他保持恒定的马力前进,可时刻存在一个恒定的阻力,使用比例控制算法也是不可行的,道理一样.
这里的$\dfrac{v_{\text{out}}}{k}$被称作“稳态误差”.
所以我们选择积分作为分量,加到我们的灌水速度上:
\[\dfrac{\mathrm{d}h}{\mathrm{d}t}=k_1(H-h)+k_2\int_0^t(H-h)\mathrm{d}t-v_{\text{out}}\tag{3}\]我们将这个微分积分混合式规范化为一个二阶线性微分方程:
\[\dfrac{\mathrm{d}^2h}{\mathrm{d}t^2}+k_1\dfrac{\mathrm{d}h}{\mathrm{d}t}+k_2h-k_2H=0\tag{4}\]由于冗余项$k_2H$是一个常数,设$h^\star$是微分方程
\[\dfrac{\mathrm{d}^2h}{\mathrm{d}t^2}+k_1\dfrac{\mathrm{d}h}{\mathrm{d}t}+k_2h=0\tag{5}\]的解,那么易于证明$(4)$的解就是$H+h^\star$. 我们来求解方程(5),其特征方程为:
\[\lambda^2+k_1\lambda+k_2=0\tag{6}\]为了使问题具有物理意义,我们必须要让$(6)$有两个实根:设$(6)$的两个解为$\lambda_1$和$\lambda_2$,则微分方程$(5)$的解为
\[h^\star(t)=C_1e^{\lambda_1t}+C_2e^{\lambda_2t}\tag{7}\]从而$(4)$的解就是
\[h(t)=H+C_1e^{\lambda_1t}+C_2e^{\lambda_2t}\tag{8}\]这里多出了参数$C_1,C_2,\lambda_1,\lambda_2$,它们的正负会影响$h(t)$的收敛性和收敛速度. 我们先来看$\lambda_i$. 基于一元二次方程,我们知道如下事实:
\[\lambda_1\lambda_2=k_2>0\\ \lambda_1+\lambda_2=-k_1<0\\\]$k_1$(比例控制参数)和$k_2$(积分控制参数)必须为正(否则无法保持稳定). 所以$\lambda_1$和$\lambda_2$皆负,不失一般性,设$\lambda_1<\lambda_2<0$.
再来看$C_i$,我们需要额外条件,因为设定了初态$h=0$,我们就可以有
\[\begin{aligned} h\vert_{t=0}&=0\\ \dfrac{\mathrm{d}h}{\mathrm{d}t}\vert_{t=0}&=m \end{aligned}\]这里我们使用线性代数的技巧:
\[\begin{bmatrix} 1&1\\ \lambda_1&\lambda_2\\ \end{bmatrix}\begin{bmatrix} C_1\\C_2 \end{bmatrix}=\begin{bmatrix} -H\\m \end{bmatrix}\]我们解得:
\[\begin{bmatrix} C_1\\\\C_2 \end{bmatrix}=\begin{bmatrix} \dfrac{m+\lambda_2H}{\lambda_1-\lambda_2}\\ \dfrac{m+\lambda_1H}{\lambda_2-\lambda_1}\\ \end{bmatrix}\tag{9}\]明显这里无法判断$C_1,C_2$正负性,关键就在于人为设置的参数$k_1,k_2$,这里我们更倾向于让$C_1,C_2$同号,从而拥有更快的收敛速度.
微分控制算法
换一个另外的例子,考虑刹车情况。平稳的驾驶车辆,当发现前面有红灯时,为了使得行车平稳,基本上提前几十米就放松油门并踩刹车了。当车辆离停车线非常近的时候,则使劲踩刹车,使车辆停下来。整个过程可以看做一个加入微分的控制策略。换到我们一直沿用的水缸的例子,那就是如果水位快到了($H-h<\varepsilon$),我们不想让它上升太快导致漫过$H$,那么就加入微分(导数)分量去控制这个系统:
\[\dfrac{\mathrm{d}h}{\mathrm{d}t}=k_1(H-h)+k_2\int_0^t(H-h)\mathrm{d}t+k_3\dfrac{\mathrm{d}}{\mathrm{d}t}(H-h)\tag{10}\]观察发现$(10)$仍然是一个二阶常系数微分方程:
\[(1+k_3)\dfrac{\mathrm{d}^2h}{\mathrm{d}t^2}+k_1\dfrac{\mathrm{d}h}{\mathrm{d}t}+k_2h-k_2H=0\tag{11}\]由于新增的微分项是误差对时间的导数,因为不断加水,误差减小,所以是负数,我们的目标是使得$\dfrac{\mathrm{d}h}{\mathrm{d}t}$变小,所以$k_3>0$.
遗憾的是,二阶线性微分方程的参数分析$(11)$难度过大,因此我们主动减小了分析问题的复杂度:将只采用比例控制算法和采用比例控制和微分控制两个算法的模型进行比较,我们来求解微分方程:
\[\dfrac{\mathrm{d}h}{\mathrm{d}t}=k(H-h)+\alpha\dfrac{\mathrm{d}}{\mathrm{d}t}(H-h)\tag{12}\]此处的$\alpha$就是上面的$k_3$,求解方法不再赘述,直接写解:
\[h=H-C\exp(-\dfrac{k}{1+\alpha}t)\]和$(1)$式的解作比较,发现$(12)$的解在收敛时更加平滑,所以我们从理论上证明了微分项存在的意义和正确性.
总结
和PID算法的标准式
\[U(t)=K_p(err(t)+\dfrac{1}{T_t}\int_0^t err(t)\mathrm{d}t+T_D\dfrac{\mathrm{d}err(t)}{\mathrm{d}t})\]相比,我们将其简化并转换成微分方程的求解,并验证了其比例项、积分项和微分项存在的正确性. 在《PID控制算法原理》中提到,在真正的工程实践中,最难的是确定三个项的系数,这就需要大量的实验以及经验来决定了。我们的工作正是为其提供了理论依据,或许可以减少尝试的数量(比如我们不会把$k_3$设置成负数).
下图是采用不同算法,系统的收敛性能图像:

其中的$P$曲线对应着”水缸漏水“的情景,$PID$曲线比$PI$曲线更稳定…这些结论都被我们一一证明.
$\text{Reference}$
- PID控制算法原理 https://zhuanlan.zhihu.com/p/39573490