问题概述
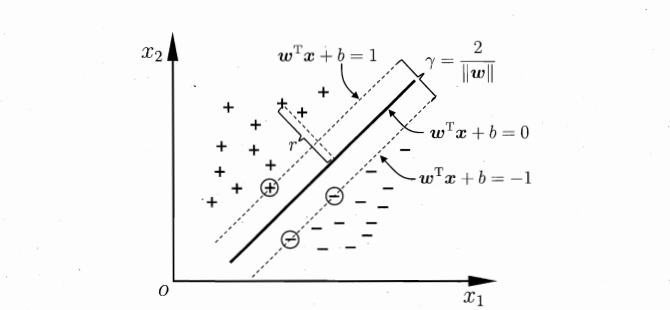
我们的目标就是
\[\begin{aligned} &\mathop{\max}\limits_{\pmb{w},{b}}\dfrac{2}{\|\pmb{w}\|}\\ &\text{s.t. }y_i(\pmb{w}^\top\pmb{x}_i+b)\ge1,i=1,2,...,m. \end{aligned}\tag{1}\]转换为最小化问题:
\[\begin{aligned} &\mathop{\min}\limits_{\pmb{w},{b}}\dfrac{1}{2}\|\pmb{w}\|^2\\ &\text{s.t. }y_i(\pmb{w}^\top\pmb{x}_i+b)\ge1,i=1,2,...,m. \end{aligned}\tag{2}\]对偶问题
我们使用拉格朗日乘子法得到其“对偶问题”:
\[\mathcal{L}(\pmb{w},b,\pmb{\lambda})=\dfrac{1}{2}\|\pmb{w}\|^2+\sum_{i=1}^m\lambda_i(1-y_i(\pmb{w}^\top\pmb{x}_i+b))\tag{3}\]其中$\pmb{\lambda}=(\lambda_1,\lambda_2,…,\lambda_m),\lambda_i\ge0$.
对变量求偏导:
\[\begin{cases} \dfrac{\partial}{\partial\pmb{w}}\mathcal{L}=\pmb{w}-\sum_{i=1}^m\lambda_iy_i\pmb{x}_i\\ \dfrac{\partial}{\partial b}\mathcal{L}=\sum_{i=1}^m\lambda_iy_i \end{cases}\tag{4}\]令上面两式为0:
\[\pmb{w}=\sum_{i=1}^m\lambda_iy_i\pmb{x}_i\tag{5}\] \[0=\sum_{i=1}^m\lambda_iy_i\tag{6}\]将$(4),(5)$带入$(3)$,则可消去变量:
\[\begin{aligned} \mathcal{L}(\pmb{w},b,\pmb{\lambda}) &=\dfrac{1}{2}\|\pmb{w}\|^2+\sum_{i=1}^m\lambda_i(1-y_i(\pmb{w}^\top\pmb{x}_i+b))\\ &=\dfrac{1}{2}(\sum_{i=1}^m\lambda_iy_i\pmb{x_i})^2+\sum_{i=1}^m\lambda_i-b\sum_{i=1}^m\lambda_iy_i-\sum_{i=1}^m\lambda_iy_i\pmb{w}^\top\pmb{x}_i\\ &=\dfrac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\lambda_i\lambda_jy_iy_j\pmb{x}_i^\top\pmb{x}_j-\sum_{i=1}^m\sum_{j=1}^m\lambda_i\lambda_jy_iy_j\pmb{x}_i^\top\pmb{x}_j+\sum_{i=1}^m\lambda_i\\ &=\sum_{i=1}^m\lambda_i-\dfrac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\lambda_i\lambda_jy_iy_j\pmb{x}_i^\top\pmb{x}_j \end{aligned}\]从而得到优化问题的对偶问题:
\[\mathop{\max}\limits_{\pmb{\lambda}}\sum_{i=1}^m\lambda_i-\dfrac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\lambda_i\lambda_jy_iy_j\pmb{x}_i^\top\pmb{x}_j\\ \text{s.t. }\sum_{i=1}^m\lambda_iy_i=0\\\lambda_i\ge0,i=1,2,...,m.\tag{7}\]解出$\pmb{\lambda}$后,我们就得到模型:
\[\begin{aligned} f(\pmb{x}) &=\pmb{w}^\top\pmb{x}+b\\ &=\sum_{i=1}^m\lambda_iy_i\pmb{x}_i^\top\pmb{x}+b \end{aligned}\]从对偶问题解出的$\lambda_i$式拉格朗日乘子,对应的是样本$(\pmb{x}_i,y_i)$,由于原问题有不等式约束,所以上述过程需满足$\text{KKT}$条件:
\[\begin{cases} \lambda_i\geq0;\\ y_if(\pmb{x}_i)-1\geq0\\ \lambda_i(y_if(\pmb{x}_i)-1)=0 \end{cases}\]$\text{KKT}$条件:定义拉格朗日函数:
\[\mathcal{L}(\pmb{x},\pmb{\lambda},\pmb{\mu})=f(\pmb{x})+\sum_{i=1}^m\lambda_ig_i(\pmb{x})+\sum_{j=1}^p\mu_kh_k(\pmb{x})\\\]$\text{KKT}$条件包括: \(\begin{cases} \nabla_{\pmb{x}}\mathcal{L}=0,\\ g_i(\pmb{x})=0,i=1,...,m.\\ h_j(\pmb{x})\leq0,\\ \mu_j\geq0\\ \mu_jh_j(\pmb{x})=0,j=1,...,p. \end{cases}\)
于是,对于任意训练样本$(\pmb{x_i},y_i)$,总有$\lambda_i=0$或$y_if(x_i)=1$. $\lambda_i=0$的点不会对$f(\pmb{x})$有任何影响,否则样本点都在最大间隔边界上,是一个支持向量. 这为我们的训练带来启示,即大部分样本都不需要,最终模型只与支持向量有关.
SMO算法
那么我们如何求解$(7)$式?$\text{SMO}$算法是求解该二次规划问题的代表.